Here, we present you the Editorial for the Virtual Farewell IIT (ISM). I hope you enjoyed the contest !!
A. Farewell or Best Wishes
Author : chefpr7
Firstly, if the office is located anywhere in the path of the auto, then their plan will always fail, i.e if $$$X=1$$$ or $$$Y=M$$$ then best wishes are on the way.
Otherwise, the auto can meet the agents only in the cells ($$$1$$$, $$$Y$$$) or ($$$X$$$, $$$M$$$). The time needed to reach these cells can be obtained in $$$O$$$($$$1$$$).
Agent A initially headed North reaches the cell ($$$1$$$, $$$Y$$$) at time $$$t$$$ = $$$Y$$$-$$$1$$$ and after that it comes back at intervals of $$$2*(N-1)$$$. So all we need to do is check whether the time taken by the auto to reach any of the two cells is a term in the arithmetic progression of time taken by an agent to reach that cell. If we check this for all the agents, and the auto clashes with none, then "Farewell" else "BestWishes".
The overall complexity is $$$O$$$($$$1$$$) per test case.
#include<bits/stdc++.h>
using namespace std;
#define int long long
void solve()
{
int n,m,x,y;
cin>>n>>m>>x>>y;
bool flag=true;
// Let flag indicate the success of farewell trip
if(x==1&&y==1)
{
flag=false;
}
if(x==1||y==m)
{
flag=false;
}
int reach1 = y - 1; // time for auto to reach cell (1,Y)
int reach2 = m - 1 + x - 1; // time for auto to reach cell (X,M)
int a,d;
//AP-1
a = x - 1;
d = 2*(n-1);
// reach1 = a + (t-1)*d
if((reach1-a)>=0&&(reach1-a)%d==0)
{
flag=false;
}
//AP-2
a = n-x+n-1;
d = 2*(n-1);
if((reach1-a)>=0&&(reach1-a)%d==0)
{
flag=false;
}
//AP-3
a = m - y;
d = 2*(m-1);
if((reach2-a)>=0&&(reach2-a)%d==0)
{
flag=false;
}
//AP-4
a = y - 1 + m - 1 ;
d = 2*(m-1);
if((reach2-a)>=0&&(reach2-a)%d==0)
{
flag=false;
}
if(flag)
cout<<"Farewell"<<'\n';
else
cout<<"BestWishes"<<'\n';
}
int32_t main()
{
int t;
cin>>t;
for(int i=1;i<=t;i++)
solve();
return 0;
}
B. Amber Kand
Author : thenainesh
For a string t, consider two sub-sequences :
$$$S = s_1, s_2, s_3, ... s_p$$$
$$$J = j_1, j_2, j_3, ... j_q$$$
where $$$s_1$$$ is the first character liked by seniors in string $$$t$$$, $$$s_2$$$ is the second character liked by seniors, and so on and $$$j_1$$$ is the first character liked by juniors in string $$$t$$$, $$$j_2$$$ is the second character liked by juniors, and so on.
As two adjacent characters (such that both of them are liked by either seniors or juniors) can never be swapped, the sub-sequences $$$S$$$ and $$$J$$$ of string $$$t$$$ can never be changed by any number of adjacent swappings.
If the corresponding sub-sequences $$$S$$$ and $$$J$$$ of Special String are equal to that of Elegant String, the former can be transformed into the latter.
#include<bits/stdc++.h>
using namespace std;
int main()
{
string s,t;
cin>>s;
cin>>t;
string a,b,c,d;
for(auto ch : s)
if ( (ch-'a') % 2 == 0 ) a.push_back( ch );
else b.push_back(ch);
for(auto ch : t)
if ( ( ch -'a') % 2 == 0 ) c.push_back( ch );
else d.push_back( ch );
if (a==c && b == d) cout<<"Yes";
else cout<<"No";
}
C. Matiyao Be Mid Sem hee toh hai
Author : Sanket_17
Suppose that you want to replace the subject marks $$$X$$$ by some marks $$$Y$$$. Then, it is best to choose $$$X$$$, as small as possible and $$$Y$$$, as large as possible. So, sort the array $$$A$$$ in non-decreasing order i.e. $$$A_1 \leq A_2 \leq ... \leq A_N$$$. Note that the order in which we perform the operation does not alter the answer. Because it rewrites the same subject marks more than once, which is absolutely useless. So, sort the array of pairs $$$<C[i], B[i]>$$$ in non-increasing order of $$$C[i]$$$ ( If C[i]s are equal, arrange in non-increasing order of B[i]s ).
Now, take the highest $$$C[i]$$$ and use it until array ends or an array element greater than $$$C[i]$$$ is found or we have used $$$m$$$ operations, whichever is earlier. The solution has a time complexity of O($$$MlogM + NlogN$$$). You can refer to the solution for a better understanding.
#include <bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define endl "\n"
#define int long long
const int N = 1e5 + 5;
int n, m, ans = 0;
int a[N], b[N], c[N];
vector<pair<int, int> > v;
int32_t main()
{
IOS;
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> a[i];
for(int i = 1; i <= m; i++)
{
cin >> b[i] >> c[i];
v.push_back({c[i], b[i]});
}
sort(v.rbegin(), v.rend());
sort(a + 1, a + n + 1);
int idx = 0;
for(int i = 1; i <= n; i++)
{
if(idx >= m)
ans += a[i];
else
{
ans += max(a[i], v[idx].first);
v[idx].second--;
if(v[idx].second == 0)
idx++;
}
}
cout << ans;
return 0;
}
D. Best Wishes !!
Author : cjchirag7
The problem can be solved easily by dynamic programming as follows:
Let $$$dp[i]$$$ denote the minimum number of days to make the charges for a single day, equal to $$$i$$$.
Clearly, $$$dp[1]$$$ = 1 ( Since, the initial charges on day 1 is Rs. 1 itself )
Now, $$$dp[i]$$$ can be computed by means of the following recurrence relation :
$$$dp[i]$$$ = $$$1 + min(dp[\frac{i}{2}],dp[\frac{i}{3}],dp[i-1])$$$
( You need to consider $$$dp[\frac{i}{2}]$$$ only when $$$i$$$ is divisible by 2 and $$$dp[\frac{i}{3}]$$$ only when $$$i$$$ is divisible by 3 )
So, just precompute $$$dp[i]$$$ for $$$i = 1,2,3 ... ,1000000$$$.
Now, for each query amount Rs. $$$D$$$, you can simply output $$$dp[D]$$$ as the minimum number of days.
The sequence of amounts can be easily computed by traceback of this $$$dp$$$ table. Try it yourself and if you don't get it, just look at the solution below.
#include <bits/stdc++.h>
using namespace std;
const int MAX=1000000; //Maximum value of D can be 10^6
int main() {
int t;
cin>>t;
vector<int> dp(MAX+1,INT_MAX); // initialise dp[i] with INT_MAX
// Here dp[i] = min. number of days to make the charges i on a single day.
dp[1]=1; // Initial charge is Rs. 1, so no extra days required
for(int i=2; i<=MAX; i++)
{
if(i%2==0)
{
dp[i]=min(dp[i],dp[i/2]+1);
}
if(i%3==0)
{
dp[i]=min(dp[i],dp[i/3]+1);
}
if(i-1>=1)
{
dp[i]=min(dp[i],dp[i-1]+1);
}
}
while(t--)
{
int n;
cin>>n;
cout<<dp[n]<<'\n'; // minimum number of days to make the charges for a single day, equal to n
vector<int> seq;
// Now, perform a traceback to get the sequence of charges on each day.
for(int i=n; i>1;)
{
seq.push_back(i);
if(i-1>=1&&dp[i]==1+dp[i-1])
{
i=i-1;
}
else if(i%2==0&&dp[i]==1+dp[i/2])
{
i=i/2;
}
else if(i%3==0&&dp[i]==1+dp[i/3])
{
i=i/3;
}
}
seq.push_back(1);
reverse(seq.begin(),seq.end());
for(int i=0; i<(int)seq.size(); i++)
{
cout<<seq[i]<<" ";
}
cout<<'\n';
}
return 0;
}
E. Dictator's plan for Valentine's day!
Author : will.earn.you
All $$$N$$$ couples will start moving at integer time, so the time interval $$$[L_i-z,R_i-z)$$$ can be regarded as a time interval $$$[L_i,R_i)$$$ (for simplicity).
The $$$i^{th}$$$ Guard does his duty at coordinate $$$X_i$$$ during $$$[L_i,R_i)$$$. Then it holds that only those couples who start the coordinate $$$0$$$ during time $$$[L_i−X_i,R_i−X_i)$$$ could be affected by this Guard (those who didn't start during this interval would never face this Guard).
If you try to judge for each of the $$$N$$$ couples, whether the $$$M$$$ Guards affect them or not, then the time complexity would be $$$O(N*M)$$$ which would result in $$$TLE$$$. Instead, you can use $$$sorting$$$ and $$$Binary-Search$$$.
Now create a vector of tuple of $$$(X_i, L_i−X_i, R_i−X_i)$$$ and sort it in non-decreasing order of $$$x-coordinate$$$.
Note that the starting time of all couples is distinct and hence this makes our problem simple. Since we have sorted our vector in non-decreasing order of their $$$x-coordinate$$$ so when iterating from $$$i = 1$$$ to $$$M$$$, we will always try to find how many couples would be caught by this particular $$$Guard$$$ and those couples who still have not been caught by any $$$Guard$$$ and starting time lies during $$$[L_i−X_i, R_i−X_i)$$$ will be caught by this guard and we find this by using $$$Binary-Search$$$.
Following this approach, you can sort in O( $$$NlogN$$$ ), look for the minimum value in O( $$$logN$$$ ) for each $$$M$$$ Guard using binary search ( you can use lower_bound function in C++ too), so you can solve this problem in O( $$$(N+M)logN$$$ ) overall.
#include<bits/stdc++.h>
using namespace std;
int main(){
int M,N;
scanf("%d%d",&M,&N);
vector<tuple<int,int,int>> vec;
for(int i=0;i<M;i++){
int l,r,x;
scanf("%d%d%d",&l,&r,&x);
vec.emplace_back(x,l-x,r-x);
}
vector<int> Time(N);
set<int> st;
for(int i=0;i<N;i++){
scanf("%d",&Time[i]);
st.insert(Time[i]);
}
// Remember All the time of the couple are distinct and are in increasing order......
sort(vec.begin(),vec.end());
map<int,int> ans;
for(int i=0;i<M;i++){
int cor=get<0>(vec[i]), l=get<1>(vec[i]), r=get<2>(vec[i]);
auto it1=st.lower_bound(l);
auto it2=st.lower_bound(r);
vector<int> done;
while(it1!=it2){
ans[*it1]=cor;
done.push_back(*it1);
it1++;
}
for(int x : done) st.erase(x);
}
for(int i=0;i<N;i++){
if(ans.count(Time[i])) cout<<ans[Time[i]]<<endl;
else cout<<"-1"<<endl;
}
return 0;
}
F. Basant and the Master Plan
Author : Hypnos
The problem can be solved by many other methods. But I will discuss the simplest one here. Since, the required perfect number should be made only from the digits a, b, c, there can be total $$$3^{9} \approx 20,000$$$ such 9-digit numbers. Similarly, we can have $$$3^{8}$$$ such 8-digit numbers and so on. (We don't consider the number $$$10^9$$$, as it can't be a perfect number). So, we can simply check for each of these numbers (easily using recursion), whether it is a perfect number. And in this way, push all the $$$unique$$$ perfect numbers in a vector $$$roses$$$.
Now, the question arises how can we check whether a number $$$X$$$ is a perfect number, efficiently? Let the sum of digits of $$$X$$$ be $$$sum$$$ and its number of digits be $$$len$$$. Then, for $$$X$$$ to be a perfect number, either of the digits $$$a$$$, $$$b$$$ or $$$c$$$ (if present in the number) should be the average of all the other digits. Suppose, we want to check this for $$$a$$$. This, means we want to check whether $$$\frac{(sum-a)}{(len-1)} = a$$$ or $$$sum-a = (len-1)\cdot a$$$, which can be done in O(1).
Once, we have the vector $$$roses$$$ with all the perfect numbers made up of the digits $$$a$$$, $$$b$$$, $$$c$$$, we can sort it, so as to easily get the number of roses between $$$L$$$ and $$$R$$$ by using $$$binary-search$$$ ( you may also use lower_bound and upper_bound in C++, for this ). Now, just simply output the shop no. of the shop with the maximum number of perfect roses :)
#include <bits/stdc++.h>
#define int long long
using namespace std;
int l,r;
int a,b,c;
vector<int> roses;
bool perfect(int num)
{
int sum=0;
int len=0;
bool ap,bp,cp;
// The variables represent whether the digits a, b, c, are present in num
ap=bp=cp=false;
while(num>0)
{
if(num%10==a)
ap=true;
if(num%10==b)
bp=true;
if(num%10==c)
cp=true;
sum+=(num%10); // sum of digits
len++; // number of digits
num=num/10;
}
if(len<=1)
return false; // since, 1-digit numbers are not perfect
if(ap&&(sum-a)==a*(len-1))
{
return true; // if a is the average of other digits
}
if(bp&&(sum-b)==b*(len-1))
{
return true; // if b is the average of other digits
}
if(cp&&(sum-c)==c*(len-1))
{
return true; // if c is the average of other digits
}
// otherwise not a perfect number
return false;
}
void solve(int num)
{
// l=1 and r=1e9
if(num>r)
return;
if(num>=l&&num<=r&&perfect(num))
{
roses.push_back(num);
}
if(num*10+a<=r&&num*10+a!=num)
solve(num*10+a);
if(num*10+b<=r&&num*10+b!=num)
solve(num*10+b);
if(num*10+c<=r&&num*10+c!=num)
solve(num*10+c);
}
int32_t main() {
int q;
cin>>a>>b>>c>>q;
int mx=0;
int ans=1;
l=1;
r=1e9;
solve(0);
sort(roses.begin(),roses.end());
int len=unique(roses.begin(),roses.end())-roses.begin(); // remove duplicates
for(int i=0; i<q; i++)
{
int cnt=0;
cin>>l>>r;
int lpos=lower_bound(roses.begin(),roses.begin()+len,l)-roses.begin();
int upos=upper_bound(roses.begin(),roses.begin()+len,r)-roses.begin();
cnt=upos-lpos; // Number of perfect roses in the closed interval [L,R]
if(cnt>mx)
{
// update ans and mx
mx=cnt;
ans=i+1;
}
}
cout<<ans<<'\n';
return 0;
}
G. Secret Society and a Certain Someone
Author : rath772k
Let's rephrase the question in simpler terms. It is obvious that offices are nodes, passages are edges, and security levels are weights of the edges. Also, our graph is a tree, so the shortest paths are unique between any two nodes. We have to find for each edge $$$e$$$, the number of times it is the edge with the highest weight for all shortest paths from $$$u$$$ to $$$v$$$ with $$$e$$$ in the path, let it be $$$cnt_e$$$. And among all the edges we have to find those edge $$$e$$$ such that $$$cnt_e$$$ is maximum.
Let's solve a simpler version of the problem where all the edges have distinct weights. Consider an edge $$$e$$$, let it be the edge with maximum weight. It is easy to see that it is the edge with maximum weight for all the paths that have this edge. How many such paths are there ( or what is $$$cnt_e$$$ )?
Let's denote the shortest path from node $$$u$$$ to node $$$v$$$ as $$$u--v$$$, then $$$cnt_e$$$ is simply the product of the number of nodes that can reach $$$e$$$ from one side of $$$e$$$ and the number of nodes from the other side. Note that in our question, $$$u--v$$$ and $$$v--u$$$ are different and since $$$u$$$ $$$\neq$$$ $$$v$$$, we have to count the previous step twice. But this is the answer only for the edge with maximum weight. What about the others? We'll consider the edges in increasing order of weights, and for every edge we consider, that'll be the edge with maximum weight so far. For the considered edge say $$$e$$$, $$$cnt_e$$$ is just the product of the size of connected components of its endpoints before adding this edge between them. This can be done with DSU.
The transition from this simpler version to our original question is simple. We'll consider the edges in non-decreasing order, but consider all the edges with equal weights together. When the considered edges are equal, calculating $$$cnt_e$$$ becomes a little tricky as the endpoints of the considered edge may not be in one of the connected components of the graph constructed so far. Thus for this, we make a DFS traversal of a temporary graph with edges as the current equal edges and nodes as the connected component to which each endpoint belongs to. After making the graph (which will be a forest), let's calculate the size of each tree of the forest (size of each node is the size of its connected component). For one of the equal edges $$$e1$$$ that connects nodes $$$u$$$ and $$$v$$$, $$$cnt_{e1}$$$ is product of size of subtree $$$u$$$ and (size of the whole tree $$$-$$$ size of subtree $$$u$$$). This can be easily computed with DFS.
#include <bits/stdc++.h>
using namespace std;
vector<int> adj[200009];
int par[200009],sz[200009];
int fin(int v)
{
if(par[v]==v)
return v;
return par[v] = fin(par[v]);
}
void uni(int a, int b)
{
a=fin(a);
b=fin(b);
if(a==b) return;
if(sz[a]<sz[b])
swap(a,b);
par[b]=a;
sz[a] += sz[b];
}
struct edge
{
int a,b,c,d;
};
vector<edge> e;
bool cmp(edge A, edge B)
{
return A.c < B.c;
}
int dp[200009],root[200009];
void dfs(int v)
{
dp[v] = sz[fin(v)];
for(auto u:adj[v])
{
if(!root[u])
{
root[u]=root[v];
dfs(u);
dp[v] += dp[u];
}
}
}
void solve()
{
int n,i,j,k;
cin>>n;
e.resize(n);
for(i=1;i<n;i++)
{
cin>>e[i].a;
cin>>e[i].b;
cin>>e[i].c;
e[i].d=i;
sz[i]=1;
par[i]=i;
}
sz[n]=1;
par[n]=n;
sort(e.begin()+1,e.end(),cmp);
long long ans =0,temp;
vector<int> v;
for(i=1,j=1;i<n;i=j)
{
while(j<n && e[i].c == e[j].c) j++;
for(k=i;k<j;k++)
{
e[k].a=fin(e[k].a);
e[k].b=fin(e[k].b);
adj[e[k].a].push_back(e[k].b);
adj[e[k].b].push_back(e[k].a);
root[e[k].b]=root[e[k].a]=0;
}
for(k=i;k<j;k++)
{
if(!root[e[k].a])
{
root[e[k].a] = e[k].a;
dfs(e[k].a);
}
}
for(k=i;k<j;k++)
{
long long small = min(dp[e[k].a], dp[e[k].b]);
long long large = dp[root[e[k].a]];
temp = small * (large-small);
if(temp>ans)
{
ans=temp;
v.clear();
v.push_back(e[k].d);
}
else if(temp==ans)
{
v.push_back(e[k].d);
}
}
for(k=i;k<j;k++)
{
adj[e[k].a].clear();
adj[e[k].b].clear();
uni(e[k].a,e[k].b);
}
}
ans <<= 1;
sort(v.begin(),v.end());
cout<<ans<<' '<<v.size()<<'\n';
for(auto u:v)
cout<<u<<' ';
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
solve();
}
H. Ye Wali Meri Hai!!
Author : ujju_sucks
The problem simply reduces to find the maximum element in the sub-tree of $$$s_1$$$ excluding $$$s_1$$$ and the sub-trees of $$$s_2$$$ to $$$s_k$$$
For this, we will have to convert the tree into a tree array. We can do this using DFS traversal and store the nodes in the array in the order, they are visited.
For learning more about this, check here
We will also need to store the size of the sub-tree for each node.
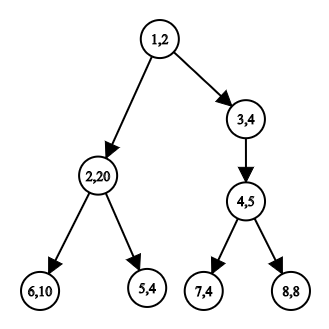
Let $$$index[node]$$$ store the order in their dfs. In the given tree, $$$index[1] = 0$$$ and $$$valueAt[0] = 1$$$, $$$index[2] = 1$$$ and $$$valueAt[1] = 2$$$, $$$index[6] = 2$$$ and $$$valueAt[2] = 6$$$, $$$index[5] = 3$$$ and $$$valueAt[3] = 5$$$,$$$index[3] = 4$$$ and $$$valueAt[4] = 3$$$ and so on..
If $$$index[node1] < index[node2]$$$ and $$$index[node2]+subtree[node2] \leq index[node1]+ subtree[node1]$$$ , it means that node-2 lies in the sub-tree of node-1. Else node-1 and node-2 are un-related.
First, we will check if $$$s_1$$$ lies in the subtree of $$$s_2$$$ to $$$s_k$$$. If yes, print -1.
Now, we will need to create a query max segment tree that stores the weights in the order of the tree array.
For the given example, weights are stored in segment tree as $$$weight[valueAt[0]]$$$ to $$$weight[valueAt[n-1]]$$$ in the order. Think about it.
Now, We will iterate from $$$i = 2$$$ to $$$k$$$, if $$$s_1$$$ and $$$s_i$$$ are related, we will calculate the maximum in the segment between them using the concept of $$$two-pointers$$$. Again, Think about it :-)
For Example , If queried, $$$s_1 = 1$$$ and $$$s_2 = 7$$$, our segments will be $$$(valueAt[1]+1,valueAt[7]-1)$$$ and $$$(valueAt[7]+1,n-1)$$$
#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
#define maxn 200005
typedef pair<ll,ll> pll;
typedef pair<int,int> pint;
#define pb push_back
#define fi first
#define mkp make_pair
#define se second
#define rep(i,n) for(ll i=0;i<n;i++)
#define repeat(i,start,n) for(ll i=start;i<n;i++)
ll Tree[400001];
// Segment tree for storing the maximum in a given segment
void build_max(int node,int start,int end,int a[],int valueAt[]){
if(start==end){
Tree[node]=a[valueAt[start]]; // order: weight[valueAt[0]] to weight[valueAt[n-1]]
return;
}
int mid=((start+end)>>1);
build_max(2*node+1,start,mid,a,valueAt);
build_max(2*node+2,mid+1,end,a,valueAt);
Tree[node]=max(Tree[2*node+1],Tree[2*node+2]);
}
ll query_max(int node,int start,int end,int l,int r){
if(start>end||end<l||start>r)
return -1; // If out of bound, return -1;
if(start>=l&&end<=r)
return(Tree[node]);
int mid = (start+end)/2 ;
ll p1 = query_max(node*2+1, start, mid, l,r);
ll p2 = query_max(node*2+2, mid+1, end , l,r);
return max(p1,p2);
}
int sub[100001];
int index[100001];
int valueAt[100001];
int t;
int n;
vector<int> adj[100001];
void dfs1(int i,int p){
index[i]=t; // order of nodes in dfs
valueAt[t]=i; //valueAt a given index in tree array
t++;
sub[i]=1;
rep(j,adj[i].size()){
if(adj[i][j]==p)
continue;
dfs1(adj[i][j],i);
sub[i]+=sub[adj[i][j]]; // length of sub-tree
}
}
void solve(){
int q;
scanf("%d%d",&n,&q);
int a[n];
rep(i,n)
scanf("%lld",&a[i]);
rep(i,n-1){
int x,y;
scanf("%d%d",&x,&y);
x--,y--;
adj[x].pb(y);
adj[y].pb(x);
}
dfs1(0,-1);
build_max(0,0,n-1,a,valueAt);
while(q--){
vector<pint> v;
int k;
scanf("%d",&k);
int a1[k];
rep(i,k){
scanf("%d",&a1[i]);
a1[i]--;
}
int t=0;
if(sub[a1[0]]==1){
printf("-1\n");
continue;
}
repeat(i,1,k){
//Checking if s1 lies inside any of s2 to sk
if(index[a1[i]]<index[a1[0]]&&index[a1[i]]+sub[a1[i]]>=index[a1[0]]+sub[a1[0]]){
printf("-1\n");
t=1;
break;
}
// If s1 and s_i are unrelated, continue;
if(index[a1[i]]+sub[a1[i]]-1<index[a1[0]])
continue;
if(index[a1[i]]>index[a1[0]]+sub[a1[0]]-1)
continue;
v.pb({index[a1[i]],index[a1[i]]+sub[a1[i]]-1}); // (Index of node in array,Index of last element in sub-tree of node in array)
}
if(t==1)
continue;
sort(v.begin(),v.end());
int u[max(1,(int)v.size())]={0};
rep(i,v.size()){
int j=i+1;
while(j<v.size()&&v[j].se<=v[i].se){
u[j]=1; // excluding the nodes which are a part of other given nodes
j++;
}
i=j-1;
}
int ans=-1;
int prev=index[a1[0]]+1; //seting pointer for the beginning of node
rep(i,v.size()){
while(i<v.size()&&u[i]==1)
i++;
if(i==v.size())
break;
if(prev>v[i].fi-1){
prev=v[i].se+1; // moving the pointer to the next unvisited node of the sub-tree of s1
continue;
}
ans=max(ans,(int)query_max(0,0,n-1,prev,(int)v[i].fi-1)); // querying in the sub-segments formed
prev=v[i].se+1; // moving the pointer to the next unvisited node of the sub-tree of s1
}
if(prev<=index[a1[0]]+sub[a1[0]]-1)
ans=max(ans,(int)query_max(0,0,n-1,prev,index[a1[0]]+sub[a1[0]]-1));
printf("%d\n",ans);
}
}
int main(){
solve();
}
I. Treat To Banta Hai
Author : Its_Easy
We'll solve the problem using the convex hull trick. You can learn it from here if you don't know it.
Lets compute "special prefix" array as $$$spre[i]=spre[i-1]+i*s[i]$$$ .Also maintain a prefix sum array $$$pre[i]=pre[i-1]+s[i]$$$ .Now since we want to find the best subarray $$$(l,r]$$$ (observe the opening bracket in '$$$l$$$' , this is to simplify the equations we'll get) to maximize the happiness score. The strategy would be to iterate over all possible '$$$r$$$' and find the best '$$$l$$$' in the range $$$[1,r-1]$$$ for every $$$r$$$. Simple, right? But there arises two problems — $$$1^{st}$$$ is the transition — if we iterate over all possible '$$$l$$$' for a corresponding '$$$r$$$', what value we want and what we have in $$$spre[i]$$$ is different ,$$$2^{nd}$$$ is the time complexity would still be O($$$n^2$$$).
Lets solve the $$$1^{st}$$$ problem. "The transition" — suppose we want our happiness score in the range $$$(3,5]$$$ , so what's required is $$$1*s_3+2*s_4+3*s_5$$$ .Lets observe what we have in $$$spre[r] = spre[5] = 1*s_1+2*s_2+3*s_3+4*s_4+5*s_5$$$ and $$$spre[l] = spre[3] = 1*s_1+2*s_2+3*s_3$$$ and what we require is $$$1*s_4+2*s_5$$$. Did you observe?
$$$spre[r]-spre[l]-(pre[r]-pre[l])*l$$$ =happiness score in the range $$$(l,r]$$$.You will easily get it, once you write it on a piece of paper.
Now,lets solve the $$$2^{nd}$$$ problem. "Reducing the time complexity" — Now clearly seeing the constraints, O($$$n^2$$$) won't work. Here comes the use of convex hull trick. For every '$$$r$$$' ,we want an '$$$l$$$' before it. So ,first lets see what should be the line equation which we are going to exploit. As we have seen, for all $$$x$$$ in $$$[1,r]$$$,we will find the $$$i$$$ in the range $$$[1,x-1]$$$ for the best score to be maximum :
$$$spre[x]-spre[i]-(pre[x]-pre[i])*i$$$ $$$= spre[x]-spre[i]-pre[x]*i+pre[i]*i$$$ $$$= i*(-pre[x])+pre[i]*i-spre[i]+(spre[x])$$$
So ,the line which we get depending on previous values is:
$$$y=m* x + c$$$ $$$=i*(-pre[x]) +(pre[i]*i-spre[i])$$$
($$$spre[x]$$$ is not dependent on previous values so we can add it after getting the result)
So that's it. We have achieved O($$$nlogn$$$) using this trick. After getting the equation of the line, it's just a work of few lines of code in the implementation of convex hull trick, if you have the template ready :)
The code is given below, for reference.
#include<bits/stdc++.h>
#define eb emplace_back
#define pb push_back
#define size(s) (int)s.size()
#define int long long
#define vi vector<int>
#define all(v) (v).begin(),(v).end()
using namespace std;
template<class T>
T abst(T a)
{return a<0?-a:a;}
template<class T>
T max2(T a,T b){return a>b?a:b;}
template<class T>
T min2(T a,T b){return a<b?a:b;}
const int INF=1e15;
struct line
{
int m,b;
};
double intersect(line x,line y)
{
if(x.m==y.m) return INF;
return (double)(y.b-x.b)/(double)(x.m-y.m);
}
vector<line> st;
vector<long double> points;
int eval(int x,line y)
{
return x*y.m+y.b;
}
void addline(line x)
{
if(st.empty())
{
st.pb(x);
return;
}
if(size(st)==1)
{
points.pb(intersect(x,st[0]));
st.pb(x);
return;
}
while(size(points))
{
line l1=st.back();
st.pop_back();
if(intersect(x,st.back())<=points.back())
{
points.pop_back();
}
else
{
st.pb(l1);
break;
}
}
points.pb(intersect(x,st.back()));
st.pb(x);
}
int findbest(int x)
{
int ind=lower_bound(all(points),x)-points.begin();
return eval(x,st[ind]);
}
vi arr(200005),spre(200005),pre(200005);
void solve()
{
int n;cin>>n;
for(int i=1;i<=n;i++)
{
cin>>arr[i];
spre[i]=spre[i-1]+i*arr[i];
pre[i]=pre[i-1]+arr[i];
}
int ans=0;
line l;
l.m=l.b=0;
addline(l);
for(int i=1;i<=n;i++)
{
ans=max2(ans,findbest(-pre[i])+spre[i]);
l.m=i;
l.b=i*pre[i]-spre[i];
addline(l);
}
cout<<ans;
}
int32_t main(){
solve();
}
J. RD Bhaiya and his new token system
Author : cjchirag7
We can easily solve the problem by assuming the numbers to be vectors in $$$k$$$-dimensional space over field $$$\mathbb{Z}_2$$$ of residues modulo 2, where k is the maximum possible number of bits in the numbers. In our problem, $$$k=30$$$.
Then, it can be proven that xor of some of these numbers is equivalent to the addition of the corresponding vectors in the vector space. Knowing the properties of XOR and vector space, we can easily find the basis of a given set of numbers in O( $$$n \cdot k$$$ ), where $$$n$$$ is the size of the set of the numbers. But in the given problem, we need to use an online version of this algorithm, as there can be many $$$type-2$$$ queries in between 2 $$$type-1$$$ queries. If you don't know the algorithm, you can see the code below, for reference.
Once we have the vector $$$basis$$$ such that $$$basis[i]$$$ keeps the mask of a number whose last set position in the binary vector representation is $$$i$$$, we can answer the queries of the second type in the following way -
Note that any instant, if the size of the set of basis vectors is $$$sz$$$, we would have $$$total = 2^{sz}$$$ unique token numbers. We initialise $$$ans=0$$$ and start iterating the basis vectors from $$$i=29$$$ to $$$i=0$$$.For the first iteration, if $$$n \leq \frac{tot}{2}$$$ , then we will set the $$$i^{th}$$$ bit to 0. Otherwise, we set it to 1 and subtract $$$\frac{tot}{2}$$$ from n. Next, we move on to the next basis vector and continue. In the end, $$$n$$$ will be 1 and we'll get our answer by setting 0 in $$$ans$$$ for the remaining lower bits. The solution is given below.
#include <bits/stdc++.h>
using namespace std;
int basis[30]; // basis[i]= basis which has MSB = i
int sz=0;
void insertVector(int num)
{
for(int i=29; i>=0; i--)
{
if((num&(1<<i))==0)
continue;
if(basis[i]==0)
{
basis[i]=num;
sz++;
}
num=num^basis[i];
}
}
int32_t main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int q;
cin>>q;
while(q--)
{
int p,n;
cin>>p>>n;
if(p==1)
{
insertVector(n);
}
else
{
int ans=0;
int tot=1<<sz;
for(int i=29; i>=0; i--)
{
if(basis[i])
{
if((n<=tot/2&&(ans&(1<<i)))||(n>tot/2&&(ans&(1<<i))==0))
{
ans^=basis[i];
}
if(n>tot/2)
{
n=n-tot/2;
}
tot=tot/2;
}
}
cout<<ans<<'\n';
}
}
return 0;
}
Feedbacks are welcome !










