Для каждого символа посчитаем, в какую сторону выгоднее вращать диск. Это можно сделать либо формулой: min(abs(a[i] - b[i]), 10 - abs(a[i] - b[i])), либо даже двумя циклами for: в прямом или обратном направлении.
Посчитаем количество оценок, меньших y. Если таких больше 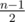 штук, то мы не сможем удовлетворить второму условию (про медиану), и ответ -1. Иначе получим ровно столько оценок y, чтобы количество оценок, больших или равных y, было как минимум
штук, то мы не сможем удовлетворить второму условию (про медиану), и ответ -1. Иначе получим ровно столько оценок y, чтобы количество оценок, больших или равных y, было как минимум 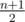 штук (возможно, это уже выполняется). Это минимальное необходимое действие для удовлетворения второго условия.
штук (возможно, это уже выполняется). Это минимальное необходимое действие для удовлетворения второго условия.
Теперь, чтобы не нарушить первое условие, сделаем оставшиеся неизвестные оценки как можно меньше — единицами, и проверим сумму. Если она больше x, то ответ снова -1, иначе требуемые оценки найдены.
Я выделил здесь три случая, хотя некоторые из них можно объединить.
- Если начальная и конечная клетка совпадают, посмотрим на количество целых соседей этой клетки. Если есть хотя бы один целый сосед, то пойдем туда и сразу же вернемся обратно, выполнив задачу — в этом случае ответ YES.
- Если начальная и конечная клетка являются соседями, то посмотрим на тип конечной клетки. Если конечная клетка треснувшая, то ответ YES. Иначе для положительного ответа необходимо, чтобы у нее был хотя бы один целый сосед — пойдем на конечную клетку, затем на этого целого соседа, а потом вернемся обратно.
- В наиболее общем случае проверим, существует ли путь по целым клеткам от начальной клетки до конечной. Если нет, то ответ NO. Иначе посмотрим на тип конечной клетки. Если она целая, то для существования ответа необходимо наличие у нее двух целых соседей — по одному мы придем в нее, а второй используем как промежуточную точку, а если конечная клетка треснувшая, то у нее должен существовать один целый сосед.
540D - Остров невезения (мой код: http://pastebin.com/3s6dRK3A)
Будем считать величину dp[r][s][p] — вероятность возникновения ситуации, когда в живых осталось r камней, s ножниц и p бумаг — для всех возможных значений r, s, p. Начальная вероятность равна 1, а для подсчета остальных необходимо сделать переходы.
Пусть у нас имеется r камней, s ножниц и p бумаг. Найдем для примера вероятность того, что в этой ситуации камень убьет ножницы — остальные две вероятности считаются симметрично. Количество случаев, в которых кто-нибудь умрет, равно rs + rp + sp, а количество случаев, в которых умрут ножницы, равно rs. Так как все случаи равновероятны, нужная нам вероятность равна 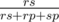 . Именно с этой вероятностью мы перейдем в состояние dp[r][s — 1][p], где ножниц станет на 1 меньше.
. Именно с этой вероятностью мы перейдем в состояние dp[r][s — 1][p], где ножниц станет на 1 меньше.
В конце, чтобы получить вероятность, что, например, камень выживет, надо просуммировать все величины dp[i][0][0] для i от 1 до r (аналогично для остальных видов).
540E - Бесконечные инверсии (мой код: http://pastebin.com/QFEMRbNP)
Запомним, на какой позиции какое число будет стоять после выполнения всех swap-ов. Теперь будем считать ответ. Ответ состоит из двух частей. Первая часть — это инверсии, образованные исключительно теми элементами, которые поучаствовали в swap-ах. Их можно посчитать одним из двух стандартных способов: mergesort-ом или с помощью сжатия координат и дерева Фенвика. Вторая часть — это инверсии, в которых один из элементов пары участвовал в swap-ах, а второй — нет. Для простоты рассмотрим тест:
2
2 6
4 8
Перестановка будет выглядеть так: [1 6 3 8 5 2 7 4 9 ...], а массив swap-нутых элементов так: [6 8 2 4].
Давайте поймем, с какими элементами будет образовывать инверсии число 8. Очевидно, такими элементами могут быть лишь те элементы, которые находятся между начальной позицией числа 8 (где сейчас число 4), и текущей его позицией. Вот этот подотрезок: [5 2 7]. Чисел на этом подотрезке, которые не участвовали в swap-ах, две штуки: 5 и 7. Число 2 учитывать не надо — ведь оно участвовало в swap-ах, и мы его посчитали на первом шаге решения.
Таким образом, надо взять количество чисел между начальной и конечной позицией числа 8 в глобальной перестановке (т.е. 8 - 4 - 1 = 3), и вычесть из него количество чисел между позициями числа 8 в массиве swap-ов (т.е. 4 - 2 - 1 = 1). Чтобы избавиться от дополнительного вычитания единицы, можно просто из правого индекса вычитать левый. Так мы получим количество инверсий, образованные элементом 8 и элементами глобальной перестановки, не участвовавших в swap-ах. Для завершения второго шага надо лишь посчитать эту величину для всех чисел, участвовавших в swap-ах. Все операции второго шага можно выполнить при помощи сортировок и бинарного поиска.









 . Все остальные случаи будут средними между этими двумя.
. Все остальные случаи будут средними между этими двумя. спортсменов в каждом списке.
спортсменов в каждом списке.
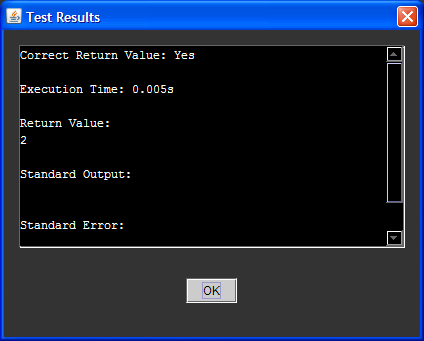
 Семплы пройдены!
Семплы пройдены! Класс с юнит-тестами
Класс с юнит-тестами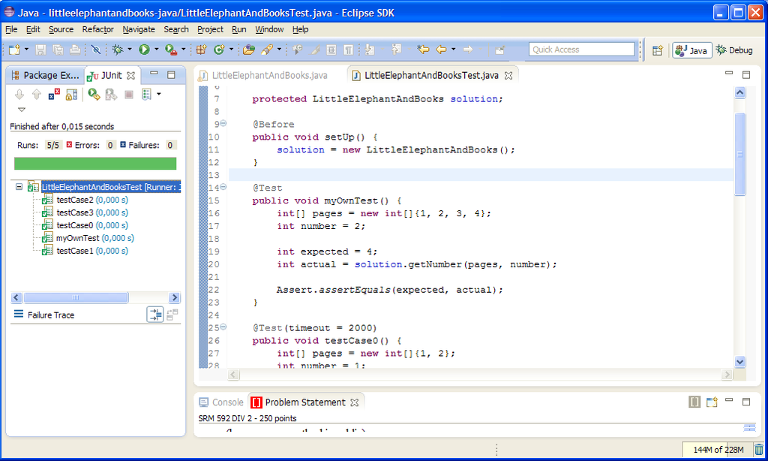
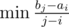 , но это за квадрат, придумай, как побыстрее. Окей, придумываю. Значит, при фиксированном
, но это за квадрат, придумай, как побыстрее. Окей, придумываю. Значит, при фиксированном 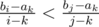 . Похоже на уравнение прямой. Давайте нарисуем в плюскости
. Похоже на уравнение прямой. Давайте нарисуем в плюскости