This is the Editorial for MemSQL start[c]up Round 2 and MemSQL start[c]up Round 2 - online version. Congratulations RAD for online round winner and Petr for onsite and overall score winner!

This editorial is written jointly by the contest's coordinators (i.e., MemSQL engineers).

335A - Banana -- AlexSkidanov

Reference solution: Jimanbanashi's 4222182

Instead of calculating the smallest possible number of sheets given a fixed n, let us instead try to compute the smallest possible value of n given a fixed number of sheets. Let k denote the number of sheets. If a particular letter appears p times in s, then it must appear at least ceil(p / k) times in the sheet. Thus we can compute the smallest possible value of n by summing ceil(p / k) over all letters. Now the original problem can be solved using binary search on k (or brute force, since the constraints were small enough).

335B - Palindrome -- AlexSkidanov

There’s a well known O(n²) solution that allows one to find a longest subsequence of a string which is a palindrome: for every pair of positions l and r, such that l ≤ r, find the length d of the longest palindrome subsequence between those positions.

d[l][r] = max(d[l][r-1], d[l + 1][r], s[l] == s[r] ? d[l + 1][r - 1] + 1 : 0).

There are two ways to solve this problem faster than O(n²) with the constraints given in the problem:

1. Use dynamic programming. For every position l and length k find the leftmost position r, such that there’s a palindrome of length k in the substring of s starting at l and ending at r. For position l and length k

r[l][k] = min(r[l + 1][k], next(r[l + 1][k - 1], s[l])),

where next(pos, s) is the next occurrence of character s after position pos. Next can be precomputed for all the positions and all the characters in advance. See DamianS's 4221965.

1. If length is less than 2600, use the well-known O(n²) dynamic programming approach. Otherwise by pigeonhole principle there’s at least one character that appears in the string at least 100 times -- find it and print it 100 times. See SteamTurbine's 4224770.

335C - More Reclamation -- AlexSkidanov

The most straightforward way to solve this problem is to use Grundy numbers. Define a segment as a maximal range of rows in which no cells have been reclaimed. Since segments have no bearing on other segments, they can be assigned Grundy numbers. There are 4 types of segments:

1. The entire river.
2. A section of river containing one of the ends.
3. A section of river blocked at both ends in the same column
4. A section of river blocked at both ends in different columns

Each time a cell is reclaimed, it splits a segment into 2 segments (one of which may have size 0). We can compute the Grundy value for all possible segments in O(r²). Then after sorting the reclaimed cells by row number, we can find all segments and compute the Grundy number for the full state.

See Dmitry_Egorov's 4221888.

Alternatively, we can compute the result directly. Suppose the game is over. We can determine who won the game just by looking at the top row and the bottom row. Let us define “parity” as the modulo 2 remainder of (r + n + c0 + c1), where c0 is the column of the reclaimed cell with the lowest row, and c1 is the column of the reclaimed cell with the highest row. Claim: when the game is over, the parity is even. This can be seen by observing that the number of empty rows is equal to the number of times the column changes. In other words, if c0==c1, there are an even number of empty rows, otherwise an odd number of empty rows. Now, given r, c0, and c1, we can determine n, and therefore the winner.

Let us consider the case where there are no reclaimed cells. If r is even, then the second city can win with a mirroring strategy. When the first city reclaims cell (a,b), the second city follows with (r+1-a,b). Similarly, if r is odd then the first city wins by a mirroring strategy, playing first in ((r+1)/2, 0), and subsequently following the strategy for even r.

Now suppose there are reclaimed cells. Let us define r0 as the number of empty rows in the segment starting from one end, and r1 as the number of empty rows starting from the other end.

Case 1: if r0==r1 and the parity is even, the state is losing. All available moves will either decrease r0, decrease r1, or make the parity odd. The other player can respond to the first two types of moves with a mirroring strategy, and the third by making the parity even again (there will always be such a move that doesn’t affect r0 or r1, based on the fact that the argument above).

Case 2: if abs(r0-r1)>=2 then the state is winning. Suppose, without loss of generality, that r0-r1>=2. Then either of the cells (r1+1, 1) and (r1+1, 2) may be reclaimed, and one of them must lead to Case 1 (since they both result in r0==r1, and one will have even parity and the other odd).

Case 3: if abs(r0-r1)<2 and the parity is odd, the state is winning. If r0==r1, then we can change the parity without affecting r0 or r1, leaving our opponent in Case 1. Otherwise, there is a unique move that leaves our opponent in Case 1.

(note that cases 2 and 3 together imply that all states with odd parity are winning)

Case 4: if abs(r0-r1)==1 and the parity is even, there is at most one move that doesn’t leave our opponent in Case 2 or Case 3. Suppose r0==r1+1. We must change either r0 or r1, since all other moves will change the parity to odd. Thus our only option is to decrease r0, since decreasing r1 would leave our opponent in Case 2. We could decrease r0 by 1, but doing so would change the parity. Thus we must decrease r0 by 2, and there is at most one move that does so and keeps the parity even. It follows that if floor(r0/2)+floor(r1/2) is even, then this is a losing position, otherwise a winning position.

See jill-jenn's extremely short 4225125.

335D - Rectangles and Square -- AlexSkidanov

Even though constraints were allowing O(k^2) solutions, in this editorial we will describe an O(n log(n)) solution. This problem has a rather long solution, involving several very different ideas: On the first step, for every rectangle we want to determine, if we were to consider this rectangle as the top left corner of a square, how long could the top and left edge of the square be (see the picture).

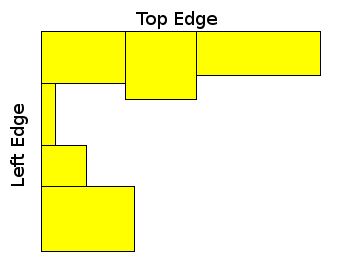
If there’s no rectangle that is adjacent to the current rectangle on the right, which has the same y1 coordinate, then the top edge length is just the width of the current rectangle. Otherwise it is the width of the current rectangle plus the max top edge computed for the rectangle adjacent on the right. Left edge length is computed likewise.

When top and left edge lengths are computed, we want to compute the max bottom and right edge length if this rectangle was the bottom right corner of the square.

On the second step, we want to find all possible square frames. Look at this picture to better understand what we mean by square frame:

To find a frame, let’s sort all the points first by x - y, and then by x (or y -- both will yield the same result). This way all the points are sorted by the diagonal they belong to, and then by the position on that diagonal. Then we will maintain a stack of pairs (position, edge length), where edge length is min(top edge length, left edge length). Position could be either x or y (within a given diagonal relative differences in xs and ys are the same). Min edge length tells us what is the largest square that could start at that position.

When we process a new point on a diagonal, first pop from the stack all the pairs such that their position + edge length is less than our position. If stack after that is empty, then the current point cannot be a bottom right corner of any square. If stack is not empty, then there could be some frames with the current point being bottom right corner.

Here we need to make a very important observation. If a square frame is contained within some other square frame, we don’t need to consider the outer square frame, since if the outer square frame is then proves to be an actual square, then the inner frame also has to be an actual square, and it is enough to only check an inner frame.

With this observation made, we can only check if the last point on the stack forms a frame with the current point, there’s no need to check any other point on the stack. Since we already know that last element on the stack reaches to the right and to the bottom further than our current position (otherwise we would have popped it from the stack), to see if we form a frame with that point it is enough to check if we can reach that far to the top and to the left. To do so, check, if position of the current point minus min(bottom edge length, right edge length) for the current point is smaller or equal than the position of the point that is at the top of the stack. If it is, we have a square frame.

When we have a frame, we move to the third step, where we check if the frame is filled in. To do that we just want to check if area within that square that is filled in by rectangles is equal to the area of the square. For every corner of every rectangle we will compute the area covered by rectangles which are fully located to the left and top from that point. To do that we can sort all the corners by x, and then by y, and process them one by one. We will maintain an interval tree where value at every position y represents area covered by rectangles processed so far that are fully above y. Then when we process a corner, we first update the interval tree if the corner is a bottom right corner, and then query the interval tree to see the area covered by rectangles to the up and left from the current corner.

Then, when we have these number precomputed, for every square frame x1, y1, x2, y2 we can just get the area for (x2, y2), add area for (x1, y1) and subtract for (x2, y1) and for (x1, y2). See the author (AlexSkidanov)'s 4234601

A possible O(k²) solution is similar, but makes checking whether or not the frame is filled much and a bunch of other checks easier. See my 4234474.

335E - Counting Skyscrapers -- pieguy

The skyscrapers in this problem depict a data structure called Skip List. Skip list is similar to AVL and red black trees in a sense that it allows O(log N) insertions, deletions and searches (including searching for lower and upper bounds), as well as moving to the next element in sorted order in constant time. Skiplist is different from any tree structures because it has a practical thread safe implementation without locks (so-called lock-free). Lock free skiplists are used as a main data structure to store data in MemSQL, and the algorithm that Bob uses to traverse the skyscrapers is an O(log N) approach, that allows one to estimate the size of the skiplist. Thus, if Bob ended up with an estimation of n, the actual skiplist size is expected to be n (so if the first line of the input file is Bob, one just needs to print the number from the second line to the output). Formal proof is rather simple, and is left to the reader. Curiously, the converse does not hold. If the skiplist size is n, the expected return value of the estimation algorithm could be bigger than n. For an n that is significantly bigger than 2^h the estimate converges to n - 1 + 2^h, but this problem included cases with smaller n as well.

Let us build up the solution one level at a time. When H is 0, the expected sum is N. Now for each additional level, we can add the expected cost of the zip lines on that level, and subtract the expected cost of the zip lines immediately below them. In the end we’ll have the total expected cost.

For some floor number H, let’s consider some left and right tower, and determine the probability that a zip line exists between them. Let L be the distance between the two towers. A potential zip line of length L and height H exists if the towers at both ends are tall enough (probability 1 / 2^H for each one), and the L - 1 towers between them are all shorter (probability 1 - 1 / 2^H for each). Thus the probability that such a zip line exists is 1 / 2^2 * H × (1 - 1 / 2^H)^L - 1.

Now, assuming that such a zip line exists, what’s the expected number of zip lines immediately below it? This is simply one more than the number of towers of height H - 1. Each of the L - 1 towers has probability 1 / (2^H - 1) of having height H-1 (given that it has height at most H-1) -- use conditional probability (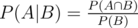) to calculate this. Thus the expected number of zip lines immediately below a zip line of length L and height H is 1 + (L - 1) / (2^H - 1).

For each length L, there are N - L possible zip lines with this length on each level. We multiply probability by cost for all possible zip lines to attain the expected value.

The final answer is therefore

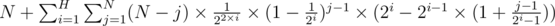
It turns out the inner loop can be computed using matrix multiplication, for a running time of O(H log N). -- although the constraints is low enough that using matrix multiplication is an overkill -- O(H * N) will do.

See the author (pieguy)'s 4234465. ...apparently this solution is much shorter than the "easier" problem's :)

Congratulations Petr and tourist for the only persons solving this problem in-contest both on-site and off-site!

335F - Buy One, Get One Free -- pieguy

This problem is equivalent to maximizing the total value of items that we can get for free.

First, process the items into <#value, #number_of_items_with_that_value> tuples, which means we have #number_of_items_with_that_value items of value #value. Then, sort the tuples in descending order of #value.

Iterate over those tuples and let #pieguy be an empty multi set()

For each tuple <#val, #num>, we can calculate #max_free, the maximum number of items (not value) that we can get for free up to this point easily.

So, we want to populate #pieguy so that it contains exactly #max_free “things”. #pieguy is special, in that we can compute the maximum price that we can get for free for n items by summing up the n most expensive items in #pieguy. How could #pieguy do that?

For now, you may assume that each element of #pieguy contains the value of a single item that can be gotten for free. Thus, summing n items = value of n items that can be gotten for free. This is not correct, of course, since not all n arbitrary items can be simultaneously gotten for free in tandem, but we’ll come back to it later.

We’re now at <#val, #num>, and we have #pieguy from previous iteration. #pieguy contains the previous #max_free elements. Assume that #num <= number of items more expensive than this value, for otherwise the remainder are ‘dead’ and useless for our current purpose. In particular, for the first tuple we process, we assume that #num is 0, since all of them cannot be gotten for free.

Suppose we want to obtain exactly #max_free items. How many of the #num must we use?

Let’s arrange the current members of #pieguy in descending order. For example, if #pieguy has 5 members:

A B C D E

Let’s arrange #num #val under #pieguy so that the rightmost one is located on position #max_free. For example, if #num is 6 and #max_free is 8 and #val is V....

A B C D E
    V V V V V V

These 6 Vs will be competing for a spot in #pieguy.

Now...

1) what happens if C < V? This means, instead of making C free, we can make V free instead! (if you’re wondering why this is possible, remember that #pieguy definition I gave you was not entirely honest yet). So, we replace C, D and E with all Vs, and we get our new #pieguy! A B V V V V V V (this should be sorted again, but C++’s multiset does that automagically).

2) otherwise, C > V. So, V cannot contend for the 3-th place in #pieguy, it has to contend for a place larger than or equal to the 4-th.

Now the fun begins! If you want to contend for the 4-th place, any solution MUST HAVE AT LEAST 2 V s (remember that the 4-th place is used in a solution consisting of at least 4 free items). In general, if you want to contend for the #max_free — i -th place, you MUST HAVE AT LEAST #num — i Vs. #proof? is easy, exercise (i’m honest!)

Okay, so back to contending for the 4-th place. If D is still > V, we proceed. Otherwise, we know that D < V. This means, E and any element after E is also < V! Thus, we can replace all elements after or equal to E with V! The problem would be the final element of #pieguy.

When the final element of #pieguy is included in the sum, it is only included in the sum of all n elements of #pieguy. You do this when you want to calculate the maximum sum of values of free items you can get when getting exactly #max_free items. Any such solution must include all #num elements with value #val. We have included #num-2 Vs in #pieguy. Thus, the final element of #pieguy must somehow contains 2 Vs! So, elements of #pieguy actually can do this. Instead of containing a single elmeent, each element of #pieguy is more of an “operation” that adds several value and removes several value. In our case, we want to add 2 Vs and remove something. The something? The smallest element that we can remove (the ones that we haven't removed)! C! (if you're wondering why not D or E, it's because (again) #pieguy is special -- it only forms a solution if the most expensive t are summed, not if some are skipped. -- we cannot skip C if we want to use D).

So, Insert 2V — C into #pieguy, and the rest, insert V into #pieguy. 2V — C is < V, so summing all elements of #pieguy correctly found out the max value when we receive #max_free free items!

Right! Cool! ...except that 2V — C can be negative. Why would we want to insert negative stuffs into #pieguy? We don’t! Actually, we check if 2V — C is negative. If it is, we continue instead, and check 3V — C — D and so on, under the same reason.

That’s it folks! I skipped some details of why this works (for example, that the number of V selected is always sufficient to guarantee solution in #pieguy), but they're easier to see once you get this large idea. The result is then #pieguy.last_element

See pieguy's beautiful 4234458.

UPD: Editorial

Hello!

After the barrage of non-standard contests (memSQL, ABBYY, Yandex), we present you a standard and fun (and strange) Codeforces round! This contest is prepared by Indonesian coders: fushar, jonathanirvings, and me (dolphinigle)! fushar wrote D2-E/D1-C, jonathanirvings wrote D2-B, and I wrote the rest. For me, this is my fourth contest, after Codeforces Beta Round 87 (Div. 1 Only), Croc Champ 2012 - Final, and last week’s MemSQL start[c]up Round 1 (only 1 problem there though). We would also like to thank Gerald for helping with the contest preparation, Delinur for translation, and MikeMirzayanov for the system!

I think this contest is stranger than usual -- The statements are strange, there are pictures everywhere, etc. There is a single problem with very lengthy statement (I am unable to shorten it further without losing clarity, I'm sorry), but I think it's very clear. The other problems have relatively short statements.

fushar drops a message for you:

We think that the solutions to all problems are satisfying to discover. We want to add a special note: you might find that the solutions will not be too “usual” :).

Happy solving!

UPD: The contest is finished! Editorial will be posted tomorrow by fushar. Hope you enjoyed the contest!

...Div1-D 329D - The Evil Temple and the Moving Rocks was a little too strange I guess.

UPD: Congratulations to the winners!

D1:

1. espr1t

2. RAVEman

3. Psyho

4. Petr

5. Shik

D2:

1. RNS_MHB

2. Parsa.pordel

3. s0en1it

4. RaJin

5. darrenhp

You guys are certainly good at ad hoc problems! :)

UPD: Komaki, followed by Marcin_smu finally solved the last problem 329E - Evil after the contest. During the contest, they submitted some solutions with the right idea but got caught by pretest. You guys are awesome!

Croc Champ 2012 - Final

Final Update: Congratulations to the prize winners!

• First place: neex.emil — 100000 rubles
• Runner Up: Dmitry_Egorov — Apple MacBook Pro 15
• 2nd Runner Up: vepifanov — Apple MacBook Pro 13

Videos for the onsite round (posted by ivan.popelyshev): 1 2 3 4 5 6

Congratulations to the winners of the mixed group (onsite & offsite)!
ivan.metelsky
YuukaKazami
neex.emil

rng_58 deserves honorable mention for the only competitor to correctly submit both D and E :)

Editorial.

Hello Codeforces!

I am glad to welcome you — both onsite and out-of-competition competitors — to the final round of Open Moscow Programming Championship By CROC. I am the writer of this round — Gerald, ivan.popelyshev and Delinur helped me in the preparation of the problems. This is my second round in Codeforces, so far, thanks to the Codeforces team and MikeMirzayanov for giving me this opportunity again!

Please note that this round is held in conjunction with its onsite counterpart, so its starting time may be delayed. Also, since MikeMirzayanov is very busy with the onsite contest at the moment to decrease the load (to avoid any disaster for the onsite competition), I apologize that you may not receive any email reminder about this match.

I've taken feedbacks from my last match into account, so the pretests will be fairly strong. The match should be more interesting for you if you decide to try and solve as many problem as possible, instead of stopping and hacking other codes early in the match :)

The rules below are copied-modified from Ripatti's post:

Competition will happen by usual rules of Codeforces, with hacks and score falling in process of time. The three championship winners will be awarded valuable prizes:

• 100000 rubles for the first place
• Apple MacBook Pro 15 for the second place
• Apple MacBook Pro 13 for the third place

Please remember that the round will be rated only for onsite participants and Division 1 contestants, since the problemset may be more tricky than usual (or it may not be :) ). Division 2 coders can participate, but it will not be rated for them.

There will be five problems ordered by approximately increasing complexity. The scores will be 500-1000-1500-2000-2500. Don’t forget that during contest your solutions will be tested on a small set of pretests. Testing on full testset will be after end of the round. Pretests can don’t cover all cases of input data, so you should test your solutions very carefully.

It is strictly forbidden to publish statements/solutions of the problems before round will be end. Also you shouldn’t to talk about problems, discuss some things about possible solutions of them. Let’s be honest! You can discuss problems after the end of round.

Good luck everyone! I will be watching :)

This is the editorial for Croc Champ 2012 - Final

Remarks

One day, I applied to write another round in Codeforces. To my surprise, I was offered to write CROC instead. I'm quite surprised they offer me (an unknown programmer from a notorious country) to write for such an important match! So I happily oblige — kudos for the open culture nurtured by Codeforces!

I like most the problems of this final round. I think all of them are beautiful in some aspects :). Oh, and all of them emits such concise solutions ;).

Problem A

Author: dolphinigle
Ad Hoc I supppose...

This problem is equivalent to calculating the number of reachable locations from point (0, 0) by doing the allowed moves.

The naive solution is to process the information one by one from first to last, and to keep track on all the reachable positions.

Claim: At any moment in time, all reachable locations as described above forms a "diamond".

An extremely informal proof is by induction:

For instance, let's use the first example:

UR UL ULDR

Initially, there's only one possible location (namely, (0, 0)). It forms the basis of our induction: a diamond with width=1 and height=1.

"UR" (and also "DL") extends the width of the diamond into a 2x1 diamond:

Then, "UL" (and also "DR") extends the height of the diamond into a 2x2 diamond:

Finally, "ULDR" extends both the height and the width of the diamond into a 3x3 diamond:

And so there's 9 possible locations.

To see that this claim is true, suppose by induction our locations so far forms a diamond. By symmetry we only need to see that in the "UR" case, its width is increased by one (I'll omit the similarly seen "ULDR" case). The idea is the new possible locations = the previous diamond shifted one step up UNION that diamond shifted one step right. Indeed, the union of these two diamonds accounts for both the "U" and the "R" moves.

It's not hard to proof that the union of two diamonds with equal dimension that is displaced by vector (1, 1) forms the same diamond with its width increased by 1.

So, the solution is to keep track the dimension of the diamond, starting from a 1x1 diamond. Then, simply return width * height.

Reference: See 1631223 by Endagorion (my favorite CF author! :) ).

Problem B

Author: dolphinigle
Geometry

Since there are at least one flamingo, all binoculars will be able to see at least one flamingo. When a binocular is able to see more than one flamingos, then those two flamingos and the binocular must form a line. How many such lines are there?

Instead of iterating for each pair of binocular and flamingo, we iterate over each pair of flamingos. These two pair of flamingos completely determine the line as described above. If there does not exists a binocular in this line, we can ignore this pair and continue. Otherwise, calculate the number of flamingos in this line, and let it be one of the possible number of flamingos visible from that binocular.

After this is done, simply sum the maximum number of flamingos of each binocular. This works in O(M^3). Note that this problem can be made to run in O(M^2 log M), but coding that solution is sort of... boring ;3.

For instance, see vepifanov's 1631294

Remarks

Actually havaliza prepared a much nicer B problem. Unfortunately, we found out at the last moments that the problem may be too similar to a problem (that is used a looooooooong time ago), so we decided to switch that problem with something else. And that's why this problem is here.

It's too bad, the problem proposed by havaliza is actually very nice. Perhaps we will see it in one of the upcoming rounds :)

Problem C

Author: dolphinigle
DFS

Let's drop the (modulo K). That is, the rule becomes:

• X->Y implies that Y = X+1
• Y->X implies that Y = X-1

While we still dropping the "modulo K" thingy, we try to calculate the values of each node. We iterate over each node, and if we haven't processed the node:

• Number the node 0 (or any other number you like). let's denote this by no[i] = 0.
• DFS the node:
  • DFS(X): if there exists X->Y, then no[Y] = no[X]+1. This follows from the first rule.
  • DFS(X): if there exists Y->X, then no[Y] = no[X]-1. This follows from the second rule.
  • If Y is renumbered (that is, the algorithm has renumber it in the past and we renumber it again), consider the difference between the two numbers. We claim that this difference, if not zero, must be a multiple of K. To see this, suppose the two numbers are A and B. By the way our algorithm works, that node must be able to be numbered A or B. Hence, A == B (mod K) must holds. But then, A-B == 0 (mod K) implies that (A-B) is a multiple of K.
• If a non-empty multiple of K (let's say it's CYCLEN) is not found in the step above, we claim that the answer is the maximum possible answer: N. Indeed if no such value is found, it means that renumbering the nodes into no[i] % N be correct, since every edge is already consistent with no[i].
• Otherwise, we can simply brute force all divisors of CYCLEN and try each of them. Since "trying" uses O(E) time (that is, by setting each number into no[i] % K and checking whether the two rules holds for all edges) , we have a O(number_of_divisors * E) algorithm, which with the given constraints is less than O(E * sqrt(N)).

For instance, sexyprincess91 implemented this. 1632321

Problem D

Author: dolphinigle
Dynamic Programming, Probabilities, and a little Greedy

Suppose we have decided to bring N1 T-shirts of size 1, N2 T-shirts of size 2, ... NM T-shirts of size M. By the linearity of expectation, the expected number of engineers that will receive a T-shirt is equal to the sum of the expected number of engineers that will receive a T-shirt of size K, for all K.

Suppose we bring Ni T-shirts of size i. Define a random variable Xij as the number of engineer that will receive the j-th T-shirt of size Ni that we bring. Hence, the expected number of engineers that will receive the Ni T-shirts of size i that we bring is equal to the sum of Xij over all j. Since Xij is either 0 or 1, Xij is equal to Pij, the probability that there will be an engineer that will receive the j-th T-shirt of size i that we bring. This is equal to the probability that there will be at least j engineers that fits inside T-shirt of size i.

As a result of our discussion, to maximize the expectation, it boils to maximizing the sum over Xij. Hence, we receive our first solution: Calculate the value of all Xij, and pick the N largest value. A DP implementation allows us to accumulate all Xij value in O(N*N*M) time, yielding an O(N*N*M) solution.

We will now reduce the time limit to O(N*N + N*M). Notice that the algorithm above only need us to find the N largest values of Xij. Denote by f(n, i, j) the probability that, amongst engineers numbere 1 through n, at least j of them fits inside T-shirt of size i. f(n, i, j) can be computed with the following recurrence: f(n, i, j) = f(n-1, i, j-1) * fit_chance(n, i) + f(n-1, i, j) * (1.0 — fit_change(n, i)) Where fit_chance(t-shirt, engineer) is the probability that engineer fits inside the t-shirt size.

The formula above can be inferred from simple logic: if the n-th engineer fits inside t-shirt of size i (with fit_change(n, i) probability), then f(n, i, j) is obviously equal to f(n-1, i, j-1). Otherwise, it'll equal f(n-1, i, j).

Now, observe that Xij = f(N, i, j). Indeed, this is one of the possible DPs that can lead to the O(N*N*M) solution. However, we will show that we do not need to compute f(n, i, j) for all possible inputs if we're asked to find only the N largest values of Xij.

The key observation is the following obvious fact. If Xij is included in the N largest values, then Xi(j-1) must also be included there. Inductively, Xik for k < j must also be included in the N largest values. Indeed, it's obvious that Xij must be non-increasing with respect to j.

Hence the algorithm works as follows. First, we create a pool of numbers Xi1, for all i, totalling M numbers. Then, we iterate N times. In each iteration, we pick the largest number in the pool, say, Xij. Then, we add Xij as one of the K largest values. Then, we take out Xij from the pool, and insert Xi(j+1) as its replacement. That it correctly picks the N largest Xij values follows immediately from our argument in the paragraph preceeding this.

Now, if we use the recurrence f(n, i, j) above to compute each Xij, what is the complexity of this algorithm? If we memoize f(n, i, j), we claim that it's O(N*N + N*M). To see this, we notice that the only values required to compute f(n, i, j) using the recurrence above are the values f(m, i, l) such that m <= n and l <= j. However, we notice that due to how our algorithm works, when we need to compute Xij, we must have already computed Xi(j-1) before, so that all values f(m, i, l) for m <= n and l <= j-1 are already available. So the only NEW values that we need to compute are f(m, i, j), m <= n. There are n such values.

Since we need to compute at most O(N) values of Xij, the total complexity this part contributes is O(N*N). Depending on how you implement the "pick largest from pool" algorithm, the total complexity can be either O(N*N + N*M) or O(N*N + N*log M).

Yes, somebody did this in the contest :). Dmitry_Egorov 1632270 saved my problem from loneliness :)

Bonus Section: Now here's an extremely interesting solution shown by the following Python pseudocode:

values = []
for size in range(M):
  i = 1
  while (val = f(N, size, i)) > epsilon:
    values.append(val)
    ++i
  end
end
Print the sum of the largest N values in array values.

Its correctness is immediate as long as epsilon is reasonably small (since f(N, size, i) is non-increasing with respect to i). What is the complexity of this very simple algorithm?

I am unable to come up with a hard, solid proof, but since f(N, size, i) exponentially falls (except if some probabilities are 1, in which case some other T-shirt must have less value to worry on), the complexity is somewhere near O(N * N). Indeed for the current set of test cases, its speed exceeds that of the intended solution.

Although rng_58 do not implement this exact algorithm, he used the <EPS ignore idea in his solution 1631960

Remarks

I really really wanted to link Gerald's handle in the statement :). Too bad Codeforces doesn't support it.

Problem E

Author: dolphinigle
Very greedy

Brute force P: the number of Packages each kid will have at the end. There are at most N/M possible such value. We will assume that P is fixed during our discussion.

If we know P, we know that if kid i purchases a total of X candies, then kid i+1 must purchase at least X+P candies (1 more than each package purchased by kid i). Hence, assume that money[i] <= money[i+1] — P.

Two consecutive packages purchased by the SAME kid must differ by at least M. Indeed, otherwise there are less than M-1 packages for the other M-1 kids to buy from (Pigeonhole rocks by the way).

For the sake of our discussions below, we refer to the following example with N=8, and M=3 kids. The allowances of the kids are 7, 10, and 14.

Suppose we know all candies kid 0 purchased (red bags denote the packages kid 0 purchased).

We claim that the optimal solution can be computed rather... easily with the following greedy algorithm: (assume that the candy packages kid 0 purchase is sorted in an ascending order). We iterate over the remaining kids, starting from kid 1. First, let the kid purchase the minimum possible candies:

Next, if the allowance is still greater than the sum of candies, and if one of his package(s) can still be shifted to the right while maintaining the condition that a possible solution exists, do so. If there are multiple package(s) that can be shifted, shifting any of them does not change the optimal answer.

Note: since we've assumed that money[i] <= money[i+1]-P, the only condition is that between the package purchased by kid 1 an the next package purchased by kid 0, there exists at least N-2 packages. For instance, this is illegal, since there is no package that kid 2 will be able to purchase between 4 and 5.

We iterate this once more for kid 2, obtaining:

And we're done. It's arguably the maximum possible value, since there is no reason why we shouldn't shift a package for a kid to the right if we can (formal proof by contradiction).

Claim: If we know the packages for kid 0, the maximum total candies purchased can be computed in O(M), where M is the number of kids.

The algorithm simulates our discussion above. However it is not obvious how to do that in O(M). So, suppose kid 0 purchase the candies like this:

Now, try putting the other P-1 packages into the minimum possible locations:

The packages inside the yellow boxes denote what we will call FREEDOM. Basically FREEDOM is the count on how many times we can at most shift a package to the right as in our discussion above.

Now, consider kid 1. First, as in our discussion, kid 1 takes the minimum amount of packages, which is equal to sum[kid 0] + P. Next, he will attempt to shift the packages if possible. Notice that the only thing that affects the overall sum of the candy is only the number of shifts performed, not which package actually got shifted. So, this means that, the amount of shift can be easily calculated by min(money[1] — (sum[kid 0] + P), FREEDOM). And then, FREEDOM is deducted from this value, while the amount of candies purchased by kid 1 is incremented by this value.

Hence, simulating the algorithm in our discussion if we're only to output the total amount of candies can be done in O(M).

The result of our discussion so far is this. Notice that the last algorithm only depends on how many candies kid 0 purchased, and FREEDOM.

Now we will remove the assumption that we know which packages kid 0 decides to purchase.

Claim: It is optimal for kid 0 to purchase as many candies as possible.

Suppose kid 0 does not purchase the maximum possible of candies he can purchase. Now, consider whether or not kid 1 "shifted" his candies.

• If he shifted any of them, say package X, then instead of purchasing package X-1, kid 0 should purchase package X, improving the overall amount of candies. That is, instead of
  
  It's better to
  
• If kid 1 did not "shift" his candies because the amount of money he spent is already equal to his allowance, then the amount of candies purchased by kid 0 must be maximum since money[i] <= money[i+1] — P.
• Otherwise, we can apply this inductively to kid 2 and so forth. That is, instead of
  
  It's better to
  

Okay, now we know the sum of candies that we should give to kid 1. Since the performance of our algorithm increase with FREEDOM, we should next try to maximize FREEDOM.

Claim: FREEDOM depends only on the position of the FIRST candy package purchased by kid 0.

This can be shown by simple computation, and its equal to N — pos — M*P (or something like that).

Hence, we should try to minimize the first candy package purchased by kid 0, while keeping the sum maximum. This can be done in O(1) using a bunch of N*(N+1)/M * P formulas.

Hence, since there are N/M package numbers to be brute forced, and each iteration uses O(M) time, the total complexity is O(N/M) * O(M) = O(N).

For instance, see 1632210 by rng_58 (again :) ).

Epilogue

Thank you for participating in the match!

Hope to see you again!

Time Capsule Remarks (planted before the contest)

Due to popular demand, today's problem statements are made to be as short as possible without too many (but existing!) embellishment. All of them are thinking-based problems (i.e., implementation is the easier of the two) - so I'm generally happy with the problems :). I hope nobody found them to be too easy :S

As you may have noticed, we decided not to give devastatingly weak pretests. I guess it's just really evil to give weak pretests for my first match.

And so, the editorial begins...

Remarks

I'm sorry - but I don't have access to my usual graphic editing tool and so, the graphics are fairly limited :) (Example: Lawnmower's pictures must be the ugliest lawnmower I have ever seen! (Is it even a lawnmower?) Not to mention I don't look like the actor at all...)

D2-A: Tram

If we know the number of people inside the tram at all possible time, then the answer is the maximum of such. We observe that the number of people inside the tram changes only at tram stops. The conclusion is that the answer will be the maximum of the number of people inside the tram directly before arriving at a particular stop and directly after leaving a particular stop (the more observant readers can notice that using only one of these is sufficient).

It's sufficiently easy to calculate the number of people inside the tram directly before and after leaving a tram stop.

D2-B: N Little Pigs

No... not maximum matching ;)

So, an equivalent less-evil rewording of the problem would be: "Return the number of wolves that are adjacent to at least one pig".

To see this, since each pig has at most one wolf adjacent to it (the constraints impose that) we don't need to worry at a single pig may get eaten by two different wolves. Hence, each wolf can eat any of the pig adjacent to it.

Remarks

It's more interesting to reverse this problem isn't it:

Each pig will be adjacent to at most one wolf

becomes

Each wolf will be adjacent to at most one pig

Can you solve this one? (Of course, not using network flow mind you ;) - that's overkill)

D2-C / D1-A Party

We let an employee without a manager called as root. There's an edge from a manager to an employee that he/she manages.

First notice that the graph is a collection of directed trees. Hence, we can assign a depth label to each node - denoting the number of nodes on the simple path from the root to it. The answer is then the maximum depth a node has.

Why?

First, the answer is bounded below by this number because any pair of employees in this path cannot be in the same group. Second, since the graph is a tree, each node in the graph has a unique depth label assigned to it. Simply put all nodes with the same depth in the same group. It's fairly easy to see that no one will be the superior of another within a group, for otherwise their depths will not be equal.

Remark

You might notice that there exist an O(N) implementation of the above algorithm, yet the constraint is 2000. Well, this problem was swapped with the D1-B because the previous D1-A was thought to be harder than expected. And so, in the process, we also decrease the constraint for N from 200,000 to 2,000. I hope you like it :)

D2-D / D1-B: Lawnmower

First, let's observe a particular strategy that turns out to be optimal at the end of our discussion.

Suppose we're on a row, facing right. This strategy say that we need to move to the right as long as there is a weed to the right of us either on this row or on the row directly below us.

The idea is that we need to mow that weed, hence, we need to move there. If it's in the same row as us, it's fairly obvious we have to mow that before going down. If it's at the row directly below us, since we can't move to the right in the row below us (since we'll be facing left there) we need to move there before going down.

The strategy then says that if we no longer need to move right, we go down, and face left. Repeat this until all weeds are mowed (replacing left and right in the discussion above) - and we have our strategy.

This strategy is optimal. Proof is using induction - but it's not particularly interesting, so the idea is given instead.

Suppose we're on a row, facing right, again. If there exist a weed to the right in this row or below us, then any solution will necessarily move right as far as our strategy goes (for the reason we discussed above). Some solution however choose to go further right despite having no weed in this row or the row directly below us. This solution is not optimal if we need to go left directly after going down, for we can just simply go down instead of going right-down-left. On the other case, if we don't need to go left directly after going down, then it means that we go down twice-in-a-row! Hence, instead of moving right in this row, we go down twice, then move right there. And then the induction can continue and the proof can follow.

Remarks

I guess the actor should be Toastman instead :).

Anyway, so sorry to disappoint you, but we decided to add some pretty strong pretest to this problem, despite the fact that many solutions will probably forget to take care of two consecutive empty rows. But still, the pretest we gave only consist of one column, so feel free to hack the stragglers :) (not that this suggestion matters after the contest but still...)

D2-E / D1-C Plumber

To solve this problem, let's imagine that the left and top sides of the grid also determines whether the pipe adjacent to that side has an end connecting it to the side or not. There are 2^(N+M) ways to pick them. We claim that if we fix them (i.e., pick one of the possible 2^(N+M) ways, then the entire grid's pipes are fixed).

To see this, notice that each pipe segment will have either one vertical end (it either have end on the top or end on the bottom) and one horizontal end (left or right). We can pick any 4 combinations of them. Suppose we pick a row, and determine whether the leftmost pipe should have an end to the left of it, or not. Suppose it doesn't have an opening to the left. It means that the leftmost pipe should have an opening to the right, the next pipe should have an opening to the left, the next pipe to the right, and so on. Continuing this way, we have fixed the horizontal ends for an entire row - and only that. Hence, if we pick one of the possible 2^(N+M) ways to pick the ends, then the horizontal ends of each row and vertical ends of each column is fixed. Since there is exactly one pipe segment that has a particular configuration of ends, there is exactly one possible completed grid for each of the 2^(N+M) ways to pick the ends.

Hence, the solution works by first checking if a solution exists. Any pre-assigned pipe simply sets whether or not its corresponding row and column has an end at the left and top side. We need to check that no two pipes sets this value contradictorily. If any of them are contradictory, then we return the answer as 0. Otherwise, we return 2^(number of rows without preassigned cell + number of columns without preassigned cell).

D1-D Unambiguous Arithmetic Expression

This problem is solved using Dynamic Programming. The somewhat straightforward dynamic programming is to represent the state as {start_pos, end_pos}, which represents the number of unambiguous arithmetic expression on the substring of the input starting at start_pos and ending at end_pos. This however has a complexity of O(N^3) and is not suitable for our problem.

The solution uses the state {pos, braces}. This state is somewhat tricky to explain. This means that we have read the first pos characters in the input. We're expected to read a single unambiguous arithmetic expression, close it with some number of brackets that we don't care (to be explained below), and then, if braces is zero, that's it. Otherwise, we're then expected to read a binary operator (either + - * or /), then open a bracket, then move the state to {pos + some_value, braces-1}. That is, braces keeps track on the number of second operands of binary expression that we need to make.

For an example how this works, let's try to solve a particular test case:

"++0*+1"

Let's denote with quotes the part of the input that we haven't processed. We're going to create the unambiguous arithmetic expression by scanning it left to right and making some choices.

There are three choices:

1) Create a unary expression. In the example above,

"++0*+1" -> +("+0*+1"

We don't really care about where the closing bracket is yet.

2) Create a binary expression. In the example above,

+("+0*+1" -> +(("+0*+1"

How does this tells that we will need to create a binary expression? The second open bracket does not have any operator preceeding it. The only thing that can makes this a proper prefix of an unambiguous arithmetic expression is that if this bracket belongs to the first operand of a binary expression.

For our example, we suppose we read another unary expression

+(("+0*+1" -> +((+("0*+1"

3a) Read an integer. In our example above,

+((+("0*+1" -> +((+(0))*("+1"

There are two questions. a) how do we know the number of closing brackets we have to make? This is actually easy - for every open bracket we have, if it's for a unary expression, we simply close and repeat. Otherwise it's a closing bracket for possibly the first operand to a binary expression, so we close it, and we read a binary operator (* in the example above), and try to read the second operand of the binary expression.

Finally:

+((+(0))*("+1" -> +((+(0))*(+("1"

3b) We try to read an integer again and we have no open brackets that belongs to the first operand of a binary expression, and we have ourself a possible answer.

+((+(0))*(+("1" -> +((+(0))*(+(1)))

So, in the state {pos, braces}, pos determines the starting location of the remaining unprocessed input. braces indicates the number of open brackets that belongs to a binary expression. So, in the examples above:

1)

"++0*+1" -> +("+0*+1" is represented by

{0, 0} -> {1, 0}

More specifically, for unary expressions, {pos, braces} -> {pos+1, braces}

2)

+("+0*+1" -> +(("+0*+1" is represented by

{1, 0} -> {1, 1}

More specifically, for binary expressions, {pos, braces} -> {pos, braces+1}

3a)

+((+("0*+1" -> +((+(0))*("+1"

{5, 0} -> Done

More specifically, {pos, braces} -> done if braces is zero and the remaining input forms a single integer.

Remarks

My favorite problem of this match (because it's hard-to-think and easy-to-code) ;). This turns out to be the hardest problem of the match.

During the match, three coders (shik, ivan.popelyshev, and watashi) submitted solutions which I think works in N^2. Petr submitted a solution that (I think) uses Catalan number, while Egor submitted a solution which uses polynomial to quickly count each of the dp values (see his comment in the Editorial). tourist submitted a solution which uses a highly-optimized inner loop with no branching and expensive operations (only a single multiplication) - he cleverly avoid branching in his code.

D1-E Races

We process the roads one by one. Associated with each road is the races whose UBi is that road (i.e., races that 'ends' at that road). We will discuss the Dynamic Programming solution first, then improve it with a data structure into the optimal solution.

Let's say we're going to process a road. Our state is this : DP[X] is the maximum possible profit such that the last X roads before this road are fixed and the X+1-th road before this road is NOT fixed. We are going to compute the value of DP for the next iteration, let's call this FUTURE. FUTURE[0] is obtained if we don't fix this road, FUTURE[0] = maximum amongst the value of DP. Otherwise, if we decide to fix this road, then for each of DP[X], FUTURE[X+1] >?= DP[X] - cost to fix the road + all races' profit that ends at this road and whose starting point is not before X roads from current road (i.e., all the races that is contained and ends at this road). This should work in N^2 + N * M. It can be improved to N^2 + M

The data structure approach is slightly different. We will use a segment tree that allows finding a maximum value in a subset and modifying the values of a range, all of which should work in either O(1) or O(log N). The segment tree will consist of N+1 leaves. However, not all the leaves are active at the start of the algorithm. At the start, only one leaf is active and it corresponds to the initial value of DP[0]. Next, we can compute the maximum value amongst all active leaves in O(log N). Then, we create a new active leaf that corresponds to FUTURE[0]. This will be located in the same tree however, the values represented by the leaves will be shifted one to the right - this is done implicitly (for example, we use the last node as DP[0] for the first iteration, but treat it as DP[1] for the next, and so on). These shifted values will correspond to FUTURE[X], since we notice that FUTURE[X] = DP[X-1] - cost to fix the road + races that this series contains and ends at this current road (i.e., it's value directly depends on the leaf BEFORE it was shifted). Next, we decrement the value of all these new leaves (except FUTURE[0]) by the cost to fix the road (in O(log N)). Finally, for each race that ends at this road, we increment the value of the leaves that contains this race. This will be continuous, i.e., FUTURE[X] for X in [race_len, INFINITY]. This can also be done in O(log N). Since a race ends at at most one road, the total complexity this will contribute is M log N.

The answer will then simply the maximum value amongst all members of the tree.

Remarks

This is one of the problems I submitted to this year's IOI but didn't got accepted - I sort of agree that this doesn't suit IOI very well. IOI likes a non-numeric output :) #goparrots!