In the light of the current Russian internet laws obscurantism, an insistent wish to move the site abroad emerged.
Let's try to choose the name you would like most of all:
https://polldaddy.com/poll/7857563/
(I have a weak imagination, so don't bother to suggest your options — you can check them, for instance, here)
UPD Thanks everybody, the poll finished. Results: the winner is e-maxx.io (25%), and the second by popularity is e-maxx.us (16%).









 Hello, CodeForceans!
Hello, CodeForceans! -solution is somewhat easier, - it is based on binary search (for building palindromic array and for answering the queries) and, for example, hashes (for comparison of two substrings).
-solution is somewhat easier, - it is based on binary search (for building palindromic array and for answering the queries) and, for example, hashes (for comparison of two substrings).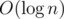 , so the total solution is
, so the total solution is 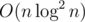 . Alternatively we can use sparse-table to reach
. Alternatively we can use sparse-table to reach 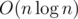 asymptotics (sparse-table is a table where for each position
asymptotics (sparse-table is a table where for each position 
