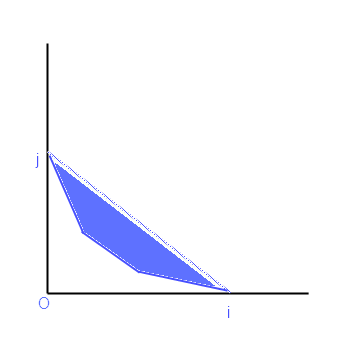
The most important step on the way to solve this problem - is to understand that it's enough to consider only such rotations of the polygon, that one of its sides lies on the side of the room.

Let's try to understand this fact. Suppose that the fact is wrong, and there exists such a position of vacuum cleaner, that neither of its sides lies on the side of the room. Denote as i and j the numbers of vertices that lie on the room sides. It's easy to understand that the polygon form between vertices i and j doesn't make any sense itself: for each rotation we can see that from the area of triangle OP[i]P[j] some constant area is subtracted, while the concrete value of this constant depends on the polygon form.

That's why we see that the polygon form doesn't influence on anything (if we have fixed numbers i and j), and we have just to minimize the area of right-angled triangle OP[i]P[j]. But, taking into account that its hypotenuse is a constant, it's easy to see that the minimum is reached in borderline cases: i.e. when one of the polygon sides lies on the room side.

So, we've proved the fact. Then we have to invent fast enough solution. We have already obtained an O(n²) solution: iterate over all sides of the polygon (i.e. iterating over all possible i), mentally push it to one side of the room, then find the threshold point j, then calculate answer for given i and j. Let's learn how to do these both things in O(1).

In order to do the first thing (finding j) we can use a method of moving pointer: if we iterate over i in the same order as in the input file, then we can just maintain the right value of j (i.e. when we move from i to i + 1 we have to increase j several times, while it is getting further and further).

In order to do the second thing (the area calculation) we have to do some precalculation. For example, we can find the mass center Q of the vacuum cleaner, and pre-calculate all partial sums S[i] - sums of all triangles QP[j - 1]P[j] for all j ≤ i. After this precalculation we can get the answer for every i and j in O(1) as a combination of difference of two values from S[] and two triangles' areas: QP[i]P[j] and OP[i]P[j].