Hello $$$\mathfrak{Code}\color{blue}{\mathfrak{Forces}}$$$,
This blog assumes that you are already familiar with the basic concepts of Graph Theory.
First of all I'd like to thank my coach fegla who taught me those tricks and I'll try to share some of them with you. I think that there is no tutorial for this graph representation (at least no English tutorial, I've seen some Chinese coders using this representation). So, here we go!
I'd like to introduce this uncommon graph representation (I'm not sure if it has a proper name or not, but we used to call it adjacency edge list).
Let's say we have this directed graph: note that the numbers on edges are just the order of adding edges:
0 1
0 3
1 2
2 3
0 2
2 4
3 4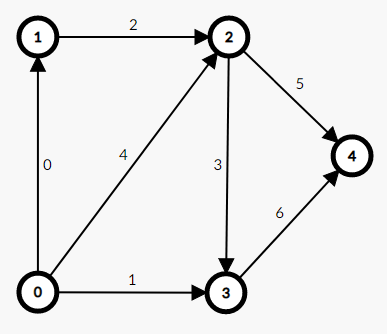
We will represent this graph using only two arrays/vectors:
int head[MAX_NODES]; the size of this array will be the maximum number of nodes, and the value for each node will represent the index of the latest added outgoing edge in the edges array.
edgeData edges[MAX_EDGES]; the size of this array will be the maximum number of edges, it contains all the needed data from the edge. and the edgeData must contain nxt which will point to the index of the next edge.
Let's see all the outgoing edges from node $$$0$$$, the indices of the edges in order are $$$[0, 1, 4]$$$. initially head[0] = -1 which means that there is no outgoing edges from node $$$0$$$.
Let's add the edge with index $$$0$$$ 0 1 we will update edges[0].to = 1, edges[0].nxt = head[0], which means that edges[0].nxt = -1. after that update the head to the index of this edge head[0] = 0.
Let's add the edge with index $$$1$$$ 0 3 we will update edges[1].to = 3, edges[1].nxt = head[0], which means that edges[1].nxt = 0. after that update the head to the index of this edge head[0] = 1.
Let's add the edge with index $$$4$$$ 0 2 we will update edges[4].to = 2, edges[4].nxt = head[0], which means that edges[0].nxt = 1. after that update the head to the index of this edge head[0] = 4.
Now, Can you guess how to traverse the next neighbor nodes from node $$$0$$$?
So, it's more like we push_front the edges, the new edge will point to the last edge added which is head[node], then we can update head[node] to point to the new added edge.
Next tables show the updates after adding the edges mentioned before in order.
| Updates for head array | Updates for nxt in edges array | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
..
$










