Доброго времени суток, Codeforces!
Недавно я решал задачи на структуры данных из архива, и мне пришли в голову идеи нескольких задач. Я хотел бы поделиться ими с вами и узнать ваше мнение о них. Косвенно этот блог вдохновлён похожим блогом от BERNARD. Также я буду очень рад, если в комментариях предложат решения задач (быстрее, чем за $$$O(nq)$$$) или их модификации. Любой фидбек очень важен!
В любом случае, перейдём к задачам.
Задача 1. Имеется множество из $$$n$$$ отрезков на прямой, заданных границами $$$l_i$$$ и $$$r_i$$$ ($$$0$$$ <= $$$l_i$$$ <= $$$r_i$$$ <= $$$10^9$$$). Также имеется $$$q$$$ запросов, каждый задан отрезком с границами $$$x_i$$$ и $$$y_i$$$ ($$$0$$$ <= $$$x_i$$$ <= $$$y_i$$$ <= $$$10^9$$$). Для каждого запроса необходимо найти количество отрезков, вложенных в отрезок запроса.
Задача 2. Аналогично задаче 1, но имеются запросы добавления отрезков в множество.
Задача 3. Аналогично задаче 2, но имеются запросы удаления отрезков из множества (гарантируется, что удаляемый отрезок точно есть в множестве).
Задача 4. Аналогично задаче 2, но после добавления отрезка создаётся новая версия множества и нужно в онлайне отвечать на запросы к определённой версии множества.
Задача 5. Аналогично задаче 1, но в 2D/kD (т.е. множество состоит из прямоугольников на плоскости, нужно находить количество прямоугольников на прямоугольнике).
Задача 6. Аналогично задаче 1, но вместо отрезков будем использовать простые пути в дереве, необходимо находить количество вложенных в путь запроса путей.
Задача 7. Аналогично задачам 1-4, но каждый отрезок имеет свой вес и необходимо находить не количество, а минимум/максимум среди весов вложенных отрезков.
Задача 8. Аналогично задаче 7, но нужно находить количество различных весов вложенных отрезков.
Задача 9. Аналогично задаче 7, но нужно находить медиану/k-ую статистику по весам вложенных отрезков.
Задача 10. Имеется множество из $$$n$$$ отрезков на координатной плоскости, заданных двумя точками, координаты которых не превосходят $$$10^9$$$. Необходимо отвечать на запросы количества отрезков из множества в прямоугольнике.
Задача 11. Аналогично задаче 10, но нужно уметь выполнять те же операции, что и в задачах 1-4 и 7-9.











P1. $$$\mathcal{O}((n+q)\log n)$$$, offline
Can be solved offline in $$$\mathcal{O}((n+q)\log n)$$$ using segment tree (just scale segment endpoints or use implicit segment tree). Sort queries by their starting endpoints (break ties arbitrarily). Let $$$a$$$ be an array (initially filled with zeros). For every segment $$$(l_i, r_i)$$$ increment $$$a_{r_i}$$$ by 1. Now, iterate through queries. You start at point $$$1$$$. In order to answer queries for segments $$$(1, r_i)$$$ you need to find sum $$$a_1+a_2+\dots+a_{r_i}$$$ (which can be done in $$$\mathcal{O}(\log n)$$$ using segment tree). Then, let's say there was a segment starting at $$$1$$$ and ending in some $$$r_i$$$. Obviously, it will never be in an answer to any other query, thus we can easily erase it (decrement $$$a_{r_i}$$$ by 1). Every segment will be added and removed only once thus final complexity is $$$\mathcal{O}((n+q)\log n)$$$
P2 (and also P3 actually). $$$\mathcal{O}((n+q)\log^2 n)$$$, offline
Let's take all segments and sort them by their left endpoint (break ties arbitrarily, scale them before). Now, take all segments (sorted) and create an array $$$a$$$ where $$$a_i = r_i$$$ (i.e. $$$i$$$-th element of this array corresponds to right endpoint of $$$i$$$-th segment in sorted order). Given a query $$$(l, r)$$$ we need to binary search on segments to find first segment with $$$l \leq l_i$$$ (Let's say it is $$$x$$$-th segment). The problem thus reduces to finding the number of elements less than or equal to $$$r$$$ on suffix $$$(x, \dots)$$$. You can use Wavelet tree to do the job in $$$\mathcal{O}(\log^2 n)$$$ per query so final complexity is $$$\mathcal{O}((n+q)\log^2 n)$$$.
PS. (Maybe there is a way to exploit the fact that we are doing queries on suffixes and not intervals, but I cannot think of anything clever right now).
P1-P3 can all be solved online with an ordered set on a segtree. I believe 1, 2, 3, 4, 7, 8, 9 can all be solved using 2d segtree
Задачи 1-3 решаются с помощью дерева отрезков.
Сожмем координаты. В ДО для каждой левой границы храним ordered_multiset правых (ordered_multiset можно сделать из ordered_set-a, храня пары (значение элемента, значение счетчика)). При ответе на запрос для каждой вершины ДО, полностью лежащей внутри отрезка $$$[x, y]$$$, находим количество элементов меньших либо равных $$$y$$$. При обновлениях в задачах 2 и 3 добавляем/стираем нужную правую границу на всех $$$\mathcal{O}(\log n)$$$ уровнях. Асимптотика — $$$\mathcal{O}((n + q) \log^2 n)$$$.
Или по-человечески хранить фенвик, считав все запросы в оффлайне и пожав координаты в каждой вершине ДО)
Ну и задача 5 — это просто написать трехмерное ДО)
Problem 6
The problem: for each query, find the number of fixed paths nested in the queried path.
Let's run Euler tour of the tree and record for each node $$$v$$$ the time we entered it $$$(tin[v])$$$ and the time we left it $$$(tout[v])$$$. Consider a fixed path $$$(u, v)$$$, where $$$tin[u] < tin[v]$$$ (I assume $$$u ≠ v$$$ for any fixed path).
There are 2 cases:
Case 1. $$$u$$$ is not an ancestor of $$$v$$$ (i.e. $$$LCA(u, v) ≠ u$$$). Then, any queried path that contains $$$(u, v)$$$ must start in the subtree of $$$u$$$ and end in the subtree of $$$v$$$. Note that for any node $$$x$$$ in the subtree of $$$u$$$, $$$tin[x] ∈ [tin[u], tout[u]]$$$. So $$$(u, v)$$$ will be nested in the queried path $$$(x, y)$$$ iff $$$tin[x] ∈ [tin[u], tout[u]]$$$ and $$$tin[y] ∈ [tin[v], tout[v]]$$$ or vice versa.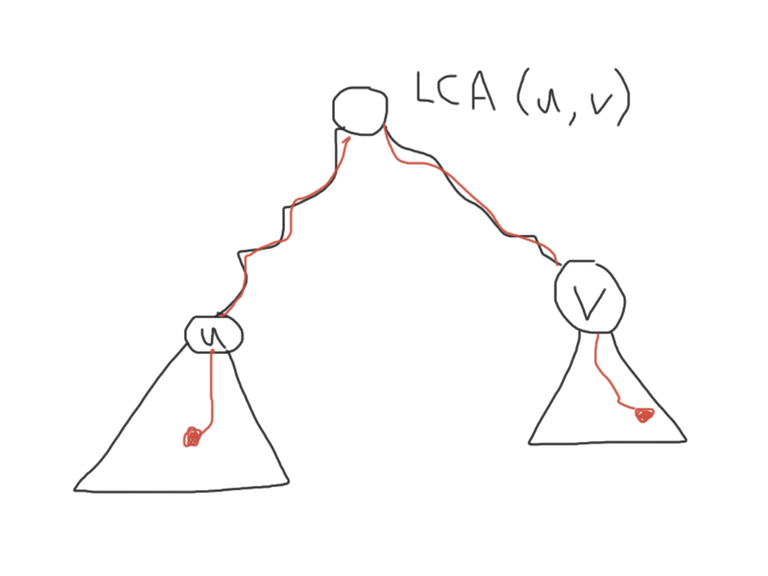
Case 2. $$$u$$$ is an ancestor of $$$v$$$ (i.e. $$$LCA(u, v) = u$$$). Let $$$w$$$ be the highest ancestor of $$$v$$$ below $$$u$$$. $$$w$$$ can be found using binary lifting in $$$O(log \;n)$$$ per path ($$$O(n \; log \; n)$$$ pre-processing is needed). It is easy to see that a queried path contains $$$(u, v)$$$ iff it starts in the subtree of $$$v$$$ and ends outside the subtree of $$$w$$$. So $$$(u, v)$$$ will be nested in the queried path $$$(x, y)$$$ iff $$$tin[x] ∈ [tin[v], tout[v]]$$$ and $$$tin[y] ∈ [0, tin[w] - 1] ∪ [tout[w] + 1, 2n - 1] $$$ or vice versa.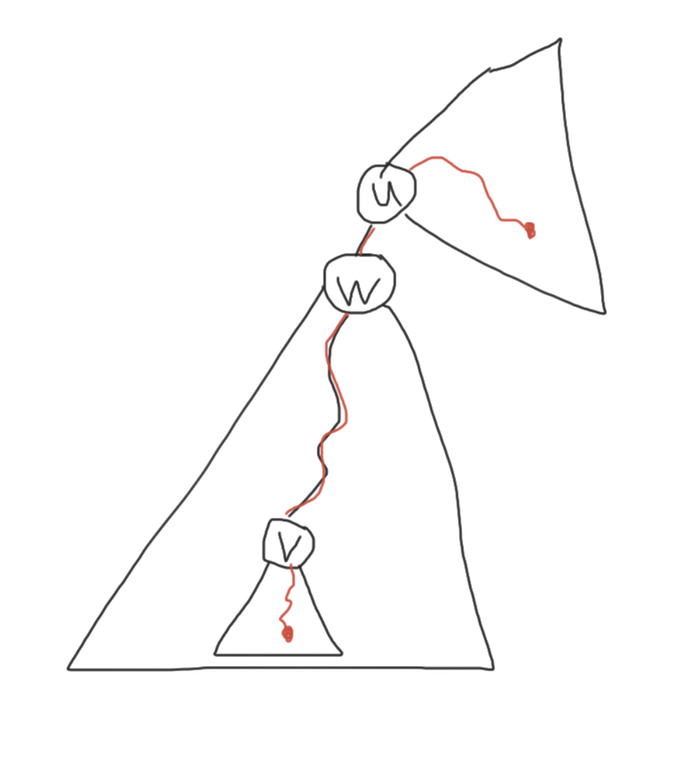
Any queried path $$$(x, y)$$$ can be represented as a point with coordinates $$$(tin[x], tin[y])$$$. Then, any fixed path creates 1 or 2 ranges for both coordinates, effectively making 1 or 2 rectangles on the plane. The answer to the query is the number of rectangles containing the queried point. This quite classical problem can be solved off-line using a difference array and a Fenwick tree in $$$O(q \; log \; n)$$$. So the total time complexity of the solution is $$$O((n + q) \; log \; n)$$$ and memory is $$$O(n \; log \;n)$$$. However, memory is $$$O(n \; log \; n)$$$ just because of the binary lifting construction, which is needed to find $$$w$$$. This subproblem is just a Level Ancestor problem and can be easily solved off-line in $$$O(n + q)$$$, e.g. by maintaining a vector of nodes on the path from the root to each vertex, so the needed $$$w$$$ can be accessed by a single array index in $$$O(1)$$$. This optimization would reduce memory complexity to $$$O(n)$$$.
See the code of the unoptimized $$$O((n + q) \; log \; n)$$$ solution below: