Sorry for the late editorial. May this editorial help you. If you have questions, feel free to ask.
The minimal weight is at least $$$1$$$ since $$$1$$$ divides any integer (so $$$1$$$ divides $$$p_1$$$).
Since $$$k+1$$$ does not divide $$$k$$$, a permutation with weight equal to $$$1$$$ is: $$$[n,1,2,\cdots,n-1]$$$.
#include <bits/stdc++.h>
using namespace std;
void work()
{
int n;
cin>>n;
cout<<n<<' ';
for (int i=1;i<n;i++)
cout<<i<<' ';
cout<<endl;
}
int main()
{
int casenum=1;
cin>>casenum;
for (int testcase=1;testcase<=casenum;testcase++)
work();
return 0;
}
See the party as a graph.
Divide the vertices into two categories according to their degrees' parity.
Let's consider the case where $$$m$$$ is odd only, since if $$$m$$$ is even the answer is $$$0$$$.
Assume that you delete $$$x$$$ vertices with even degrees and $$$y$$$ vertices with odd degrees.
If $$$y \geq 1$$$, then only deleting one vertex with an odd degree would lead to a not worse answer, so you do not need to consider it except for $$$(x,y)=(0,1)$$$.
If $$$y=0$$$, then the parity of the edges at the end is determined only by the number of edges whose both endpoints are deleted. In particular, there must be at least two adjacent vertices deleted with even degrees. So you do not need to consider it except for $$$(x,y)=(2,0)$$$ and they are neighbours.
Thus, an optimal solution either has $$$(x, y) = (0, 1)$$$ or $$$(x, y) = (2, 0)$$$ and the two vertices are adjacent.
One can iterate over all possible solutions with such a structure and take the optimal one.
Total time complexity: $$$O(n+m)$$$.
#include <bits/stdc++.h>
using namespace std;
#define MAXN 100010
int x[MAXN],y[MAXN],a[MAXN],degree[MAXN];
int n,m;
void work()
{
cin>>n>>m;
for (int i=1;i<=n;i++)
{
degree[i]=0;
cin>>a[i];
}
for (int i=1;i<=m;i++)
{
cin>>x[i]>>y[i];
degree[x[i]]++;
degree[y[i]]++;
}
int ans=INT_MAX;
if (m%2==0)
ans=0;
for (int i=1;i<=n;i++)
if (degree[i]%2==1)
ans=min(ans,a[i]);
for (int i=1;i<=m;i++)
if (degree[x[i]]%2==0 && degree[y[i]]%2==0)
ans=min(ans,a[x[i]]+a[y[i]]);
cout<<ans<<endl;
}
int main()
{
int casenum=1;
cin>>casenum;
for (int testcase=1;testcase<=casenum;testcase++)
work();
return 0;
}
The picture must consist of some stripes with at least $$$2$$$ rows or at least $$$2$$$ columns.
When $$$n$$$ is odd and all $$$\lfloor \frac{a_i}{m} \rfloor=2$$$, we cannot draw a beautiful picture using row stripes.
Let's first prove hint1 first.
If there is a pair of toroidal neighbors with different colors. For example, $$$col_{x,y}=a$$$ and $$$col_{x+1,y}=b(a\neq b)$$$. Then we will find $$$col_{x-1,y}=col_{x,y+1}=col_{x,y-1}=a$$$,$$$col_{x+2,y}=col_{x+1,y+1}=col_{x+1,y-1}=b$$$ must hold. Then we find another two pairs of toroidal neighbors $$$col_{x,y+1},col_{x+1,y+1}$$$ and $$$col_{x,y-1},col_{x+1,y-1}$$$. Repeat such process, we will find the boundary should be like:
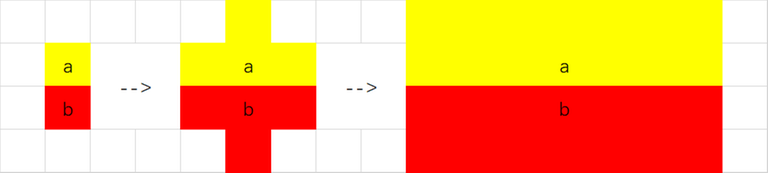
Similar, the boundaries can be vertical lines, but horizontal lines and vertical lines can not exist in one picture.
So the pattern should be row stripes all with at least $$$2$$$ rows or column stripes all with at least $$$2$$$ columns.
Check if one can draw a beautiful picture with row stripes only or with column stripes only. We consider only the case of row stripes, the reasoning is analogous for column stripes.
If it is possible, then $$$\sum_{a_i \geq 2m} \lfloor \frac{a_i}{m} \rfloor \geq n$$$ must hold.
If $$$n$$$ is even, then such a condition is enough.
If $$$n$$$ is odd, there must be some $$$\lfloor \frac{a_i}{m} \rfloor \geq 3$$$. In this case, you can draw a beautiful picture using such algorithm:
Sort $$$a_i$$$ from large to small.
Draw $$$2$$$ rows stripes of each color if possible.
If the picture still has some rows empty, insert new rows into each stripe.
Total time complexity: $$$O(n)$$$.
#include <bits/stdc++.h>
using namespace std;
#define MAXN 100010
int n,m,k;
int a[MAXN];
void work()
{
cin>>n>>m>>k;
for (int i=1;i<=k;i++)
cin>>a[i];
bool flag;
long long tot=0;
flag=0;
tot=0;
for (int i=1;i<=k;i++)
{
if (a[i]/n>2)
flag=1;
if (a[i]/n>=2)
tot+=a[i]/n;
}
if (tot>=m && (flag || m%2==0))
{
cout<<"Yes"<<endl;
return ;
}
flag=0;
tot=0;
for (int i=1;i<=k;i++)
{
if (a[i]/m>2)
flag=1;
if (a[i]/m>=2)
tot+=a[i]/m;
}
if (tot>=n && (flag || n%2==0))
{
cout<<"Yes"<<endl;
return ;
}
cout<<"No"<<endl;
}
int main()
{
int casenum=1;
cin>>casenum;
for (int testcase=1;testcase<=casenum;testcase++)
work();
return 0;
}
The maximum can always be achieved in the center position of one day's rain.
$$$a_i$$$ is a piecewise linear function and the slope of $$$a_i$$$ will only change for $$$O(n)$$$ times.
Supposing you know an invalid position $$$j$$$ where $$$a_j>m$$$, what are the properties of a rain that, if erase, makes it valid?
Let's call position $$$j$$$ a key position if it is the center position of a rain. i.e. there exists $$$i$$$ so that $$$x_i=j$$$.
You can calculate $$$a_j$$$ for all key positions $$$j$$$ using the difference array.
Let $$$d^{1}_{j}=a_{j}-a_{j-1}$$$, $$$d^{2}_{j}=d^{1}_{j}-d^{1}_{j-1}$$$, then the $$$i$$$-th day's rain will change it as follows:
$$$d^{2}_{x_i-p_i+1} \leftarrow d^{2}_{x_i-p_i+1}+1$$$
$$$d^{2}_{x_i+1} \leftarrow d^{2}_{x_i+1}-2$$$
$$$d^{2}_{x_i+p_i+1} \leftarrow d^{2}_{x_i+p_i+1}+1$$$
This can be calculated efficiently using prefix sums.
We say that a position $$$j$$$ is valid if $$$a_j\le m$$$.
Now, consider an invalid position $$$j$$$; erasing the $$$i$$$-th day's rain will make it valid if and only if $$$p_i-|x_i-j| \geq a_j-m$$$.
One can check that the region of $$$(x, p)$$$ satisfying such an inequality is a quadrant rotated $$$45^\circ$$$ anticlockwise and translated. And in particular, even the intersections of two such regions have the same structure and can be computed easily (to avoid using floating point numbers, one can multiply all $$$x_i,p_i$$$ by $$$2$$$).
In the end, for each $$$i$$$, you only need to check whether point $$$(x_i,p_i)$$$ belongs to such region.
Total time complexity: $$$O(n\log n)$$$.
#include <bits/stdc++.h>
#define MAXN 200100
#define LL long long
using namespace std;
typedef pair<LL,LL> pll;
LL n,m;
LL x[MAXN],p[MAXN];
vector<pll> diff;
pll key;
pll getIntersection(pll p1,pll p2)
{
LL tx=max(p1.first+p1.second,p2.first+p2.second);
LL ty=max(p1.second-p1.first,p2.second-p2.first);
return {(tx-ty)/2,(tx+ty)/2};
}
void work()
{
diff.clear();
key={0,-0x3f3f3f3f3f3f3f3f};
cin>>n>>m;
m*=2;
for (int i=1;i<=n;i++)
{
cin>>x[i]>>p[i];
x[i]*=2;
p[i]*=2;
diff.push_back({x[i]-p[i],1});
diff.push_back({x[i],-2});
diff.push_back({x[i]+p[i],1});
}
sort(diff.begin(), diff.end());
LL a=0,d=0;
LL lst=0;
for (auto p:diff)
{
if (p.first!=lst)
{
a=a+(p.first-lst)*d;
lst=p.first;
if (a>m)
key=getIntersection(key,{p.first,a-m});
}
d+=p.second;
}
for (int i=1;i<=n;i++)
if (getIntersection(key,{x[i],p[i]})==pll(x[i],p[i]))
cout<<'1';
else
cout<<'0';
cout<<endl;
}
int main()
{
int casenum=1;
cin>>casenum;
for (int testcase=1;testcase<=casenum;testcase++)
work();
return 0;
}
Consider the same bit of three integers at the same time.
$$$a\bigoplus b \leq a+b$$$
Define $$$cnt_{i_1 i_2 i_3}$$$ as:
$$$j$$$th bit of $$$cnt_{i_1 i_2 i_3}$$$ is $$$1$$$ iif $$$i_1=a_j,i_2=b_j,i_3=c_j$$$
e.g. $$$a=(10)_2,b=(11)_2,c=(01)_2$$$ then $$$cnt_{110}=(10)_2,cnt_{011}=(01)_2$$$, other $$$cnt$$$ is 0.
$$$a=cnt_{100}+cnt_{101}+cnt_{110}+cnt_{111}$$$
$$$b=cnt_{010}+cnt_{011}+cnt_{110}+cnt_{111}$$$
$$$c=cnt_{001}+cnt_{011}+cnt_{101}+cnt_{111}$$$
$$$a\bigoplus b = cnt_{010}+cnt_{011}+cnt_{100}+cnt_{101}$$$
$$$a\bigoplus c = cnt_{001}+cnt_{011}+cnt_{100}+cnt_{110}$$$
$$$b\bigoplus c = cnt_{001}+cnt_{010}+cnt_{101}+cnt_{110}$$$
$$$a\bigoplus b + a\bigoplus c > b \bigoplus c \iff cnt_{011}+cnt_{100}>0$$$
similar:
$$$cnt_{101}+cnt_{010}>0$$$
$$$cnt_{110}+cnt_{001}>0$$$
then we use digit dp: $$$dp[n][i][j]$$$ means when we consider first $$$n$$$ bits, state of reaching the upper bound is $$$i$$$, state of conditions is $$$j$$$.
Enumerate $$$a_j b_j c_j$$$ for $$$j$$$ from $$$|n|-1$$$ to $$$0$$$ and make transition.
Time complexity is $$$O(2^9 |n|)$$$ where $$$|n|$$$ is the length of input.
#include <bits/stdc++.h>
#define MAXN 200100
#define LL long long
#define MOD 998244353
using namespace std;
LL dp[MAXN][8][8];
string s;
int main()
{
cin>>s;
dp[0][0][0]=1;
for (int i=0;i<s.size();i++)
for (int mask1=0;mask1<8;mask1++)
for (int mask2=0;mask2<8;mask2++)
{
dp[i][mask1][mask2]%=MOD;
for (int m=0;m<8;m++)
{
bool flag=false;
for (int j=0;j<3;j++)
if (s[i]=='0' && (mask2>>j)%2==0 && (m>>j)%2==1)
{
flag=true;
break;
}
if (flag)
continue;
int tmpmask1=mask1;
int tmpmask2=mask2;
for (int j=0;j<3;j++)
if (s[i]-'0'!=((m>>j)&1))
tmpmask2|=(1<<j);
for (int j=0;j<3;j++)
if (m==(1<<j) || m==7-(1<<j))
tmpmask1|=(1<<j);
dp[i+1][tmpmask1][tmpmask2]+=dp[i][mask1][mask2];
}
}
LL ans=0;
for (int i=0;i<8;i++)
ans+=dp[s.size()][7][i];
cout<<ans%MOD<<endl;
return 0;
}
Thank dario2994, the key part of the proof is from him.
If interval $$$A,B$$$ are all good and $$$A \cap B \neq \emptyset$$$, then $$$A \cap B$$$ is good, too.
If interval $$$A,B$$$ are all good and $$$A \cap B \neq \emptyset$$$, then $$$A \cup B$$$ is good, too.
Consider enumerating good intervals according to their length.
Let's consider the interval in the order of its length (small to large) and add the edge one by one.
Initially, the graph has no edge. There are $$$n$$$ connected components each consisting of exactly one vertex. Note our algorithm will guarantee that at every moment every connected component's indices compose an interval. Let $$$[L_i,R_i]$$$ be the connected component vertex $$$i$$$ in.
If $$$[x,y]$$$ is good and $$$x$$$ and $$$y$$$ are not in the same connected component, we can merge $$$[L_x,R_y]$$$ into a larger connected component.
Supposing $$$[L_x,R_y]$$$ consist of $$$k+2$$$ connected components now, let's call them $$$[l_0,r_0],[l_1,r_1],\cdots,[l_{k+1},r_{k+1}](x\in [l_0,r_0],y\in [l_{k+1},r_{k+1}])$$$, you can link edges like:
$$$ \cdots-l_4-l_2-x-y-l_1-l_3-\cdots$$$
If $$$[x,y]$$$ is good and $$$x$$$ and $$$y$$$ are in the same connected component, then we do nothing.
Finally, you will get a valid tree.
Total time complexity: $$$O(n^2)$$$.
Let $$$ans[x][y]$$$ be if interval $$$[x,y]$$$ is good as the input data demands.
Let $$$res[x][y]$$$ be if interval $$$[x,y]$$$ is good in our answer tree.
Assume that the intervals we have considered are consistent with the input and we are considering $$$[x,y]$$$. Let's first prove if $$$ans[x][y]=1$$$ then $$$res[x][y]=1$$$.
If interval $$$x,y$$$ are in different connected components when $$$[x,y]$$$ is enumerated.
The edge-link method will ensure $$$[x,y]$$$ is good in our answer tree.
If interval $$$x,y$$$ are in the same connected components when $$$[x,y]$$$ is enumerated.
Since $$$[x,y]$$$ has been merged into a larger connected component, then there must be a series of good intervals:
$$$I_1,I_2,\cdots,I_k,I_{i+1} \cap I_i \neq \emptyset,I_i \cap [x,y] \neq \emptyset, [x,y] \subset \cup I_i$$$
Let $$$J_i=I_i \cap [x,y]$$$
Then according to hint1, all $$$J_i$$$ is good. $$$J_{i+1} \cap J_i \neq \emptyset, \cup J_i =[x,y]$$$
Then we know $$$[x,y]$$$ is good in our tree, too.
Let's then prove if $$$ans[x][y]=0$$$ then $$$res[x][y]=0$$$.
Assume that we are processing the interval $$$[x, y]$$$ and up to now we did not create an invalid interval. I will prove that even after "connecting" $$$[x, y]$$$ it still remains true that bad intervals are not connected.
Let $$$I=[a,b]$$$ not be connected before performing the operation on $$$[x, y]$$$ and become connected later. Let CC be "connected component".
Case1: $$$I$$$ does not contain $$$x$$$ or does not contain $$$y$$$, and at least one of $$$a,b$$$ is in $$$(R_x,L_y)$$$.
When $$$a,b$$$ are in different CC, $$$I$$$ does not contain both of $$$x$$$ and $$$y$$$ while they are the key vertices to walk from CC $$$i$$$ to CC $$$i+1$$$.
When $$$a,b$$$ are in the same CC, the link will have no influence on its connectivity.
Case2: $$$I$$$ contains $$$[x,y]$$$.
If $$$[a,b]$$$ becomes connected after the linking, since we only add edges in $$$[x,y]$$$, $$$[a,x]$$$ and $$$[y,b]$$$ must be connected.
Since $$$[a,x],[x,y],[y,b]$$$ are all good, $$$[a,b]$$$ is good and we are happy.
case3: $$$b \leq R_x$$$ or $$$a \geq L_y$$$.
$$$I$$$'s connectivity will not be influenced.
The proof is rather long and hard, and if you have some better ideas please share them.
#include <bits/stdc++.h>
using namespace std;
#define MAXN 5100
typedef pair<int,int> pii;
int n;
char good[MAXN][MAXN];
int lv[MAXN],rv[MAXN];
vector<pii> ans;
void work()
{
ans.clear();
cin>>n;
for (int i=1;i<=n;i++)
{
lv[i]=rv[i]=i;
cin>>(good[i]+i);
}
for (int len=2;len<=n;len++)
for (int l=1;l<=n+1-len;l++)
{
int r=l+len-1;
if (good[l][r]=='1' && lv[l]!=lv[r] && rv[l]!=rv[r])
{
ans.push_back({l,r});
vector<int> tmp[2];
int id=1;
tmp[0].push_back({l});
tmp[1].push_back({r});
for (int i=rv[l]+1;i<lv[r];i++)
if (lv[i]==i)
{
ans.push_back({tmp[id].back(),i});
tmp[id].push_back(i);
id^=1;
}
int lm=lv[l];
int rm=rv[r];
for (int i=lm;i<=rm;i++)
{
lv[i]=lm;
rv[i]=rm;
}
}
}
for (auto p:ans)
cout<<p.first<<' '<<p.second<<endl;
}
int main()
{
int casenum=1;
cin>>casenum;
for (int testcase=1;testcase<=casenum;testcase++)
work();
return 0;
}
Since they are very smart, they know the result of the game at the beginning.
If the result is $$$x$$$, then Alice will end the game when Bob moves to a cell with score less than $$$x$$$, and something analogous holds for Bob.
Thus, Alice can only move to a certain subset of cells, and the same holds for Bob.
Knowing the above facts, it is clear that we can apply binary search on the answer $$$Z$$$, which is less than $$$a_1+b_1$$$, or Alice can end the game immediately to get $$$a_1+b_1$$$.
Let's color white all the cells with $$$a_r+b_c \leq Z$$$, and black all the cells with $$$a_r+b_c > Z$$$.
Then we shall add edges between cells in the same row or same column with different colors. These edges and cells form a bipartite graph.
Consider the game on the bipartite graph. Initially, we are at cell $$$(1,1)$$$. Alice moves first, then they take turns to move. Each player can only move the cell to another place with an edge connecting them, or the other player will end the game immediately.
Each cell can be visited at most $$$1000$$$ times, whoever cannot move loses.
If Alice wins, then the answer is no greater than $$$Z$$$, otherwise, the answer is greater than $$$Z$$$.
The version of this game where each vertex can be visited exactly once is known. If both players play optimally, the first player wins iff the starting vertex belongs to all possible maximum matchings. I'll explain why at the end of the editorial.
It turns out that the condition is exactly the same even if each vertex can be visited at most $$$1000$$$ times. Let us show why.
First, calculate the maximum matching. Then we erase the starting vertex and calculate the maximum matching in the new graph. If two matchings have the same size, the vertex does not belong to all maximum matchings and vice versa.
Now, we know that if we copy a cell $$$1000$$$ times and copy the edges as well, this problem is exactly the same as the model mentioned above. If we consider the initial bipartite graph, it's easy to see that we only need to check whether $$$(1,1)$$$ is in all maximum matchings of the initial graph, because the maximum matching remains unchanged in the other $$$999$$$ parts.
So, we have shifted the problem to see if the initial cell belongs to all matchings.
According to [Kőnig's theorem in graph theory](https://en.wikipedia.org/wiki/K%C5%91nig%27s_theorem_(graph_theory)), the size of the maximum matching is equal to the size of the minimum vertex cover. And if you erase all vertices in the minimum vertex cover, you get an independent set, which is the maximum independent set.
Using $$$M$$$ to refer to the maximum matching, $$$I$$$ to refer to the maximum independent set, $$$V$$$ to refer to the set of vertices, we know that $$$|M|+|I|=|V|$$$
So, if we erase one vertex and $$$|M|$$$ remains unchanged, then $$$|I|$$$ must be changed and vice versa.
Now our issue is to calculate the maximum independent set in this graph, with or without the initial cell.
Let us sort $$$a_i$$$ and $$$b_i$$$ (notice that reordering rows and columns do not change the game at all). Now the white cells form a "decreasing histogram". We can still find the starting cell $$$(va,vb)$$$.
First, let's compute the maximum independent set with the initial cell.
Before that, consider the following constraints:
It's obvious that one column has at most one color of its cells in the independent set(we shall call it $$$I$$$), so does a row. Let's call a column white if only white cells of it are in $$$I$$$, otherwise, we shall call it black.
What is the maximum size of $$$I$$$, when we must have $$$i$$$ white columns and $$$j$$$ white rows? The answer is simple. We shall select the first $$$i$$$ columns to be white and the first $$$j$$$ rows to be white, the rest of the columns and rows to be black. Then the independent set consists of black cells on black rows and black columns, and white cells on white columns and white rows. It's easy to prove this greedy strategy is correct.
Now we fix the number of white columns as $$$i$$$, and try to find a $$$j$$$ that maximizes $$$|I|$$$. If we make an array $$$da[i]$$$ satisfying $$$a_i+b_{da[i]}\leq Z$$$ and $$$a_i + b_{da[i]+1} > Z$$$, and a similar array $$$db[j]$$$, we can easily calculate the change of $$$|I|$$$ when we turn row $$$j$$$ from black to white and vice versa, which is $$$n-max(i,db[j])-min(i,db[j])$$$, $$$-min(i,db[j])$$$ means remove the white part from $$$I$$$, $$$+n-max(i,db[j])$$$ means add the black part to $$$I$$$. For a fixed $$$i$$$, it's easy to see that the change increases with $$$j$$$.
So you can maintain all positive changes of $$$|I|$$$, just decrease the $$$j$$$ with $$$i$$$ decreasing. Now you can calculate the maximum of $$$|I|$$$ in $$$O(n+m)$$$ time.
It's easy to see that $$$da[i]$$$ and $$$db[i]$$$ are non-increasing, so they can be calculated in $$$O(n+m)$$$ time.
For the maximum independent set without the initial cell, you just need to remove it when it is in $$$I$$$. Since the cell is always black, it is quite easy.
Using binary search on the answer, you can solve the whole problem in $$$O((n+m)\log A+n\log n+m\log m)$$$, where $$$A$$$ is the maximum value of the arrays $$$a$$$ and $$$b$$$.
Let us conclude with the idea of the known game on bipartite graphs.
\textbf{Lemma}: The first player can win if and only if all possible maximum matchings include the initial vertex $$$H$$$.
Let's prove it when $$$H$$$ satisfies the constraint.
The first player can just choose any matching $$$M$$$ and move to the vertex $$$P$$$ matching with current vertex, then any unvisited neighbor of $$$P$$$ still matches with other unvisited vertices. If $$$P$$$ has a neighbor unmatched in a certain matching $$$M$$$, we find an augmenting path and a matching $$$M'$$$ that doesn't include $$$H$$$, which is in conflict with the constraint. So no matter how the second player chooses to move, the first player always has a vertex to go after that.
Otherwise, we add a vertex $$$P$$$ with the only edge $$$(P,H)$$$, move the initial cell to $$$P$$$, swap the two players, then it turns into the situation above.
#include <bits/stdc++.h>
using ll=long long;
using std::cin;
using std::cerr;
using std::cout;
using std::min;
using std::max;
template<class T>
void ckmx(T &A,T B){
A<B?A=B:B;
}
const int N=2e5+7;
int n,m,va,vb;
int a[N],b[N];
int da[N],db[N];
bool check(int x){
ll sm=0,f1=0,f2=0;
for(int j=m,i=0;j>=1;--j){
while(i<n&&a[i+1]+b[j]<=x)
++i;
db[j]=i;
sm+=db[j];
}
for(int i=n,j=0;i>=1;--i){
while(j<m&&a[i]+b[j+1]<=x)
++j;
da[i]=j;
}
f1=f2=sm;
for(int i=n,j=m;i>=1;--i){
sm-=min(j,da[i]);
sm+=m-max(j,da[i]);
ckmx(f1,sm);
ckmx(f2,sm-(i<=va&&j<vb));
while(j&&min(db[j],i-1)<=n-max(db[j],i-1)){
sm-=min(db[j],i-1);
sm+=n-max(db[j],i-1);
--j;
ckmx(f1,sm);
ckmx(f2,sm-(i<=va&&j<vb));
}
}return f1==f2;
}
void Main(){
cin>>n>>m;
for(int i=1;i<=n;++i)
cin>>a[i];
for(int j=1;j<=m;++j)
cin>>b[j];
va=a[1],vb=b[1];
std::sort(a+1,a+n+1);
std::sort(b+1,b+m+1);
int l=a[1]+b[1],r=va+vb;
va=std::lower_bound(a+1,a+n+1,va)-a;
vb=std::lower_bound(b+1,b+m+1,vb)-b;
while(l<r){
int mid=(l+r)>>1;
if(check(mid))
r=mid;
else
l=mid+1;
}cout<<l<<"\n";
}
inline void File(){
cin.tie(nullptr)->sync_with_stdio(false);
#ifdef zxyoi
freopen("my.in","r",stdin);
#endif
}signed main(){File();Main();return 0;}










Auto comment: topic has been updated by Rhodoks (previous revision, new revision, compare).
Auto comment: topic has been updated by Rhodoks (previous revision, new revision, compare).
Thanks !
Thank you for the editorial!
You don't deserve the downvotes man :(
Upvoting this Blog can decrease his negative contribution.
Let me be a snob and point out that this mathematically means it will become worse
The editorial is very well done, with hints/proofs of statements etc.
Why do we need to sort array in 1710 A? It works fine without it
it is just a way to give a valid answer. There may be better ways and in this problem you in fact do not need to implement it.
Great Div.1 D. If there had been a normal E, it would have been the best contest this month (so far).
Really liked the idea behind Div. 2 D, and the editorial explains it very well. Thanks!
Really? For me it reads like explaining nothing, just stating some formulars. I am lost in the second line.
the same
Div2 B,I spent a full hour and a half thinking about the y=0 case and did it wrong!The torial is like a drop of holy water on my rusty brain feel so good~
Can someone explain in a little more detail Div 1 C?
Is there an error in Div2 D's solution? I think it should be pi−|xi−xj|>=aj−m
you are right. Thank you very much.
I have fixed it.
Auto comment: topic has been updated by Rhodoks (previous revision, new revision, compare).
I don't understand the idea of difference array for Div2D. Can anyone explain in an easier way?
a[i] can also be calculated in this way.
Firstly,we make the contributions two arithmetic sequences.
for example x=6,p=5
that's 1,2,3,4,5 for [2,6] and 4,3,2,1 for [6,10].
then we divided the contribution of an arithmetic sequence into two parts: b+k*i
for the above examples
we add -1 for each position i [2,6],then increase each position i [2,6] by i.
we add 11 for each position i [7,10],the decrease each position i [7,10] by i.
now let's find two arrays for both the b and i.
it's easy to calculate a 1D difference array.
Thank you so much for your reply. However, if you loop through each position i in [2,6] or [7,10], will that not make your runtime O(n^2)?
well,for a arithmetic sequence,we divided its contribution into two parts.
the first part is add a number b to an interval [l,r], you can use difference array to maintain it.
the second part is add i for position i within interval [l,r] ,You can calculate how many times a position i is added,then it becomes add 1 to an interval [l,r]
Oh, I think I see what you're saying now. Thank you!
But isn't the constraint on range of x and p too high. How are u supposed to calculated difference array like this without iterating over the complete range atleast once?
just discretization.
Rhodoks orz
In Div 1C, there's an equivalent condition for the inequalities,
from the identity $$$x + y = (x \oplus y) + 2(x \land y)$$$.
So, the three satisfy the triangle inequality iff $$$a \oplus b$$$, $$$b \oplus c$$$ and $$$c \oplus a$$$ are all pairwise non-disjoint.
A digit DP solution from here is rather straightforward, 165666080.
Here's $$$\land$$$ and $$$\oplus$$$ refer to bitwise AND and XOR respectively.
Yeah I did this. The editorial soln has $$$2^9$$$ constant factor but this soln took only $$$2^6$$$.
Not really, you have atmost $$$8$$$ transitions from each state so it's more or less the same constant factor.
oops, sorry. you're right.
Can you please explain your dp states and transitions in brief?
Rather than calling the numbers $$$a, b, c$$$ let's call them $$$x_0, x_1, x_2$$$.
We iterate from the highest bit to the lowest, so call the highest bit $$$0$$$.
We have the states $$$(\text{idx}, \text{tight}, \text{cond})$$$ where $$$\text{idx}$$$ is the current bit we are on, $$$\text{tight}$$$, and $$$\text{cond}$$$ are bitmasks of size $$$3$$$.
$$$\text{tight}_i$$$ is set if $$$x_i$$$ currently matches the input on the prefix $$$[0, \text{idx})$$$.
$$$\text{cond}_i$$$ is set if $$$(x_i \oplus x_{i + 1}) \land (x_i \oplus x_{i - 1})$$$ (the indices are modulo $$$3$$$) has a bit set among the $$$[0, \text{idx})$$$ bits.
I believe the transitions should be clear if you have experience with digit DP.
We finally require that $$$\text{cond}_0, \text{cond}_1, \text{cond}_2$$$ are set so the final answer is $$$\sum_i \text{dp}(\lvert n\rvert, i, 7)$$$.
what does "all pairwise non disjoint" mean?
By disjoint I mean that $$$x \land y = 0$$$, because if you view $$$x$$$ and $$$y$$$, as bitmasks/sets, $$$x \land y$$$ is the intersection of $$$x$$$ and $$$y$$$, and we say that sets $$$S$$$ and $$$T$$$ are disjoint if $$$S \cap T = \varnothing$$$.
So $$$x, y, z$$$ being pairwise non-disjoint means that $$$x \land y$$$, $$$y \land z$$$ and $$$z \land x$$$ are all non-zero.
As a member of botswana community, i upvoted this post !!!!!!!!!!!!
Why does this solution give the wrong answer? http://pastebin.ubuntu.com/p/TrRV4gSKG5/
Just look at the solution in tutorial for problem A. It's much more simple.
Your code fails when n = 8. Output is 8 7 6 5 4 3 2 1 but 6 % 3 = 0.
i divides pi means that pi % i = 0, not the other way round.
For 1710B-Rain, why will the maximum position always be one of the centers? Can anybody help me to prove that?
A point $$$p$$$ which is between two center points, $$$L$$$ is all the points locates left to it and $$$R$$$ is all the points locates right to it. When we move $$$p$$$ from left to right, the rainfall from $$$L$$$ decrease(getting far away from it) or stay the same(some points is too far to give rainfall), the rainfall from $$$R$$$ increase or stay the same. In detail, the rainfall from $$$L$$$ decrease quickly first, then slowly(some points becomes too far) and the rainfall from $$$R$$$ increase slowly first, then fast(some points becomes close enough). That is the second derivative is always non-negative. So one of the center point must be the maximum point.
This makes so much sense. Thanks a lot :)
Can someone help me understand the solution of div1B? I do not understand the implementation of the logic given in the editorial. What exactly is getIntersection() calculating?
I just finished writing this huge post trying to explain it the best way I found. Hopefully it will answer some of your questions.
I struggled a lot with understanding how we found the intersections in 1710B — Rain without doing exhausting casework, so I decided to explain the math in the code for anyone else who also had a hard time.
We will keep track of the region $$$S$$$ such $$$\forall (x, p)\in S$$$ then there is no flood, i.e $$$p - |x - j| \geq a_j - m$$$, for all invalid positions $$$j$$$.
Looking at the inequlity ( we can see that $$$(x,p)\in S \iff p\geq |x-h|+c$$$ (as mentioned in the editorial "One can check that the region of $$$(x,p)$$$ satisfying such an inequality is a quadrant rotated $$$45^\circ$$$ anticlockwise and translated.")
So we will keep track of a function $$$f(x) = |x-h| + c$$$ to keep track of the region. Initially the center of a region described by point $$$j$$$ is $$$(j, a_j - m)$$$ so $$$h = j$$$, $$$c = a_j - m$$$ (notice that point $$$(h,c)$$$ is the center of such a region). Now $$$(x,p)\in S \iff p \geq f(x)$$$
Now how can we interesect two regions $$$S_1,S_2$$$ described by $$$f_1, f_2$$$? We need to find the function $$$f_3 = \max(f_1, f_2)$$$. By visualizing (or doing a bit more complex case work) we can see that $$$S_3 = S_1 \cap S_2$$$ is also described by a similar function $$$f_3(x) = |x-h_3| + c_3$$$. How will we figure the parameters?
If $$$x\leq \min(h_1,h_2)$$$ then $$$f_3(x) = \max(f_1, f_2) = \max(h_1 + c_1 - x, h_2 + c_2 - x) = t_x - x$$$ $$$(I)$$$ ($$$t_x$$$ is defined like that in the code).
If $$$x\geq \max(h_1,h_2)$$$ then $$$f_3(x) = \max(f_1, f_2) = \max(c_1 - h_1 + x, c_2 - h_2 + x) = t_y + x$$$ $$$(II)$$$ (again $$$t_y$$$ is defined in the code).
As we mentioned $$$f_3(x) = |x-h_3| + c_3$$$ so if $$$x\leq h_3$$$ then $$$f_3(x) = c_3 + h_3 - x$$$ and because of $$$(I)$$$, particularly looking for $$$x\leq \min(h_1, h_2, h_3)$$$ it must hold that $$$h_3 + c_3 = t_x$$$. Doing the same for $$$x\geq h_3$$$ because of $$$(II)$$$ we see that $$$c_3 - h_3 = t_y$$$. Solving the linear system we see that $$$(h_3,c_3) = \left(\frac{t_x-t_y}{2}, \frac{t_x + t_y}{2}\right)$$$. Which are the parameters for region $$$S_3$$$.
In that way we can find the region $$$\displaystyle S = \bigcap_j S_j$$$ (going through all the invalid positions $$$j$$$) which was what we wanted to find.
There might be an easier way but it is the most intuitive way I could find to understand the solution.
i think we can calculate intersection directly. suppose we have two region specified by $$$(a,b)$$$ and $$$(c,d)$$$ , and the intersection is $$$(x,y)$$$. then because the boundaries of regions are just line with slope 1 or -1, we can get
which gives
through my test, it seems the same as the one in tutorial code
That may be the case for some situations but the formulas are not correct every time. That is why my goal in the post was to skip "exhausting casework".
Consider two points which sit on the same horizontal line, specifically $$$(a, b)$$$ and $$$(c,d) = (a, d)$$$. Then the formulas give the intersection as $$$(x,y) = \left(\frac{2c+d-b}{2}, \frac{b+d}{2}\right)$$$. We can see how this is not correct since the we can easily see that the center point should be $$$(x,y) = (a,b)$$$. (suppose $$$b>d$$$)
Note: you might argue that we never intersect points with the same $$$x$$$ value, so with some constraint the problem may be solved the way you described but it is not whole picture I wanted to give.
oh, well, you are right. the main reason is that when one region totally contain another region, the intersection assumed in my equation is actually not exist.
so it can not achieve "check whether point (xi,pi) belongs to such region", but just calculate some "ideal" intersection ... QAQ
hello, after calculating the prefix and suffix sums and getting the total rainfall in all xi's, why can't we do an O(n^2) approach, where we go through each day and get the maximum after removing that day's rain and checking if it is <= m ? , i tried it but gave me WA in TC2 , can you tell me why my approach would be wrong?
if we put time complexity aside, your method is absolutely right.
however this problem has no guarantee about input xi and pi, so there may be some cases that many pairs of same xi and pi, and your 'originalPos' only record one position. if there are more than one feasible solutions among them, you just change one position in answer string.
one possible work around is use map<pair, queue> , you can refer to this
meanwhile, i don't understand very well how you calculate 'left' and 'right' arrays , could you explain a little
okay i assumed xi's are always unique my bad, so i think there's an easier way to pre calculate the sums but for me the motivation was, for each xi (consider sorted pair<xi,ai> and the rainfall can extend only to the right of xi), it will be
left[i]=a[i]+max(0,left[i-1]-valReduce[i]- cnt*abs(x[i]-x[i-1])),
now what is cnt? cnt should ideally be the number of rains that have happened before x[i] (in terms of the number-line) but that does not happen as some rainfall might not extend till the current x[i] hence at every iteration for left prefix i check the max index to which i can extend my current rainfall to, and to the next index of that (redxnIndex) i increase cntReduce array so that when i arrive at that index i know i will need to reduce my cnt by this and also add some correction value to the above equation to valReduce array , similarly i do the same for right and then get the tot[i]=left[i]+right[i]-rainfall[i]
so it will take O(N*log(N) + N) to calculate the total rainfall after N days
also according to the constraints shouldn't O(N^2) run in 4 seconds? just curious
thanks for explanation.
for time issues, firstly based on system test result we know it can't pass. then from my experience, if a problem is tend to be solved by a n^2 solution, the N is at most around 1e4.
Let's upvote this editorial to show some support to Rhodoks.
Can someone help me figure out what's wrong with my submission for C 165672596
What my function does is that it divides all the elements in a by m. I then make me a list of all the elements in a that are greater than or equal to 2 and also find their sum. If this sum is less than the number of rows, return false. If it is equal to the number of rows, return true. Now we know that the number of rows we can use is greater than n. First go through all the elements of the list we created. If we can erase all the rows from the current color and still have our sum greater than or equal to n, we'll remove it. Else, we'll calculate the amount of rows from which we can safely remove from the color. This is basically the total amount of rows from that color minus 2. This amount is nonnegative because all the elements of the lest are greater than or equal to 2. We'll use as much of this leftover as possible and decrease sum and the current color by this leftover. At the very end, if the sum is equal to the number of rows, return true else return false.
Just call this function twice(swap the row and col the second time). If at least 1 returns true, then the answer is Yes. Otherwise the answer is obviously No.
As you can probably tell, this problem frustrated me a lot in contest. I'm wondering if anyone has a testcase or logic flaw that breaks my solution.
Take a look at Ticket 15920 from CF Stress for a counter example.
Thanks a lot!
Here is a test-case:
First color fills 3 rows, while the rest each fill 2 rows. The YES solution is simple: use 3 + 2 = 5. However, your approach calculates a sum of 3 + 2 + 2 + 2 = 9. Then the first iteration of the leftover loop checks if 3 can be dropped, concluding that yes, 3 can be dropped to reduce the sum to 6, and it also changes the 3 to 0. However, without the 3, it is impossible to reach a target value of 5, since all that's left are 2s.
Even aside from this, I don't feel like your approach of calculating leftovers and adjusting the sums accordingly is guaranteed to reach a correct solution, especially since the loop doesn't revisit a color (just a plain for loop). Have you actually proved anything about this approach?
Instead, consider this alternative observation: if we overshoot the target, then for each color that covered more than 2 rows, we can decrease how many rows it covers (don't implement this, just think). If you keep reducing the problem in this manner, what are the possible outcomes? Is there some state that can't be reduced in this manner, but still overshoots? Once you characterize this state, you should be able to figure out when such a state can lead to a YES and when it will lead to a NO.
You beat me to it.
yeah, thanks. It's obvious to me now that a constructive solution like mine would be harder to make work.
Say your list is [3,2,2,2] and you are trying to make 5. You algorithm will take 1 out of the 1st element, and report 'No'?
I like how we both thought of literally the exact same counterexample
Is there a proof of Hint 2 from XOR Triangle Editorial ?
a XOR b <= a + bFor each bit, XOR is the plus modulo $$$2$$$ which is less or equal to plus.
In div 2 problem c my logic is same as given in this editorial but still it shows wrong answer on test 8 . Here's my solution https://codeforces.net/contest/1711/submission/165574557 Please help!!!
Oh, your ll is just long but not long long.
So it will overflow.
wow, the relation between div2D and region intersections is beyond my thought, interesting.
To be honest, apart from Div. 1 E, this is a really great round. The questions are really well-thought.
Thank you for this round.
Question not that related to this round: Was problem difficulty rating system different in the past? I found lot of problems that have very high difficulty rating for it's difficulty. Some of them are from like 10 years ago, but some of them like this one is from 3 years ago.
i like the problems a lot ty <3
The editorial of Div2B (1711B) is a little misleading:
In particular, specifying the conditions of $$$y \geq 1$$$ and $$$y = 0$$$ (which are mutually exclusive conditions) suggests that these are two mutually exclusive cases to consider, i.e., if $$$y \geq 1$$$, we should only consider the odd degrees for removal, while the removal of adjacent vertices with even degree should only be considered when $$$y = 0$$$. But this is false, since even when $$$y \geq 1$$$, it is not enough to consider only the odd vertices, and the optimal solution may require the removal of two adjacent even vertices instead.
My suggestion would be to remove all mention of $$$x$$$ and $$$y$$$ (since their values are irrelevant for the algorithm design), and instead phrase these "cases" as options to consider (the I/O explanation in the problem also refers to them as options), with a brief note of why it's sufficient to only consider these two options: the other options not considered are the removal of a single even person only (which doesn't fix the total degree parity) or the removal of some superset of one of these two options (odd + some set, or even + even + some set).
well said
Well, what I want to express is that, if you have an answer:
If $$$y \geq 1$$$, you can get a not worse (but may not be the best) answer by only deleting one odd degree vertex of the $$$y$$$ vertices. So you do not need to consider it except when $$$(x,y)=(0,1)$$$.
If $$$y = 0$$$, you can get a not worse (but may not be the best) answer by only deleting two adjacent even-degree vertices. So you do not need to consider it except when $$$(x,y)=(2,0)$$$ and they are neighbours.
So, If we want to find the best answer, we only need to consider such two cases as I said.
And if you think what I express here is easier to understand, I will modify it.
cough it's totally not because I suck at graphs that I ruined my ratings this round cough it shouldn't be violent cough
A different solution to Div1 D:
$$$Construct(L,R)$$$ is a function that finds the edges in the component of [L,R] ([L,R] is connected).
You can construct as follows:
Let $$$z$$$ be the largest number satisfies $$$z<R$$$ and $$$[L,z]$$$ is connected.
Let $$$x$$$ be the largest number satisfies $$$x\leq z$$$ and $$$[x,R]$$$ is connected.
There is a useful property :
Then if you construct $$$[L,z]$$$ first , the only influence to $$$[L,R]$$$ are the segments $$$[y,R],(L\leq y\leq z)$$$
If $$$[z+1,R]$$$ is connected then the rest of construction is easy:
If $$$[z+1,R]$$$ is not connected . Then $$$[z+1,R]$$$ can be split into some connected components $$$[l_1,r_1],[l_2,r_2]...[l_k,r_k],[l_{k+1},r_{k+1}]$$$.
The solution is also not hard:
$$$Construct[l_i,r_i]$$$ for every $$$i$$$.
Connect $$$r_1,r_2,r_3...r_{k-1}$$$ and $$$R$$$.
Connect $$$r_k$$$ and $$$x$$$.
Connect $$$R$$$ and $$$x$$$.
In fact the last two part can be implemented together.Submission: 165734051
I get stuck proving only stripe pattern make all cell to have at least 3 neighbors. (Div.2 C)
Is there a easy way to prove it?
In other words, if the picture is not a stripe, there must be a place which has $$$2$$$ neighbors with different colors.
neighbors with different colors are blacken.
1 1 1 1
1 1 2 2
2 2 2 2
Node that the lenth / width of the stripes mush be bigger than $$$2$$$.
thank's for your reply.
i proved this by different way!
we can generalize "non stripe pattern" as a "(stripe pattern) — (hole)" when hole is not stripe.
and there is a two case.
holes appear in first column.
no hole appears in first column.
1st case ex)
xxxxxx
001000 <- 1 in this column is bad
010000
110011
010001
(x is color which is not 1 (possibly 0))
then
-> there exists always bad color 1 in column which color 1 is appear for the first time.
2nd case ex)
xxxxxx
111111
111111
010000 <- some 0 in this column is bad
110011
010001
then
-> there exists always bad color 0 in column which color 0 is appear for the first time.
and this model include all possible region -> proved!
oH mine gods, Sparky_Master_WCH1226 are the goodest in contributon rateing agan. thakns for you suppot sar.
D2D
Damn. This getIntersection magic is the one I wouldn've thought about.
You can do it simpler. Just maintain the minimum height current point should have to "cover" all the things on the left of it. It is a very simple dp.
Then calculate the same for right and check for each point whether it satisfies both left and right.
Hello. Can someone tell me please, why this solution for C is WA?
https://codeforces.net/contest/1711/submission/165895290
Thank you!
UPD: Got it: https://codeforces.net/contest/1711/submission/165896780
Take a look at Ticket 15939 from CF Stress for a counter example.
I already found mistake, but anyway thank you!
Getting MLE in Problem B (Party). My solution
How to resolve?
move the FastIO out of the while loop https://codeforces.net/contest/1711/submission/165923134
Thanks a lot ! Btw what fast input output really did there? to give a mle ... can you explain :).
tbh i have no idea lol sorry :(.
It's fine ..you solved my problem anyways.
For 1710A-Color the Picture, shouldn't $$$\sum_{i=1}^{n} \lfloor \frac{a_{i}}{m} \rfloor$$$ instead be $$$\sum_{i=1}^{k} \lfloor \frac{a_{i}}{m} \rfloor$$$? Also, I don't understand why if, when $$$n$$$ is even, $$$\sum_{i=1}^{k} \lfloor \frac{a_{i}}{m} \rfloor \geq n$$$ is sufficient. What if every $$$a_{i}$$$ was a single row? Don't you still check if you can make the sum using at least $$$2$$$ from each? It should be the sum of every $$$\lfloor \frac{a_{i}}{m} \rfloor$$$ that is at least $$$2$$$.
You are right, It is $$$k$$$ and I forget to mention skipping those $$$a_i < 2*m$$$.
I solved Div1B in incredibly ugly way using segment tree. It was good exercise though.
I also tried an approach with a seg tree but couldn't figure it out. If you have time, could you please explain how you did it?
Let $$$T(x)$$$ be the total accumulation at position $$$x$$$. We can compute a bunch of intervals $$$[l_{i},r_{i})$$$ and pairs of integers $$$(a_{i},b_{i})$$$ such that for all $$$x\in[l_{i},r_{i})$$$, $$$T(x)=a_{i}x+b_{i}$$$ using prefix sum technique. If we let $$$f_{i}=\max_{x\in [l_{i},r_{i})} a_{i}x+b_{i}$$$ then it is obvious that we will get $$$f_{i}$$$ either at $$$x=l_{i}$$$ or $$$x=r_{i} - 1$$$. Now we want to consider the case when we can erase the $$$j$$$ th rain. After we erase the rain, if we let $$$W_{j}(v)$$$ be the total accumulation of the position $$$v$$$ if we erase $$$j$$$ th rains, then:
Notice, that for every $$$i$$$, $$$\max_{v\in [l_{i},r_{i})} W_{j}(v)$$$ will also be achieved at either $$$v=l_{i}$$$ or $$$v=r_{i}-1$$$. Thus, all we have to do is compute the maximum of $$$W_{j}(v)$$$ for all $$$v\in [l_{i},r_{i})$$$ for each $$$i$$$ using segment tree and compare the maximum with $$$m$$$. (Forgive me for terrible explanation because it is quite difficult to explain in plain English which is not my mother tongue)
That was a really good explanation, thanks a lot!
I was having hard time figuring out the editorial soln for Div2D/Div1B. So this is what I came up with.
First we figure out all the $$$a_i$$$ values as stated in the editorial. We will only consider all the $$$x$$$ values for which $$$a_{x} > m$$$. Call them critical points.
Take a look at the $$$i$$$-th flood. We will check it's left and right side separately. For it to fix any point $$$j$$$ to it's left (that is $$$j < x_i$$$), this must be true: $$$a_j - (p_i - |x_i - j|) \leq m$$$ $$$\Rightarrow a_j - j - m \leq p_i - x_i$$$. Deletion of $$$i$$$-th flood must satisfy this for all critical points to it's left. Here we can keep prefix maximum for $$$a_j - j - m$$$ for all critical points and compare that with the R.H.S.
We can get similar equation for the right half. It's $$$a_j + j - m \leq p_i + x_i$$$. This can be checked by keeping suffix maximums for all critical points.
Overall the solution will be $$$\mathcal{O}(n\log{}n)$$$. One note for implementation, it's easier to check the two equations for all relevant points (even ones with $$$a_x <= m$$$) instead of just the critical ones. For points with $$$a_x <= m$$$ define their L.H.S of the two above equations to be $$$-\infty$$$ and it will be fine. Here is my submission.
arman_ferdous how is it handling the points to the left of the ith flood for which pi<xi-j?
In div1C, can anyone explain how the transitions are taking place? What is
mand how does it decidetmpmask1andtmpmask2?$$$m$$$ is the $$$i$$$-th bit of $$$a,b,c$$$. For example, when $$$m=(101)_2$$$ then $$$a_i=1,b_i=0,c_i=1$$$.
First, you should check if $$$m$$$ is valid for the current state. If $$$cnt$$$ will let $$$a,b,c$$$ exceed the upper bound you should "continue".
Then $$$tmpmask2$$$ is whether it will reach the upper bound ($$$0$$$ is yes while $$$1$$$ is no). $$$tmpmask1$$$ is whether it satisfies the conditions we mention in the editorial ($$$1$$$ is yes while $$$0$$$ is no).
The editorial of 1E says:
(And it mistakes "because" for "becuase".)
I think it's not obvious (probably because I'm too foolish), so I try to prove it. We need to prove
The main idea of my proof is to prove that there exists no augmenting path in the two matchings we get above. To prove this, we assume that there exist an augmenting path, and we try to make it contains no more than one copy of any vertices. Then we show that this path is an augmenting path of the maximum matching of the initial graph or the initial graph without $$$(1,1)$$$.
Sorry for not writing the whole proof down here, but my poor English doesn't allow me to do that.
However, since the editorial said "it's easy to see", I believe there is a much cleverer and shorter proof. But I'm not able to come up with it. If anyone knows the proof, please teach me. Thanks.
And the editorial says
Note that if $$$da_{va}=da_{va-1}$$$ or $$$db_{vb}=db_{vb-1}$$$ ($$$(va,vb)$$$ is the starting cell), this strategy may not give the correct result for a certain $$$(i,j)$$$. I don't know whether it can always give the correct maximum independent set.
I'm too lazy to write the proof for why it's correct if $$$(va,vb)$$$ doesn't meet this condition, but it's not hard to prove.
Actually, I think you can get WA depending on how you implement it.
Let $$$s(i,j), i \in [0,n], j \in [0,m],$$$ denote the size of the independent set if we pick the first $$$i$$$ rows and $$$j$$$ first columns white. Let $$$db[j]$$$ be the number of white cells in each column. Note that $$$db[j]$$$ decreases with $$$j$$$. Then, (when the initial position is considered black)
That means that it is useful to increase $$$j$$$ if $$$\delta(i, j) > 0 \iff db[j] > n - i$$$. On the other hand, if $$$db[j] = n-i$$$, then we get the same size of independent set whether or not we increase $$$j$$$. Thus, you could implement it such that you increment $$$j$$$ whenever $$$db[j] >= n-i$$$ or whenever $$$db[j] > n-i$$$ and both would be correct when the initial position is considered black. However, when the initial position is not considered black, for some $$$j$$$ the condition becomes $$$db[j] > \text{or} >= n - i - 1$$$. Let us see that if you pick the strict option, $$$db[j] > n - i$$$, your code gives WA.
Suppose $$$n = 4, m = 2$$$ and that the matrix is as follows, where X marks the initial position.
Then, $$$db[] = {2,2}$$$. For $$$i = 0$$$, $$$db[0] = 2$$$ is smaller than $$$n - 0 = 4$$$, so the optimal $$$j$$$ is $$$0$$$ and $$$s(0,0) = 3$$$ because the starting point is not considered black. The same happens when $$$i = 1$$$. When $$$i = 2$$$, though, $$$n - i = 2$$$ and $$$db[0] = 2$$$. Hence, if we increase $$$j$$$ we still have the same maximum independent set size. But, once we do so, the condition becomes $$$db[j] >= n - i -1$$$, meaning that it is strictly better to increase $$$j$$$. The optimal $$$j$$$ for $$$i = 2$$$ is $$$j = 2$$$. This corresponds to choosing all white cells as independent set, giving answer $$$4$$$. They key fact is that if we don't increase $$$j$$$ when the answer would not improve, we don't get to this position.
It is true that in this example the same position would be obtained when $$$i = 3$$$, but I think that we can craft examples where this does not happen.
To remember this easily, the mental heuristic would be to prefer maximum independent sets with more white vertices, since afterwards there is a black vertex that we are going to remove if it is in our independent set.
In fact, I have just checked so with two different submissions.
Strict Comparison WA8
Non-strict Comparison AC
Can anyone explain me Question B — Rain. I'm unable to understand the editorial.
Which part do you need to explain? Difference and prefix sum? Or the calculation of region?
Please explain calculation of region part?
First, the maximum of $$$a$$$ can always be achieved at the center of a certain rain. So if for the center position of any rain $$$j$$$, $$$a_j \leq m$$$ then we know it is valid.
If $$$a_j > m$$$ then if erasing rain $$$i$$$ can make position $$$j$$$ valid, $$$p_i−|x_i−j| \geq a_j−m$$$ must hold. Let's see what such a region is like.
$$$p_i−|x_i−j| \geq a_j−m \iff |x_i-j| \leq p_i+m-a_j$$$ where $$$m-a_j$$$ is known constant for a certain $$$j$$$.
So point $$$(x_i,p_i)$$$ should be in such a region:
$$$-p_i-C_1 \leq x_i-C_2 \leq p_i + C_1$$$
Which is the translation of region $$$-p_i \leq x_i \leq p_i$$$, like:
Multiple such regions' intersection still holds such structure, and it can be easily calculated. I think UUUnmei's picture shows it clearly.
You can refer to my
getIntersectionfunction which uses a way of rotation (rotate 45° clockwise and take the maximum of $$$x,y$$$ then rotate them back) to calculate it.So much thanks for this wonderful explanation.
What topic should know first to understand the solving approach/ solution of problem D:Rain?
I think you need to understand difference and prefix sum. You can refer to this link.
In this problem, you need a "second difference" and calculate it after discretization.
Well, so finally Rhodoks' contribution turns positive again. That is a fair result at last anyway. Congratulations again, and also %%% CCOrz.
Alternate solution to problem 1710B Rain which does not requires you to find intersection: The idea is similar to this problem. First calculate value of a at all points then calculate the equivalent points. Then take their range. For any valid point it must cover the entire range.
AC Submission
In 1710C if we use a "magic" array t={0,1,2,4,4,2,1,0} (each element means that if the i-th bit of a,b,c is m, then t[m] is the "condition mask" of the condition m will satisfy), we could make it's code simpler than the official solution.
My submission:189673909