Centroid Decomposition of a tree

11 years ago, # ^ |

But that is HLD :(

→ Reply

zeulb

11 years ago, # |

← Rev. 3 →

+21

I'm not sure what this technique called, but this seems to be a divide and conquer approach http://www.ioi2011.or.th/hsc/tasks/solutions/race.pdf , i think it's possible to decompose the tree using this, although i have never try it

EDIT: I found this page explaining some tree decomposition technique and tree data structure (i think), the page is in japan, but some have english reference (there's also paper explaining centroid decomposition, i think this might be helpful)

→ Reply

11 years ago, # ^ |

← Rev. 3 →

Thanks, I think I am beginning to get the whole picture here. :)

So, you find the centroid of a tree, mark it as a special node and root the tree in the centroid. After removing that centroid node, you end up with a forest. Now, find the centroid of each component(and mark them as special nodes) and continue till you have completely decomposed the tree.

Now, if you consider the original tree(rooted at its centroid) with the nodes marked special or not, note that for any node, if you traverse the path to the root, there are at most (log n) special nodes.

So, we are storing information about the whole tree in the special nodes. Each special node contains some information about its subtree. And we have to appropriately modify the special nodes for each update and use the information stored in the special nodes for each query.

I hope I am right so far. If so, someone please tell me what information we are storing, by taking an example problem, say SPOJ QTREE5 and I hope it will become clear to me :)

Edit: This is not quite right, Check out Zlobober's comment below.

→ Reply

11 years ago, # ^ |

It was called "divide and conquer by node" in one CF problem. But it's not suitable for query-update problems, because it processes each subtree in the decomposition in linear time. It's good for problems like the IOI one, and can be replaced with HLD.

→ Reply

11 years ago, # ^ |

I'm not sure that it can always be replaced with HLD.

For example, problem from one of Summer Petrozavodsk camp 2013 contests: we have the tree with nodes numerated from 1 to N. Initially we are standing at the node 1. On each turn we are moving to the most distant node from the position we are standing currently (if there are several of them, to the one with maximal number) and delete (previously) current node. The task is to find the sequence of node numbers we will visit.

I only know how to solve this problem with divide-and-conquer approach.

→ Reply

11 years ago, # ^ |

Well, there may be problems where that idea fails. It's hard to say (but probably not as hard as with P=NP? :D). Still, it works in most cases, and HLD is more suited as an answer to the thread question, because it can be used with update/query problems easily, like with "BIT over HLD".

→ Reply

11 years ago, # ^ |

← Rev. 2 →

I know that HLD can do most tree query-update problems, but it is a pain to code(at least, for me). In codeforces Round 225, I tried to code it for Propagating tree but failed miserably.

Also, there is no harm in learning new stuff, useful or not. On the contrary, it is fun. :D

→ Reply

11 years ago, # ^ |

← Rev. 2 →

Constructing HLD is just DFS, where you pick the path that the current node belongs to. It can be used in a complicated way, but for most problems, it's just one while-loop.

You can't immediately code everything perfectly — try to successfuly code it for some problems, and it'll be much easier next time.

→ Reply

11 years ago, # ^ |

You are right, that was a lame excuse. :P But I actually coded HLD successfully once. The HLD part was indeed simple but I was stuck in the update and query part, but that was not because HLD is hard, it just reflects my general coding skills :(

But well, there are other good things about learning new stuff. It gives you confidence, for example, and sometimes help you figure out the solutions for difficult problems like that Summer Petrozavodsk camp 2013 problem. Of course you know all this(as you have done several difficult problems) but I am just merely pointing out that the thread question was specifically about centroid decomposition :D

→ Reply

11 years ago, # ^ |

My original point when mentioning HLD was along the lines of: if you want an update/query structure, then centroid decomposition will hardly help. But yeah, it's good to know both.

→ Reply

11 years ago, # ^ |

Hah, this problem was on finals of Algorithmic Engagements in 2013 (which I have pariticipated in :) !) and nobody has solved it (although there were some great coders for example Tomek Czajka!). I don't know a solution with divide-and-conquer, but main idea of a solution proposed by author (dasko1) was maintaining a middle-point of diameter and some funny operations using interval trees :p.

→ Reply

11 years ago, # ^ |

+29

I can explain solution for this problem.

Divide-and-conquer idea is pretty simple. Let's find the center of the tree, make it root, and call it a layer. Then we delete the root and recursively call this procedure from all remaining subtrees, producing second order layers, third order and so on. Since each time we are making the center of the tree to be the root, on each iteration all remaining subtrees have size not greater than the half of initial size, so there will be logarithmic depth of recursion.

Here is the simple, but not fully optimal idea for the solution. For each layer let's write all vertices in an array in order of DFS. Let's try to answer next query. Suppose we currently stay in vertex x. x is a member of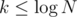 $\text{[math]}$ layers L₁, L₂, L₃, ... L_k (starting from the deepest, i. e. smallest one). Let's suppose that the most distant vertex is y. Let's find first layer L_d, that contains both x and y. Then the path $\text{[math]}$ contains the root of layer L_d, so its length is $\text{[math]}$ . 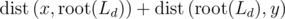So the idea how to find y becomes clear. Let's iterate over all layers, containing x, (suppose we have precalculated distance from x to all roots of layers containing him), and now we should find the most distant vertex y from another subtree of the root (not containing x itself). That can be done, if we store not a usual array for that layer, but, for example, segment tree containing maximums. The we can easily extract maximal possible distance from the root (excluding the segment containing vertices of our subtree) with y producing that distance. Iterating over all layers we find the best y, make x = y and totally delete old x from the structure.

It is solution in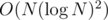 $\text{[math]}$ time. Further possible optimizations are removing one of 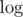$\text{[math]}$ factors through storing vertices not in segment tree, but in order of increasing their distance to the root and moving some pointers.

→ Reply

11 years ago, # ^ |

Thanks, I think I got it.

My previous post about centroid decomposition was wrong(except for the first paragraph). But your explanation is pretty good.

Here is how one would solve QTREE5, hopefully it is correct. Do the centroid decomposition and for each layer, store the set of white vertices for that layer in the root. Also, for each node, store an array marking the list of layers it is a part of and other similar bookkeeping stuff(I haven't coded it yet and so I am not sure if this is all the things we need to store).

Then, the update is just modifying the set of white nodes for each of the $\text{[math]}$ layers. For the query, go to each layer and get the shortest white node from the root in that particular layer and find the distance. The overall complexity would be $\text{[math]}$

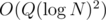
Since we are finding the nearest white node, it does not matter if the current node we are querying is in the same subtree as the shortest node(the better distance would have been precomputed earlier). Otherwise we would need some segment tree stuff like Zlobober mentioned above.

The most important(also obvious) fact here is that for any two vertices, if we consider the smallest layer containing them, then the path between these two vertices contains the root of that layer. :D

→ Reply

7 years ago, # ^ |

-7

How are the operations on the Centroid Decomposition (CD) of a tree linked to the original tree? Because, CD of a tree is a completely new tree. Distance between a pair of vertices A and B in the CD of a tree can be distinct from the distance between them in the original tree.

→ Reply

satyaki3794

7 years ago, # ^ |

Yes, you are right. You need to use the formula dist(A, B) = depth(A)+depth(B)-2*depth(LCA(A,B)) to get the distance when considering pairs of nodes in the centroid tree.

→ Reply

7 years ago, # ^ |

Yes it's the length of the paths(A, C) and (C, B). But this is the distance in the centroid decomposition. How about the distance in the original tree given two vertices A and B? I assume both the queries and updates are asked to be performed on the original tree. We are just making use of CD. So there must be a direct mapping between original and CD tree. In other words, how the results of queries on CD interpreted as final answer to the query to original tree?

→ Reply

satyaki3794

7 years ago, # ^ |

dist(A, B) is with respect to original tree, not CD. If A and B are in diff subtrees of the centroid C, the distance bw them in the original tree is dist(A, C) + dist(B, C).

→ Reply

7 years ago, # ^ |

← Rev. 3 →

Suppose that you're given a tree like a linked list: 1->2->3-> ... -> 15. The distance between 1 and 7 is 6 in the original tree. Now the centroid decomposition is as follows:

          8
         / \
        4   12
       / \    \ ... leaving this subtree
      2   6
     / \ / \
     1 3 5  7

Depth(1) = 3, depth(7) = 3, LCA(1, 7) = 4, depth(4) = 1. The distance between 1 and 7 in centroid decomp. is as follows: depth(1) + depth(7) - 2 * depth(4) = 3 + 3 - 2*1 = 4. But in the original tree it was 6. Dist(1, 7) = 6 != 4

→ Reply

satyaki3794

7 years ago, # ^ |

dist(A, B) is with respect to original tree, not CD

depth(1)=0, depth(7)=6, LCA(1,7)=1, so dist = 0+6-2*0 = 6

→ Reply

7 years ago, # ^ |

Where and how do we use CD then?

→ Reply

PrakharJain

7 years ago, # ^ |

We used CD in figuring out how to break the required path into it's 2 parts and for preprocessing the answers for every centroid to its component path. Rephrasing, finding the LCA for the given nodes, and then breaking the query is done from the CD tree while finding the actual answer for a particular part is done using the original tree. At last, that's what we actually wanted.

→ Reply

rhezo

8 years ago, # ^ |

← Rev. 3 →

I can't understand the above solution(in Zlobober comment). Can anyone explain in more detail please :(

Specifically, what is a layer. And this line "Let's find first layer L_d, that contains both x and y". Why will both x and y lie in the same layer? Maybe I didn't understand the definition of a layer. I didn't read after this line.

→ Reply

11 years ago, # ^ |

I finally recognized what is "Algorithmic Engagements". In 2011 it had online mirror contest where I have also participated in. That was really great problemset, I liked it very much! But after that year there was no such online contests. Why?

→ Reply

11 years ago, # ^ |

It is a really great competition! You can access problems from old editions here: http://main.edu.pl/en/archive/pa . Eliminations have form of solving many problems during one week and the later is roung the harder are problems (and problems from group A are harder than from group B). Fun fact: TOP3 in FBHC2013 in 2/3 (Petr, meret, Marcin_smu) coincided with TOP3 from AE in PA2012 (tomek, meret, Marcin_smu) which was ~2 month earlier :P.

And I have to say that I don't know why 2011 is the only year when online contest was organized, but I have that luck that in 2010 I was too bad coder to try competing, in 2011 I participated in online contest (and performed unexpectably well :)! ) and in 2012 and 2013 I was able to qualify to finals :D.

→ Reply

11 years ago, # ^ |

Is the on-site contest only for Polish coders? Were there ever participants from other countries?

→ Reply

11 years ago, # ^ |

Yes, the whole competition (even eliminations) is purely for Poles, but maybe there is a chance that at least eliminations can be available to coders from other countries. I can ask organizers about their opinion on that.

I remember that few years ago also Ukraine was allowed to compete, but details are not clear for me and now regulations clearly state that only Poles can compete.

And necessarily watch this :D! Song about AE2009

→ Reply

King_George

8 years ago, # ^ |

-8

Hi!

I wonder where we can find this problem.

In the gym? (I don't know the exact problem id.)

→ Reply

zeulb

11 years ago, # ^ |

Is it possible to solve IOI Race using HLD ?

→ Reply

11 years ago, # |

+13

This technique is described in a statement of this problem :D 235D - Graph Game

→ Reply

halfo

11 years ago, # ^ |

"One man's problem is another man's solution" :D :D

→ Reply

11 years ago, # ^ |

Thank you, that is just a short version of the solution to IOI 2011 Race(given by zeulb) :D

→ Reply

halfo

11 years ago, # |

+20

I request you to write a blog about Centroid Decomposition with examples. So others may not have to go through all the hard works you've gone though to learn it. Thanks :)

→ Reply