Combined Questions PDF Link
Q1) Two Operations
Problem Description
Example Test Case + Explanation
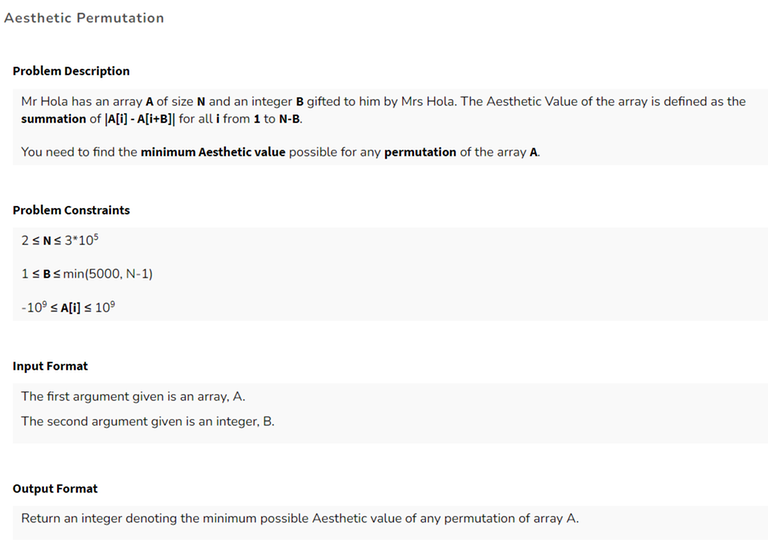
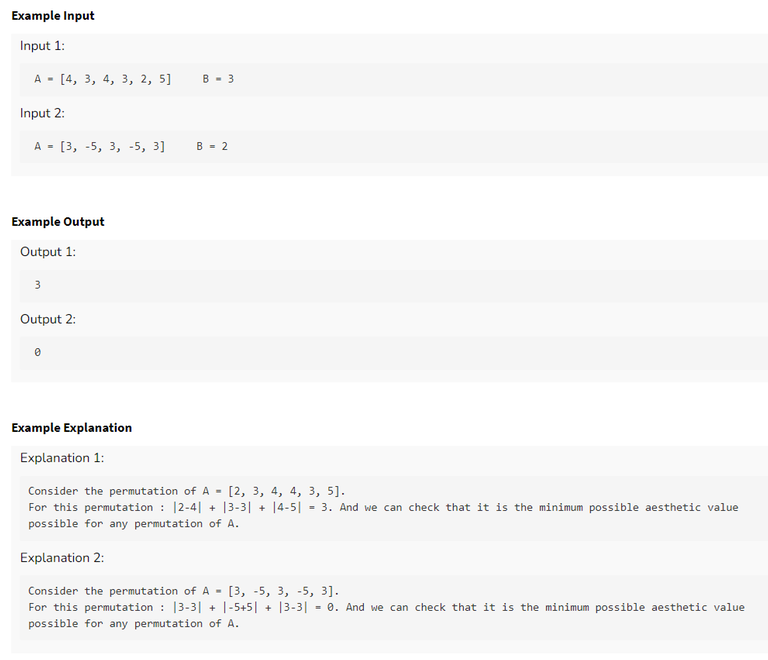
Q2) Aesthetic Permutation
Problem Description
Example Test Case + Explanation
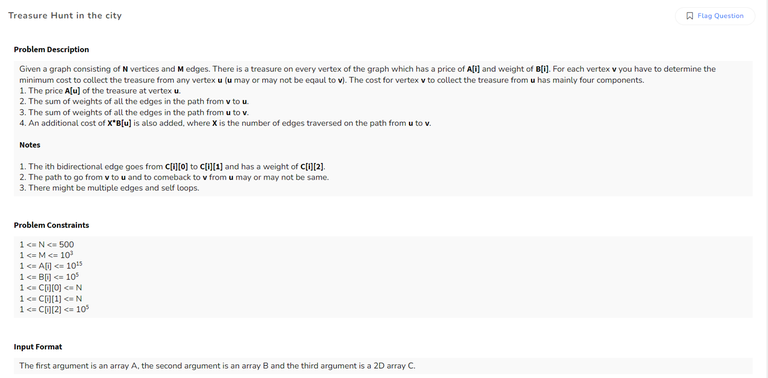
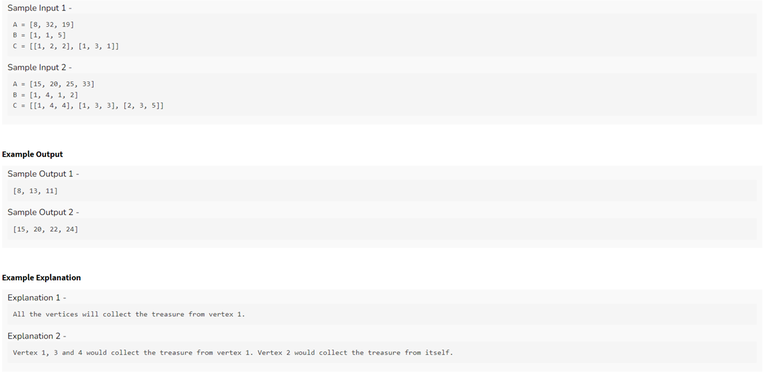
Q3) Treasure Hunt in the city
Problem Description
Example Test Case + Explanation
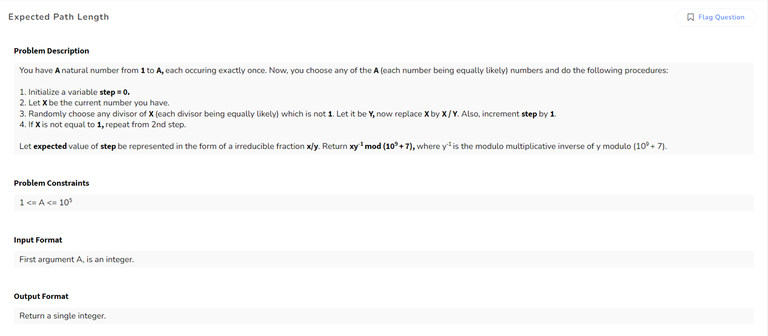
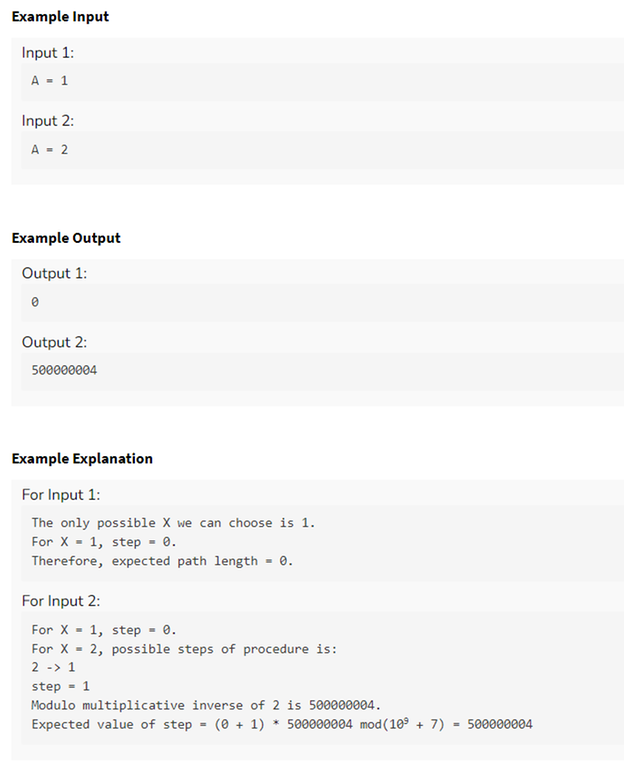
Q4) Expected Path Length
Problem Description
Example Test Case + Explanation
Q5) Intersection of segments
Problem Description
Example Test Case + Explanation
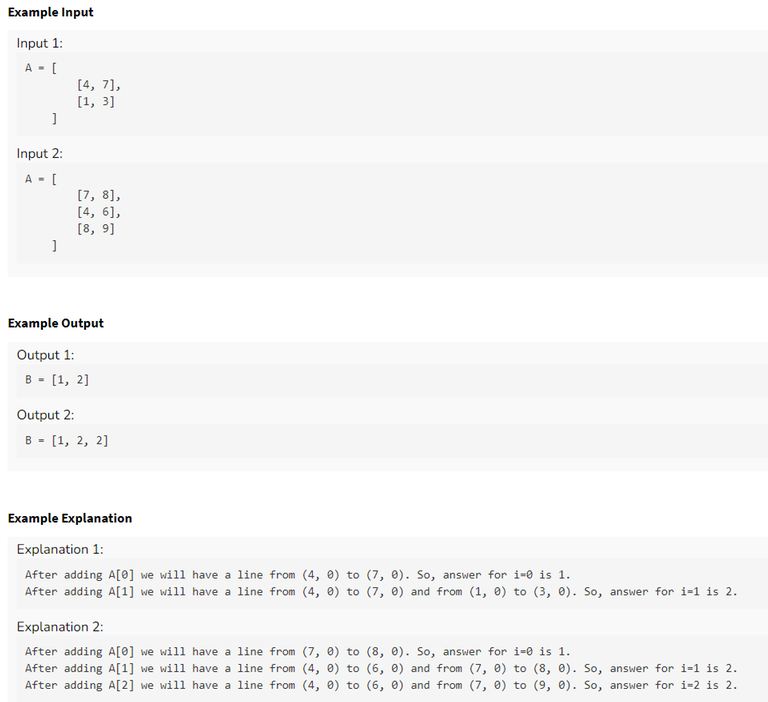
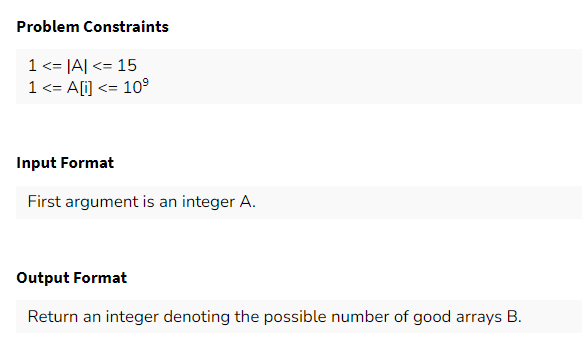
Q6) Possible Array
Problem Description
Example Test Case + Explanation
Please share your Approaches and Solution for problems in comments.
If this Discussion was Helpful, Please do Upvote this Blog for Greater Audience Reach.
Disclaimer : This Thread is made for Discussion of Codeagon-2023-Contest, which was held on 8-Jan-2023 from 12 PM to 3 PM I.S.T. The Contest has been officially Ended and this Discussion Thread is Published after the Contest.

















Appreciate your efforts. How to solve 6th?
The problem can be reduced to the number of simple paths in a graph, which is a standard dp problem
It is always optimal to change the elements to the number between the max and min of the array.
Also, it doesn't make any sense to change the elements which are not on the boundary. So we should change boundary elements first and make them closer so that we can minimize the gap between max and min elements.
Note we are given at max $$$2$$$ operations. So we are left with three possibilities to change the element.
Change the first two elements to the third element (in a sorted array).
Change the first element to the second element and change the last element to $$$2nd$$$ last element.
Change the last two elements to the $$$3rd$$$ last element.
We can separate the problem into various sequences, let's take $$$i$$$ as the starting index, then we can group index $$$i$$$, $$$i+B$$$, $$$i+2*B$$$, ... together.
There can be at max two different lengths of sequences possible. Suppose the length of the sequence starting from index $$$0$$$ is $$$x$$$ then there can be only either $$$x$$$ or $$$x-1$$$ length sequences.
Total number of such sequences will be at max $$$b$$$ because we are grouping at an interval of $$$b$$$.
The elements to be put in each of the sequences should be continuous if we don't then there will be the repetition of that range again in another sequence.
I have used $$$dp[i][j]$$$ which denotes the number of ways if we have $$$i$$$ sequences of length $$$x-1$$$ and $$$j$$$ sequences of length $$$x$$$.
Note: We don't need to store the index as we can calculate it using the value of $$$i$$$ and $$$j$$$ easily.
Now suppose I am at $$$id$$$$$$th$$$ index, then I will have two possibilities either place the next $$$(x-1)$$$ elements and use our one $$$i$$$ operation, i.e., decrease $$$i$$$ by $$$1$$$ in the transition else decrease $$$j$$$ by $$$1$$$ and place the next $$$x$$$ elements.
I tried to implement it recursively but I got MLE. So you can just write it iteratively, $$$dp[i][j]$$$ depends only on $$$dp[i-1][j]$$$ and $$$dp[i][j-1]$$$. So, we can fill the $$$dp$$$ array diagonally, i.e., based on the $$$i+j$$$ value
I could get only $$$166/300$$$. So won't comment much on this problem, you can check other's approaches :)
It was a direct problem based on the definition of expected value and dynamic programming.
$$$dp[i]$$$ denotes the expected length for number = $$$i$$$.
Base case : $$$dp[1] = 0$$$
Now expected value = $$$\sum_{}^{} p * val $$$, where $$$p$$$ denotes the probability of a particular event and $$$val$$$ is the expected value after going to that event.
Here we can go to all the divisors of $$$i$$$ except $$$i$$$, so our expression will look like :
$$$\sum_{}^{} \frac{1 \, + \, dp[factor]}{count \, of \, factors \, of \, i}$$$
There are two ways to compute the sum, one is the basic one of iterating over the square root of each number to find the factors and do the given summation. Time complexity will be $$$O(n\sqrt{n})$$$.
Another method is to use a sieve kind of iteration as the total number of factors will be $$$O(nlogn)$$$.
I coded it with $$$O(n\sqrt{n})$$$ during the contest.
Final answer would be : $$$\frac{1}{n}\sum_{1}^{n}dp[i]$$$
Keep a set of ranges in the form of a pair $$$[l,r]$$$.
Suppose you have to insert a range $$$[x,y]$$$, so you only need to update just the ranges which overlap with the current range $$$[x,y]$$$.
So you can do a binary search using $$$lower bound$$$ or $$$upper bound$$$ functions to find the start of the ranges already present in our set.
Erase all the pairs which overlap with the current range to be inserted and then insert the current range. Don't forget to update the $$$x$$$ and $$$y$$$ values as in the overlap $$$x$$$ may decrease or $$$y$$$ may increase.
You are dealing with a certain pair only twice, one while inserting and the other while deleting. You will not iterate for them more than $$$2$$$. And the number of pairs is $$$O(n)$$$, so the final time complexity will be $$$O(nlogn)$$$.
Note that the length of $$$A$$$ is at max $$$15$$$, so it can be taken as a hint to solve the problem using bitmask $$$dp$$$.
I used $$$dp[i][j][k]$$$, where $$$i$$$ denotes the current index I am at, $$$j$$$ denotes the bitmask of already taken indices from the array $$$A$$$, and $$$k$$$ is $$$0$$$ or $$$1$$$, $$$0$$$ denotes I have to place smaller element and $$$1$$$ denotes I have to place larger element.
Now the transition is easy. Let me know if you are struggling with the transitions.
I will update the solution to problem 6 in a more detailed way after some time.
Bruh How are you RED with 1800 rating xD
Because Santa is Real!!!
In problem 2nd i figured that
We have to first sort the array-
choose a (n/B) length continuous segment and put it on i ,i+B ,i+2*B ,... pos If n is not divisible by B then there are some chain of (n/B) +1 ...
So I dont know how to implement this like [len(n/B)][len(n/b +1)] .. some random order
Can you help with this idea
Implementation part or do you have any difficulty in the logic building?
I have problem in implemention But now I get it Thanks:)
Can you share your code and approach ?
I dont recall much of it. I think it has some dp implementation You check below comments there you find implementation
in 4th problem , i dit the exact same but just a small query,
dp[x] =
( 1/(total_divisor) )* ( (1 + dp[x1]) , (1 + dp[x2]) ,.... (1 + dp[x]))if we separate dp[x] , it will bedp[x] = (1/(total_divisor-1)) * ( (1 + dp[x1]) , (1 + dp[x2]), .... + (1))
I think in your solution you already mentioned that we excluded itself I am thinking the ''one'' that remains from the last block where we chooose 1 as its factor and contribute a step
//Plz check if i am wrong
Yes if we can go the same number then we will have to shift the dp(x) coefficient to LHS and then divide it. In this contest it was mentioned that we can't go to the same number.
But in today's Trilogy contest we can go to the same number so your mentioned modification should be done
ohhh i see , Thanks
Can you provide Soln of todays trilogy contest also , It would be helpfull
Do you have the pictures of the problems? Btw I could not solve the first problem completely.
I only know 1st problem statement bcz i managed to solve it , but doesn't have ss of it and other also I only have ss of this expected value question
What was your approach for the first problem? Just to confirm your first problem was that monster and hero problem?
i actually created a segtree. Then i sort the Monster array by its health Now for j in Heroes array , We find [0..i] by lower_bound such that we can remove them if they are at B[j][0]
Now by segtree , point query I store Ans[j] Which means if jth hero comes it will erase Ans[j] amount of monster
Then just update as heroes comes
I have soln also , if you want i can share that also
Oh yes! I should have thought of it.
https://pastebin.com/sW101ufx
Yes I have. Which one you need?
In Problem 6, how to keep track of last chosen index for the next transition?
Did you guys receive any acknowledgement mail (like successfully completed the test) after completion of the test? After 3hrs I was taken to a page that says couldn't access test instead of test completed page.
no
Can anyone explain solution of problem 2.
https://codeforces.net/blog/entry/111127?#comment-990186
Using linearity of expectation, Expected Value of Steps =
1 / A * (summation of Exp(x) over all 'x'), where 1 <= x <= ALet divisors(x) = number of divisors of 'x'.
Exp(x) = 1 / divisors(x) * (1 + summation of Exp(x / d) over all divisors 'd')Since A <= 10 ^ 5, it can be calculated using sieve.
Problem 3
Think about the cost for fixed vertices u and v.
All parts of the cost are independent of each other, except third and fourth part depend together on the return path.
The first part, A[u] is independent of path taken.
For second part, we must choose the path with minimum sum of weights.
The sum of 3rd and 4th part is sum of weigths in return path + no of edges in return path * B[u]. Either minimize the sum of weights or minimize the no of edges. Take the minimum of both cases.
Use Floyd-Warshall algorithm for computations.
We create the following two sets of two 2-d arrays:
dp1[i][j] = min'm sum of weights of a path b/w i and j. edges1[i][j] = no of edges in that path with min'm sum of weights.
edges2[i][j] = min'm no of edges on a path b/w i and j. dp2[i][j] = sum of weights on that path with min'm no of edges.
Between any 2 vertices i and j, the two possible costs are:
Min'm weight: A[j] + dp1[i][j] + dp1[i][j] + edges1[i][j] * B[j].
Min'm edges: A[j] + dp1[i][j] + dp2[i][j] + edges2[i][j] * B[j].
Hence, cost between two vertices i and j is minimum of both cases.
Now, we can use Floyd-Warshall Algorithm to compute the values of all four arrays in O(N^3).
After this, for every vertex i, we can iterate over all N vertices to find the one with minimum cost.
The given graph is not simple. So while constructing the initial adjacency matrix, dp and edges, you need to check for self-loops (ignore them) and multiple edges (store the one with min'm weight).
Thanks for reading! Please point out if I've made any mistake. Feel free to share any better or more interesting approach.
Were you able to get this approach accepted in the contest?
Yes.
How much problems we have to solve to get shortlisted for interviews?
Q-2 Aesthetic Permutation solution using DP:
Notice that there would be a total of b sequences of type Sequence1 -> 1, 1+b, 1+2*b ... Sequence2 -> 2, 2+b, 2+2*b ...
Now out of b, b-n%b sequence will have size of n/b and rest (n%b) will have size of n/b+1.
Each sequence should have elements in sorted form. Now dp comes into the picture to decide which sequence should get elements from current_index to current_index + (size_of_chosen_sequence)-1.
Yes bro i have the same idea but don't able to implement:( Thanks bro for your implementation
Anybody got any mail about selection? Or when is the result anybody knows?
Anyone?
Yeah got ccat link.
24 batch.
Anyone from the 2023 batch received any mail for the next steps?