Suleyman.A's blog

about infinite
By Suleyman.A, 11 years ago, In English

I wonder what the infinite is. someone say that 1^infinite = 1 we don't know what the infinite is how it can be equal to 1 and I know 1^everything is = 1
Please help, thanks.

  • Vote: I like it
  • 0
  • Vote: I do not like it

»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Reading the Wikipedia article may help better understand the concept.

As to how we may define 1∞, there's another reading there on how to define common operations on the set of real numbers extended with  ± ∞.

→ Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

If you want function 1x to be continuous in extended real number line you have to define 1x for x =  + ∞ as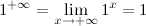 and for x =  - ∞ as .

→ Reply
»
11 years ago, # |
  Vote: I like it +16 Vote: I do not like it

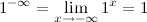This reminds me of the exponential.

Limits of "1 power infinity" expressions often yield exponential functions. For example, for any given t:

Notice that the base approaches 1 and the exponent approaches infinity, but the resulting function is something completely different — and quite interesting.

→ Reply