We hope you enjoyed these problems :) This contest has been in the works for almost a year.
This round was mostly made possible by problemsetters from the CerealCodes initiative!
CerealCodes is an organization based in the United States dedicated to running high quality competitive programming contests. You can check out our previous contest here.
UPD: D1D Editorial have been updated
UPD 2: D1D Editorial now has images by EmeraldBlock. As an apology gift for being so slow, the image generator is programmatic and available here.
1853A - Desorting
Problem Credits: buffering
Analysis: buffering
To make $$$a$$$ not sorted, we just need to pick one index $$$i$$$ so $$$a_i > a_{i + 1}$$$. How do we do this?
To make $$$a$$$ not sorted, we just have to make $$$a_i > a_{i + 1}$$$ for one $$$i$$$.
In one operation, we can reduce the gap between two adjacent elements $$$i, i + 1$$$ by $$$2$$$ by adding $$$1$$$ to $$$1 \dots i$$$ and subtracting $$$1$$$ from $$${i + 1} \dots n$$$.
It is clearly optimal to pick the smallest gap between a pair of adjacent elements to minimize the number of operations we have to do. If we have $$$a_i = x, a_{i + 1} = y$$$, we can make $$$x > y$$$ within $$$\lfloor \frac{(y - x)}{2} \rfloor + 1$$$ operations.
Thus, we can just go through $$$a$$$, find the minimum difference gap, and calculate the minimum operations using the above formula. Note that if $$$a$$$ is not sorted, we can just output $$$0$$$.
The time complexity is $$$O(n)$$$.
#include <bits/stdc++.h>
#include <numeric>
using namespace std;
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
int T; cin >> T;
while (T--) {
int n; cin >> n;
vector<int> nums(n);
int diff = 1e9;
bool sorted = true;
for (int i = 0; i < n; i++) {
cin >> nums[i];
if (i > 0) {
diff = min(nums[i] - nums[i - 1], diff);
sorted &= nums[i] >= nums[i - 1];
}
}
if (!sorted) {
cout << 0 << endl;
continue;
}
cout << diff/2 + 1 << endl;
}
}
1853B - Fibonaccharsis
Problem Credits: ntarsis30, cry
Analysis: cry
Can a sequence involving $$$n$$$, which is up to $$$10^5$$$, really have up to $$$10^9$$$ terms?
The terms of the fibonacci sequence will increase exponentially. This is quite intuitive, but mathematically, fibonnaci-like sequences will increase at a rate of phi to the power of $$$n$$$, where phi (the golden ratio) is about $$$1.618$$$. Thus, the maximum number of terms a sequence can have before it reaches $$$10^9$$$, or the maximum value of $$$n$$$, is pretty small (around $$$\log n$$$).
Instead of trying to fix the first two elements of the sequence and counting how many sequences $$$s$$$ will have $$$s_k = n$$$, note that we already have $$$n$$$ fixed. If we loop over the $$$k-1$$$th element of the sequence, the sequence is still fixed. If we know the $$$x$$$th element and $$$x-1$$$th element of $$$s$$$, we can find that $$$s_{x - 2} = s_{x} - s_{x - 1}$$$.
Thus, we can just go backwards and simulate for $$$k$$$ iterations in $$$O(\log n)$$$ since $$$k$$$ is small, breaking at any point if the current sequence is not fibonnaci-like (there are negative elements or it is not strictly increasing). Otherwise, we add $$$1$$$ to our answer.
The time complexity is $$$O(n \cdot \log n)$$$.
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int T; cin >> T;
while (T--) {
int n; int k;
cin >> n >> k;
int ans = 0;
for (int i = 1; i <= n; i++) {
int second = n; //xth element where x is k
int first = i; //fixing x-1th element where x is k-1
bool valid_seq = true;
for (int j = 0; j < k - 2; j++) {
//for s_x and s_x-1, s_x-2 = s_x - s_x-1
int fx = first;
first = second - fx;
second = fx;
valid_seq &= first <= second;
valid_seq &= min(first, second) >= 0;
if (!valid_seq) break; //break if the sequence is not fibonacci-like
}
if (valid_seq) ans++;
}
cout << ans << endl;
}
}
Bonus: Solve for $$$n, k \leq 10^9$$$
Analysis by awesomeguy856
$$$f[k] = F_{k-2}f[0]+F_{k-1}f[1]$$$
By the Extended Euclidean Algorithm, we can find one integral solution for this equation, since $$$\gcd (F_{k-2}, F_{k-1}) = 1 | f[k].$$$ Let this solution be $$$(f[0], f[1]) = (x, y).$$$ Then all other integral solutions are in the form $$$(x+cF_{k-1}, y-cF_{k-2}),$$$ for $$$c \in Z$$$ so we can find all valid solutions by binary search on $$$f[1],f[0] \geq 0$$$ and $$$f[1]>f[0]$$$, or just by some calculations.
1852A - Ntarsis' Set
Problem Credits: nsqrtlog
Suppose that the numbers are arranged in a line in increasing order. Take a look at each number $$$x$$$ before some day. If it isn't deleted on that day, what new position does it occupy, and how is that impacted by its previous position?
If $$$x$$$ is between $$$a_i$$$ and $$$a_{i+1}$$$, it will move to a new position of $$$x-i$$$, since $$$i$$$ positions before it are deleted.
Take this observation, and apply it to simulate the process backwards.
Suppose the numbers are arranged in a line in increasing order. Consider simulating backwards; instead of deleting the numbers at positions $$$a_1,a_2,\ldots,a_n$$$ in each operation, then checking the first number after $$$k$$$ operations, we start with the number $$$1$$$ at the front, try to insert zeroes right after positions $$$a_1-1, a_2-2, \ldots, a_{n}-n$$$ in each operation so that the zeroes will occupy positions $$$a_1, a_2, \ldots, a_n$$$ after the insertion, and after $$$k$$$ insertions, we will check the position that $$$1$$$ will end up at.
If $$$a_1$$$ is not equal to $$$1$$$, the answer is $$$1$$$. Otherwise, each insertion can be processed in $$$O(1)$$$ if we keep track of how many of $$$a_1-1, a_{2}-2,\ldots,a_{n}-n$$$ are before the current position $$$x$$$ of $$$1$$$; if $$$a_1-1$$$ through $$$a_i-i$$$ are before $$$x$$$, then we will insert $$$i$$$ zeroes before $$$x$$$.
The time complexity is $$$O(n+k)$$$ per test case. The editorial code additionally processes every insertion with the same $$$i$$$ value in $$$O(1)$$$, for $$$O(n)$$$ overall complexity.
There are alternative solutions using binary search with complexity $$$O(k\log nk)$$$ or $$$O(k\log n\log nk)$$$, and we allowed them to pass. In fact, this problem was originally proposed with $$$k \leq 10^9$$$ but we lowered the constraints.
#include <bits/stdc++.h>
using namespace std;
int n, k, a[200010];
void solve() {
cin >> n >> k;
for (int i = 0; i < n; i++) {
cin >> a[i];
a[i] -= i;
}
if (a[0] != 1) {
cout << 1 << "\n";
return;
}
a[n] = 2e9;
//start at position 1, and find what number moves to its position
long long ans = 1;
int inc = 1; //how many zeroes to insert
while (inc < n) {
int days = (a[inc] - ans + inc - 1) / inc;
if (days >= k){
ans += k * inc;
k = 0;
break;
}
ans += days * inc;
k -= days;
while (a[inc] <= ans) inc++;
}
ans += 1ll * k * n;
cout << ans << "\n";
}
int main() {
ios::sync_with_stdio(0);
cin.tie(nullptr);
int t; cin >> t;
while (t--) solve();
}
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int inf = 1e9+10;
const ll inf_ll = 1e18+10;
#define all(x) (x).begin(), (x).end()
#define pb push_back
#define cmax(x, y) (x = max(x, y))
#define cmin(x, y) (x = min(x, y))
#ifndef LOCAL
#define debug(...) 0
#else
#include "../../debug.cpp"
#endif
int main() {
ios_base::sync_with_stdio(0); cin.tie(0);
int t; cin >> t;
while (t--) {
ll n, k; cin >> n >> k;
vector<ll> a(n);
for (int i = 0; i < n; i++)
cin >> a[i];
ll j = 0, x = 1;
while (k--) {
while (j < n && a[j] <= x+j)
j++;
x += j;
}
cout << x << "\n";
}
}
1852B - Imbalanced Arrays
Problem Credits: nsqrtlog
You can solve the problem by picking one number from each pair $$$(n, -n)$$$, $$$(n - 1, -n + 1) \dots$$$, $$$(1, -1)$$$.
$$$b_i > b_j$$$ implies $$$a_i > a_j$$$.
First, try to determine one index in $$$O(n)$$$, or determine if that's impossible.
Sort the array $$$a$$$ to optimize the $$$O(n^2)$$$ solution.
At the start, let $$$x$$$ be an index such that $$$b_x$$$ has the greatest absolute value. If $$$b_x$$$ is negative, we have $$$a_x=0$$$, and else $$$a_x=n$$$. Moreover, we can't have $$$a_y=0,a_z=n$$$ for any indices $$$y$$$ and $$$z$$$, because that implies $$$b_y+b_z$$$ is both positive and negative, contradiction. Hence, the necessary and sufficient condition to check if we can determine an element in array $$$b$$$ with maximum absolute value is (there exists an element of array $$$a$$$ equal to $$$0$$$) xor (there exists an element of array $$$a$$$ equal to $$$n$$$). Then, we can remove that element and re-calculate the $$$a$$$ array, leading to an $$$O(n^2)$$$ solution. If the check fails at any moment, there is no valid solution.
To optimize it further, note that we can sort array $$$a$$$ at the start and keep track of them in a deque-like structure. We only need to check the front and end of the deque to see if our key condition holds. Finally, we can use a variable to record the number of positive elements deleted so far and subtract it from the front and end of the deque when checking our condition, so that each check is $$$O(1)$$$. The overall complexity becomes $$$O(n\log n)$$$ due to sorting.
#include <bits/stdc++.h>
using namespace std;
int n, ans[100010];
vector<pair<int,int>> arr;
void solve() {
cin >> n;
arr.resize(n);
for (int i = 0; i < n; i++) {
cin >> arr[i].first;
arr[i].second = i;
}
sort(arr.begin(), arr.end());
int l = 0, r = n - 1, sz = n;
while (l <= r) {
if ((arr[r].first == n - l) ^ (arr[l].first == n - 1 - r)) {
if (arr[r].first == n - l) {
ans[arr[r--].second] = sz--;
}
else {
ans[arr[l++].second] = -(sz--);
}
}
else {
cout << "NO" << "\n";
return;
}
}
cout << "YES" << "\n";
for (int i = 0; i < n; i++) cout << ans[i] << " ";
cout << "\n";
}
int main() {
ios::sync_with_stdio(0);
cin.tie(nullptr);
int t; cin >> t;
while(t--) solve();
}
1852C - Ina of the Mountain
Problem Credits: fast-fourier-transfem
Analysis: fast-fourier-transfem, EmeraldBlock, GusterGoose27
Suppose you knew in advance how many times each octopus will regenerate. Could you solve the problem then?
To make things easier, replace health values of $$$k$$$ with health values of $$$0$$$, so the goal is to reach $$$0$$$ health. Regeneration is now from $$$0$$$, which was formerly $$$k$$$, to $$$k-1$$$, instead of $$$1$$$ to $$$k$$$, which is now $$$1$$$ to $$$0$$$. For clarity, create a new array $$$b$$$ such that $$$b[i] = a[i] \% k$$$.
Now, instead of letting health values wrap around, we can just initially give each octopus a multiple of $$$k$$$ more health. For example, if $$$k=3$$$ and an octopus with initially $$$2$$$ health regenerates twice, we can pretend it initially had $$$2 + 2 \cdot 3 = 8$$$ health.
Create a new array $$$c$$$ storing these new healths. Since all healths will reach $$$0$$$, it also represents the number of boulders that will hit each octopus.
To find the minimum number of boulder throws, represent the health values with a histogram, where the heights of blocks are equal to the values of $$$c$$$:

Then, erase all vertical borders between blocks. The resulting segments each represent a boulder throw:
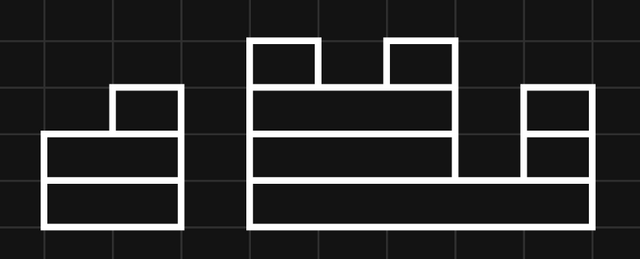
Intuitively, this should minimize the number of boulders, since any sequence of boulder throws should be rearrangeable into horizontal segments covering this histogram.
We can easily calculate the number of boulders as the sum of all positive adjacent differences, treating the far left and far right as having health $$$0$$$.

Formally, pad $$$c$$$ with an extra $$$0$$$ to the left and right (i.e. $$$c[0] = c[n+1] = 0$$$) and let the adjacent differences be $$$d[i] = c[i+1]-c[i]$$$. We claim the minimum number of boulder throws is $$$\mathrm{throws} = \sum_{i=0}^n{\max\{d[i],0\}}$$$.
This many is necessary, since if $$$d[i]$$$ is positive, octopus $$$i+1$$$ gets crushed $$$d[i]$$$ more times than octopus $$$i$$$, so at least $$$d[i]$$$ boulders' ranges have left endpoint $$$l = i+1$$$.
This many is achievable, as depicted above. Crush all octopuses with the highest health exactly once (crushing consecutive octopuses with the same boulder), then all octopuses with the new highest health, and so on. Each boulder's range's left endpoint corresponds with part of a positive adjacent difference.
Can you figure out an $$$O(n^2)$$$ solution? And can you improve on it?
Suppose you already had the optimal solution for the subarray $$$a[1 \ldots i]$$$. How could you extend it to $$$a[1 \ldots i+1]$$$?
Read the solution in Hint One before continuing with this tutorial; it provides important definitions.
To reduce the number of possibilities for each $$$c[i]$$$, we prove the following lemma: There exists an optimal choice of $$$c$$$ (minimizing $$$\mathrm{throws}$$$) where all differences between adjacent $$$c[i]$$$ have absolute value less than $$$k$$$.
Intuitively, this is because we can decrease a $$$c[i]$$$ by $$$k$$$. Formally:
We can prove this using a monovariant on the sum of all values in $$$c$$$.
Start with an optimal choice of $$$c$$$. If there does not exist an $$$i$$$ with $$$\lvert d[i]\rvert \geq k$$$, we are done.
Otherwise, choose one such $$$i$$$. Without loss of generality, we can assume $$$d[i]$$$ is positive, as the problem is symmetrical when flipped horizontally.
Now, decrease $$$c[i+1]$$$ by $$$k$$$. This decreases $$$d[i]$$$ by $$$k$$$ to a still-positive value, which decreases $$$\mathrm{throws}$$$ by $$$k$$$. This also increases $$$d[i+1]$$$ by $$$k$$$, which increases $$$\mathrm{throws}$$$ by at most $$$k$$$. Thus, $$$\mathrm{throws}$$$ does not increase, so the new $$$c$$$ is still optimal.
We can apply this operation repeatedly on any optimal solution until we do not have any more differences with absolute value $$$\geq k$$$. Since each operation decreases the sum of values in $$$c$$$ by $$$k$$$, this algorithm terminates since the sum of values in $$$c$$$ is finite.
By the previous lemma, if we have determined $$$c[i]$$$, there are at most $$$2$$$ choices for $$$c[i+1]$$$. (There is $$$1$$$ choice when $$$b[i] = b[i+1]$$$, resulting in $$$d[i] = 0$$$, $$$c[i] = c[i+1]$$$, effectively merging the two octopuses.)
We can visualize this as a DAG in the 2D plane over all points $$$(i,c[i])$$$ (over all possible choices of $$$c[i]$$$). Each point points to the points in the next column that are the closest above and below (if it exists), forming a grid-like shape. Our goal is to find a path of minimum cost from $$$(0,0)$$$ to $$$(n+1,0)$$$.
This is the DAG for the second testcase in samples: 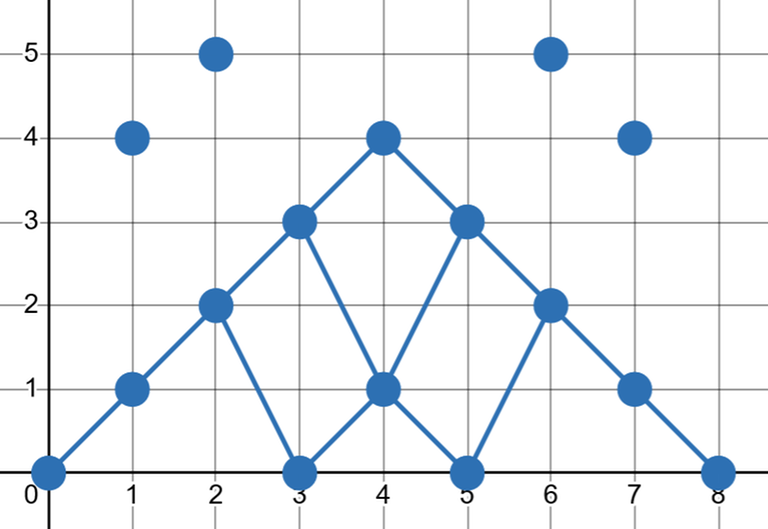
Call each time we choose a $$$c[i+1] > c[i]$$$ (i.e. positive $$$d[i]$$$) an ascent. Note that the number of ascents is fixed because each nonzero $$$d[i]$$$ is either $$$x$$$ or $$$x+k$$$ for some fixed negative $$$x$$$, and there must be a fixed number of $$$+k$$$'s to make the total change from $$$c[0]$$$ to $$$c[n+1]$$$ zero.
Each ascent brings the path up to the next "row" of descents. Since these rows slope downwards, the $$$j$$$th ascent must take place at or before some index $$$i_j$$$, because otherwise $$$c[i_j+1]$$$ would be negative.
We can use the following strategy to find a path which we claim is optimal:
If we can descend, then we descend. Otherwise, either we ascend, or alternatively, we change a previous descent into an ascent so we can descend here. (This can be further simplified by having a hypothetical "descent" here, so you do not need to compare two possibilities in the implementation.) Now, the best such location for an ascent is the one with minimum cost.
We show how to improve (or preserve the optimality of) any other path into the one chosen by this strategy. Index the ascents by the order they are chosen by the strategy, not in left-to-right order.
Let $$$j$$$ be the index of first ascent this strategy chooses that is not in the compared path. Besides the $$$j-1$$$ matching ascents, the compared path must contain at least $$$1$$$ more ascent at or before $$$i_j$$$, and because of how the strategy chooses ascents, said ascent(s) must have cost no less than the strategy’s $$$j$$$th ascent. Any can be changed to match the strategy, since the matching ascents already guarantee that each of the first $$$j-1$$$ ascents in left-to-right order happens early enough.
Repeating the above operation will obtain the strategy’s path.
We can implement the above strategy with a priority queue, where for each descent we push on the cost of the corresponding ascent, and when an ascent is required, we then pop off the minimum element. In particular, if $$$b[i] < b[i+1]$$$, then the corresponding ascent has cost $$$b[i+1]-b[i]$$$, while if $$$b[i] > b[i+1]$$$, it has cost $$$b[i+1]-b[i]+k$$$. Also, since the bottom of the DAG corresponds to $$$c[i] = b[i]$$$, an ascent is required exactly when $$$b[i] < b[i+1]$$$.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
void solve() {
int n, k;
cin >> n >> k;
priority_queue<int, vector<int>, greater<int>> differences;
int previous = 0;
ll ans = 0;
for (int i = 0; i < n; i++) {
int x;
cin >> x;
x %= k;
if (x > previous) {
differences.push(x - previous);
ans += differences.top();
differences.pop();
} else {
differences.push(k + x - previous);
}
previous = x;
}
cout << ans << "\n";
}
int main() {
int t;
cin >> t;
while (t--)
solve();
}
1852D - Miriany and Matchstick
Problem Credits: ArielShehter
Analysis: EmeraldBlock, emorgan
Solve the samples for all values of $$$k$$$.
What does constructing a second row from left to right look like?
How does knowing the possible $$$k$$$ for any first row help you construct a second row?
Apply dynamic programming to calculate the possible $$$k$$$, and use the information in the DP to construct a solution.
Call the number of adjacent pairs of cells with different characters the cost.
If we construct the second row from left to right, the amount each character adds to the cost only depends on the previous character. Thus, we can represent the problem with a DAG whose vertices represent choices for each character and whose edges represent the cost of choosing two adjacent characters. Our goal is to find a path starting from the far left and ending at the far right of cost $$$k$$$. For example, below is the DAG for the third testcase in the sample. (For convenience, we include the cost of cells in the top row with the corresponding cells in the bottom row.)

A general way to find such a path is as follows: For each vertex, store all possible costs of a path starting from the far left and ending at that vertex, which can be calculated with dynamic programming. Then we construct our path backwards from the right. For each candidate previous vertex, we check that the constructed path's cost plus the cost of the edge from this vertex plus some stored cost in this vertex equals $$$k$$$, in which case we know that some completion of the path from the far left to this vertex exists and we can choose this vertex.
Naively calculating this DP would require $$$O(n)$$$ time per operation. However, intuitively, each set of possible costs should contain almost all values between its minimum and maximum, and experiments suggest it always consists of at most two intervals. We will first formalize the DP and then prove this observation.
Let $$$\mathrm{dp}_A[i]$$$ store the set of possible values of $$$k$$$ when the grid is truncated to the first $$$i$$$ columns and the last character in the second row is $$$A$$$. Define $$$\mathrm{dp}_B[i]$$$ similarly.
Using the notation $$$[\mathrm{true}] = 1$$$, $$$[\mathrm{false}] = 0$$$, $$$S+x = \{s+x \mid s \in S\}$$$, we have the recurrences
with initial values $$$\mathrm{dp}_A[1] = [s_1 \ne A]$$$ and $$$\mathrm{dp}_B[1] = [s_1 \ne B]$$$.
Now either we hope that each set consists of $$$O(1)$$$ intervals, or we have to prove that each set indeed consists of at most two intervals:
We will use induction to prove that the following stronger property holds for all $$$i \ge 2$$$: $$$\mathrm{dp}_A[i]$$$ and $$$\mathrm{dp}_B[i]$$$ are overlapping intervals, except that possibly one (non-endpoint) value $$$v$$$ is missing from one interval, but in that case either $$$v-1$$$ or $$$v+1$$$ is present in the other interval. ($$$i = 1$$$ must be treated separately, but it can easily be checked.)
Base case. To prove this holds for $$$i = 2$$$, WLOG let $$$s_1 = A$$$ so $$$\mathrm{dp}_A[1] = \{0\}$$$ and $$$\mathrm{dp}_B[1] = \{1\}$$$. If $$$s_2 = A$$$, then
which satisfies the property with $$$v = 1$$$. If $$$s_2 = B$$$, then
which satisfies the property with $$$v = 3$$$.
Induction step. Suppose the property holds for $$$i-1$$$.
Since the conditions of the property only depend on relative positions, for convenience we shift the sets $$$\mathrm{dp}_A[i]$$$ and $$$\mathrm{dp}_B[i]$$$ left by $$$h = [s_i \ne A]+[s_i \ne s_{i-1}]$$$ to get
If the property holds for $$$\mathrm{dp}'$$$, then it holds for $$$\mathrm{dp}$$$.
First, we show that a missing value in $$$\mathrm{dp}'_A[i]$$$ or $$$\mathrm{dp}'_B[i]$$$ can only come directly from a missing value in $$$\mathrm{dp}_A[i-1]$$$ or $$$\mathrm{dp}_B[i-1]$$$ and not from the union operation merging two non-adjacent intervals. This is true because $$$\mathrm{dp}_A[i-1]$$$ and $$$\mathrm{dp}_B[i-1]$$$ overlap, so even after $$$1$$$ is added to either, they are still at least adjacent.
If a value $$$v$$$ is missing, WLOG let it be missing from $$$\mathrm{dp}_A[i-1]$$$.
If $$$v+1 \in \mathrm{dp}_B[i-1]$$$, then $$$\mathrm{dp}'_A[i]$$$ may be missing $$$v$$$ while $$$\mathrm{dp}'_B[i]$$$ does not miss any value. Also, since $$$v-1$$$ is adjacent to the missing value (which isn't an endpoint), it is in $$$\mathrm{dp}_A[i-1]$$$, so either $$$v+1$$$ or $$$v-1$$$ is in $$$\mathrm{dp}'_B[i]$$$. This also guarantees the intervals overlap, satisfying the property for $$$i$$$.
The case for $$$v-1 \in \mathrm{dp}_B[i-1]$$$ is very similar. $$$\mathrm{dp}'_B[i]$$$ may be missing either $$$v$$$ or $$$v+2$$$, and since $$$v+1 \in \mathrm{dp}_A[i-1]$$$, $$$v+1$$$ is in $$$\mathrm{dp}'_A[i]$$$.
If no value is missing, let $$$x$$$ be a common value in both $$$\mathrm{dp}_A[i-1]$$$ and $$$\mathrm{dp}_B[i-1]$$$. Then, $$$\mathrm{dp}'_A[i] \supseteq \{x,x+1\}$$$ and $$$\mathrm{dp}'_B[i]$$$ is a superset of either $$$\{x-1,x\}$$$ or $$$\{x+1,x+2\}$$$, so the intervals overlap.
To find the union of two sets of intervals, sort them by left endpoint and merge adjacent overlapping intervals. After computing the DP, apply the aforementioned backwards construction to obtain a valid second row.
Below is a visualization of solving the third testcase in the sample. Generate your own here!
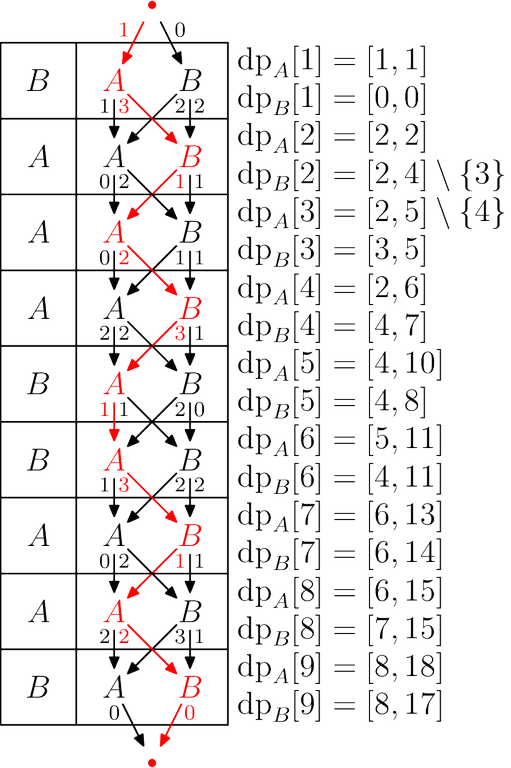
#include <bits/stdc++.h>
using namespace std;
#define all(x) (x).begin(), (x).end()
struct state {
// represents a set of integers compressed as a vector
// of non-overlapping intervals [l, r]
basic_string<array<int, 2>> a;
// add d to everything in the set
friend state add(state x, int d) {
for (auto& [l, r] : x.a)
l += d, r += d;
return x;
}
// union of two sets of integers
friend state unite(state x, state y) {
state z;
merge(all(x.a), all(y.a), back_inserter(z.a));
int j = 0;
for (int i = 1; i < z.a.size(); i++) {
if (z.a[i][0] <= z.a[j][1]+1)
z.a[j][1] = max(z.a[j][1], z.a[i][1]);
else
z.a[++j] = z.a[i];
}
z.a.erase(z.a.begin() + j + 1, z.a.end());
return z;
}
// whether integer k is in the set
friend bool contains(state x, int k) {
for (auto& [l, r] : x.a)
if (k >= l && k <= r)
return true;
return false;
}
};
// set containing only one integer d
state from_constant(int d) {
return state({{{d, d}}});
}
int main() {
ios_base::sync_with_stdio(0); cin.tie(0);
int t; cin >> t;
while (t--) {
int n, k; cin >> n >> k;
string s; cin >> s;
vector<array<state, 2>> dp(n);
dp[0][0] = from_constant(s[0] != 'A');
dp[0][1] = from_constant(s[0] != 'B');
for (int i = 1; i < n; i++) {
dp[i][0] = add(unite(dp[i-1][0], add(dp[i-1][1], 1)), (s[i] != 'A') + (s[i] != s[i-1]));
dp[i][1] = add(unite(dp[i-1][1], add(dp[i-1][0], 1)), (s[i] != 'B') + (s[i] != s[i-1]));
}
if (!(contains(dp[n-1][0], k) || contains(dp[n-1][1], k))) {
cout << "NO\n";
continue;
}
string ans;
for (int i = n-1; i >= 0; i--) {
char c = contains(dp[i][0], k - (i == n-1 ? 0 : (ans.back() != 'A'))) ? 'A' : 'B';
k -= (c != s[i]);
if (i > 0)
k -= (s[i] != s[i-1]);
if (i < n-1)
k -= (c != ans.back());
ans += c;
}
reverse(all(ans));
cout << "YES\n" << ans << "\n";
}
}
1852E - Rivalries
Problem Credits: buffering, ArielShehter, fast-fourier-transfem
Analysis: oursaco
For each distinct value, only the leftmost and rightmost positions actually have an effect on the power.
Think of each distinct value as an interval corresponding to its leftmost and rightmost positions, and let that distinct value be the value of its interval. If interval $$$x$$$ strictly contains an interval $$$y$$$ with greater value, then $$$x$$$ will not have an effect on the power and it can be discarded.
In order to not change the power, we can only add intervals that strictly contain an interval with greater value. Afterwards, if $$$i$$$ is not the endpoint of an interval, $$$b_i$$$ equals the largest value of an interval containing $$$i$$$.
There will only be at most one interval that we have to add. Assume that there are multiple intervals that we can add without changing the answer. In this case it is easy to see that its more optimal to combine the interval with smaller value into the interval with larger value. Thus, it is never optimal to add multiple intervals.
Read the hints.
We can remove all intervals that will not affect the power by iterating over them in decreasing order of value and maintain a segment tree that stores for each left endpoint of any processed intervals, the right endpoint that corresponds to it. Checking if an interval is strictly contained then becomes a range minimum query.
Assume that we know the value $$$x$$$ of the interval that we want to add. We can immediately fill the value for the interior of all intervals that correspond to a value greater than $$$x$$$. However, we also have to guarantee that $$$x$$$ is strictly contained by an interval with greater value, so we can try each interval to contain $$$x$$$. If are no unfilled indices the left or right side of the interval, then we want to replace the smallest filled on either side value with $$$x$$$. Otherwise, we can just fill in all the unfilled indices with $$$x$$$. Note that it is also possible for $$$x$$$ to not be able to be contained by any interval.
Thus, we can just try every possible $$$x$$$ in decreasing order and maintain the filled indices as we iterate. There are only at most $$$n$$$ values of $$$x$$$ to check, which is just the set of $$$a_i - 1$$$ that does not appear in $$$a$$$.
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define ff first
#define ss second
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int INF = 1e9 + 1;
void setIO() {
ios_base::sync_with_stdio(0); cin.tie(0);
}
pii seg[400005];
int n;
void build(int l = 0, int r = n - 1, int cur = 0){
seg[cur] = {INF, INF};
if(l == r) return;
int mid = (l + r)/2;
build(l, mid, cur*2 + 1);
build(mid + 1, r, cur*2 + 2);
}
void update(int x, int v, int l = 0, int r = n - 1, int cur = 0){
if(l == r){
seg[cur] = {v, l};
return;
}
int mid = (l + r)/2;
if(x <= mid) update(x, v, l, mid, cur*2 + 1);
else update(x, v, mid + 1, r, cur*2 + 2);
seg[cur] = min(seg[cur*2 + 1], seg[cur*2 + 2]);
}
pii query(int l, int r, int ul = 0, int ur = n - 1, int cur = 0){
if(l <= ul && ur <= r) return seg[cur];
if(l > r || ur < l || ul > r) return {INF, INF};
int mid = (ul + ur)/2;
return min(query(l, r, ul, mid, cur*2 + 1), query(l, r, mid + 1, ur, cur*2 + 2));
}
int main(){
setIO();
int t;
cin >> t;
for(int tt = 1; tt <= t; tt++){
cin >> n;
map<int, vector<int>> m;
int arr[n];
for(int i = 0; i < n; i++){
cin >> arr[i];
m[arr[i]].pb(i);
}
vector<int> rel; //relevant numbers
for(auto &i : m){
rel.pb(i.ff);
for(int j = 1; j < i.ss.size() - 1; j++){
arr[i.ss[j]] = 0;
}
}
reverse(rel.begin(), rel.end());
vector<int> nw;
build();
for(int i : rel){
int l = m[i].front(), r = m[i].back();
if(query(l, r).ff <= r){
arr[l] = arr[r] = 0;
} else {
update(l, r);
nw.pb(i);
}
}
swap(rel, nw);
set<int> s;
for(int i = 0; i < n; i++) if(!arr[i]) s.insert(i);
vector<int> vals; //possible target values
for(int i = rel.size() - 1; i >= 0; i--){
if(i == rel.size() - 1 || rel[i] - 1 != rel[i + 1]){
vals.pb(rel[i] - 1);
}
}
ll sum = 0, mx = 0, mxval = 0;
int lex = -1, rex = -1;
build();
for(int i = 0; i < n; i++) if(!arr[i]) update(i, -1);
reverse(vals.begin(), vals.end());
queue<pii> upd;
int ind = 0;
//try to add an interval with value i
for(int i : vals){
vector<int> nxt;
//try filling in all intervals > i
while(ind < rel.size() && rel[ind] > i){
int l = m[rel[ind]].front(), r = m[rel[ind]].back();
set<int>::iterator it = s.lower_bound(l);
while(it != s.end() && *it < r){
sum += rel[ind];
update(*it, rel[ind]);
upd.push({*it, rel[ind]});
it = s.erase(it);
}
nxt.pb(rel[ind++]);
}
//try each necessary interval to be strictly contained by i
for(int j : nxt){
int l = m[j].front(), r = m[j].back();
if(s.size() && 0 < l && r < n - 1){
//find which indeces on each side to replace with i
pii rnw = query(r + 1, n);
pii lnw = query(0, l - 1);
if(rnw.ff == INF || lnw.ff == INF) continue;
ll add = (ll)i*s.size() + (rnw.ff == -1 ? 0 : i - rnw.ff) + (lnw.ff == -1 ? 0 : i - lnw.ff);
if(i && sum + add > mx){
mx = sum + add;
mxval = i;
lex = (lnw.ff == -1 ? -1 : lnw.ss);
rex = (rnw.ff == -1 ? -1 : rnw.ss);
//it is optimal to fill in all intervals > i
while(!upd.empty()){
arr[upd.front().ff] = upd.front().ss;
upd.pop();
}
}
}
}
}
//don't want to add any intervals
if(s.size() == 0 && sum > mx){
mx = sum;
lex = rex = -1;
//it is optimal to fill in all remaining intervals
while(!upd.empty()){
arr[upd.front().ff] = upd.front().ss;
upd.pop();
}
}
if(lex != -1) arr[lex] = 0;
if(rex != -1) arr[rex] = 0;
for(int i = 0; i < n; i++) cout << (arr[i] ? arr[i] : mxval) << " ";
cout << endl;
}
}
1852F - Panda Meetups
Problem Credits: Benq
If we want to answer one of the questions (say, the question involving all the events) in polynomial time, how do we do it?
Construct a network with edges from the source to each of the red panda events with capacities equal to the number of red pandas, edges from red panda events to blue panda events with innite capacities if the red pandas can catch the corresponding blue pandas, and edges from each of the blue panda events to the sink with capacities equal to the number of blue pandas.
The next step is to use the max-flow min-cut theorem: the maximum flow is equal to the minimum number of red pandas plus blue pandas we need to remove from the graph such that no remaining red panda can reach any remaining blue panda.
How do we go from here?
For any cut, consider the region of the $$$x$$$-$$$t$$$ plane reachable by the remaining red pandas. No remaining blue pandas can lie in this region, and its border is a polyline that intersects each vertical line in the $$$x$$$-$$$t$$$ plane exactly once. Furthermore, the slope of every segment in this polyline has slope plus or minus $$$1$$$. Conversely, we can associate every polyline satisfying this condition with a cut; we just need to remove every red panda lying below the polyline and every blue panda lying on or above the polyline.
Now, figure out how to answer the queries online.
Read the hints to understand the solution better.
We can answer the queries online. For each $$$x$$$-coordinate $$$x$$$, maintain a treap that stores for every $$$x$$$-coordinate, the minimum cut $$$dp[x][t]$$$ associated with a polyline satisfying the condition above that starts at $$$x = -\infty$$$ and ends at $$$(x, t)$$$ when only considering events with $$$x$$$-coordinate at most $$$x$$$. When transitioning from to $$$x$$$ to $$$x+1$$$, we need to set for every $$$dp[x+1][t] = min(dp[x][t-1], dp[x][t], dp[x][t+1])$$$ for every $$$t$$$. To do this quickly, we maintain the values of $$$t$$$ where $$$dp[x][t+1] - dp[x][t] \neq 0$$$ in increasing order, of which there are at most $$$n$$$. When $$$x$$$ increases by one, each value of increases or decreases by one, depending on the sign of $$$dp[x][t+1]-dp[x][t]$$$, and some of the values of $$$t$$$ merge, decreasing the size of our treap. As long as we can process each merge in $$$\log n$$$ time, our solution will run in $$$O(n\log n)$$$ total time. When processing an event, we need to increase all $$$dp$$$ values in a suffix for red panda events, and all $$$dp$$$ values in a prefix for blue panda events. To answer a query, we just need to return the minimum prefix sum in our treap.
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define ff first
#define ss second
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int INF = 1e9 + 1;
void setIO() {
ios_base::sync_with_stdio(0); cin.tie(0);
}
struct node {
//mnpos - leftmost negative
//mxpos - rightmost positive
int pos, tag, mnpos, mxpos;
//minimum distance
pair<int, pii> mndif;
ll sum, pre, val;
int weight;
node(){}
node(int pos_, ll val_){
pos = pos_;
val = val_;
sum = val;
pre = min((ll)0, val);
mxpos = -INF;
mnpos = INF;
mndif = {INF, {INF, INF}};
if(val > 0) mxpos = pos;
if(val < 0) mnpos = pos;
tag = 0;
weight = rand();
}
};
int sz = 1;
node treap[1000005];
int left0[1000005];
int right0[1000005];
int newnode(int pos, ll val){
treap[sz] = node(pos, val);
return sz++;
}
pair<int, pii> comb(int a, int b){
if(a == -INF || b == INF) return {INF, {INF, INF}};
return {b - a, {a, b}};
}
void pull(int x){
treap[x].sum = treap[x].val;
treap[x].pre = min((ll)0, treap[x].val);
treap[x].mxpos = -INF;
treap[x].mnpos = INF;
treap[x].mndif = {INF, {INF, INF}};
if(treap[x].val > 0) treap[x].mxpos = treap[x].pos;
if(treap[x].val < 0) treap[x].mnpos = treap[x].pos;
if(left0[x]){
treap[x].mndif = min(treap[x].mndif, treap[left0[x]].mndif);
treap[x].mndif = min(treap[x].mndif, comb(treap[left0[x]].mxpos, treap[x].mnpos));
treap[x].mnpos = min(treap[x].mnpos, treap[left0[x]].mnpos);
treap[x].mxpos = max(treap[x].mxpos, treap[left0[x]].mxpos);
treap[x].pre = min(treap[left0[x]].pre, treap[left0[x]].sum + treap[x].pre);
treap[x].sum += treap[left0[x]].sum;
}
if(right0[x]){
treap[x].mndif = min(treap[x].mndif, treap[right0[x]].mndif);
treap[x].mndif = min(treap[x].mndif, comb(treap[x].mxpos, treap[right0[x]].mnpos));
treap[x].mnpos = min(treap[x].mnpos, treap[right0[x]].mnpos);
treap[x].mxpos = max(treap[x].mxpos, treap[right0[x]].mxpos);
treap[x].pre = min(treap[x].pre, treap[x].sum + treap[right0[x]].pre);
treap[x].sum += treap[right0[x]].sum;
}
}
int move(node& x, int shift){
int ret = x.pos;
if(x.val < 0) ret -= shift;
if(x.val > 0) ret += shift;
return ret;
}
void apply(int x, int tag){
treap[x].pos = move(treap[x], tag);
treap[x].tag += tag;
if(treap[x].mnpos != INF) treap[x].mnpos -= tag;
if(treap[x].mxpos != -INF) treap[x].mxpos += tag;
if(treap[x].mndif.ff != INF){
treap[x].mndif.ff -= 2*tag;
treap[x].mndif.ss.ff += tag;
treap[x].mndif.ss.ss -= tag;
}
}
void push(int x){
if(!treap[x].tag) return;
if(left0[x]) apply(left0[x], treap[x].tag);
if(right0[x]) apply(right0[x], treap[x].tag);
treap[x].tag = 0;
}
int merge(int a, int b){
if(!a) return b;
if(!b) return a;
if(treap[a].weight < treap[b].weight){
push(a);
right0[a] = merge(right0[a], b);
pull(a);
return a;
} else {
push(b);
left0[b] = merge(a, left0[b]);
pull(b);
return b;
}
}
//splits rt's tree into [0, k) [k, INF)
pair<int, int> split(int x, int k){
if(!x) return pair<int, int>{0, 0};
push(x);
pair<int, int> ret;
if(treap[x].pos < k){
ret = split(right0[x], k);
right0[x] = ret.first;
ret.first = x;
} else {
ret = split(left0[x], k);
left0[x] = ret.second;
ret.second = x;
}
pull(x);
return ret;
}
int rt = 0;
void erase(int x){
pair<int, int> a = split(rt, x);
pair<int, int> b = split(a.second, x + 1);
rt = merge(a.first, b.second);
}
//position, value
void insert(int a, ll b){
if(!rt){
rt = newnode(a, b);
return;
}
pair<int, int> nw = split(rt, a);
rt = merge(nw.first, merge(newnode(a, b), nw.second));
}
//value
ll query(int x){
pair<int, int> a = split(rt, x);
pair<int, int> b = split(a.second, x + 1);
ll ret = (b.first ? treap[b.first].val : 0);
rt = merge(a.first, merge(b.first, b.second));
return ret;
}
int main(){
setIO();
int n;
cin >> n;
int prv = 0;
ll st = 0;
for(int i = 1; i <= n; i++){
int x, t, c;
cin >> x >> t >> c;
int dif = x - prv;
//remove overlap
while(rt && treap[rt].mndif.ff <= 2*dif){
pair<int, pii> x = treap[rt].mndif;
ll a = query(x.ss.ff), b = query(x.ss.ss);
ll sub = min(a, -b);
erase(x.ss.ff);
erase(x.ss.ss);
a -= sub, b += sub;
if(a != 0) insert(x.ss.ff, a);
if(b != 0) insert(x.ss.ss, b);
}
//shift everything
if(rt){
treap[rt].pos = move(treap[rt], dif);
treap[rt].tag += dif;
if(treap[rt].mnpos != INF) treap[rt].mnpos -= dif;
if(treap[rt].mxpos != -INF) treap[rt].mxpos += dif;
if(treap[rt].mndif.ff != INF){
treap[rt].mndif.ff -= 2*dif;
treap[rt].mndif.ss.ff += dif;
treap[rt].mndif.ss.ss -= dif;
}
}
ll cur = query(t + 1);
if(cur != 0) erase(t + 1);
if(cur - c != 0) insert(t + 1, cur - c);
if(c > 0) st += c;
cout << st + (!rt ? 0 : treap[rt].pre) << endl;
prv = x;
}
}










One of the editorials of all time.
1: The name Ina of the Mountain was inspired by Vaan Ch.'s Ina of the Mountain series (also linked above).
2: Suisei's boulder throwing was inspired by a Holograffiti episode.
3: There were at least 9 versions of the problem statement, not including different constraints. (I forget exactly the chronology; this list is out of order to make explanation easier.) If different constraints are counted, there are probably 3-4 more, as I proposed using an $$$O(n^2)$$$ solution as a subtask; this was ultimately rejected.
It all started when I was born. Years later, I came up with a certain competitive programming problem.
The original problem was inspired by the Collatz Conjecture (more info here). Instead of boulders reducing health values by 1, except for when they regenerate to k, moves would apply the Collatz function, and the final state would be all 1s. The Collatz function has a similar cycle to the current problem, but it only has a period of 3, corresponding to $$$k=3$$$ in the version of the problem used in this round.
The second version artificially changed the period to be higher, by restricting input values to powers of two and multiplying the number by $$$2^k - 1$$$ after it reached 1.
This second version solely involved Lothar Collatz, but I decided to include Ina as well, creating the third version: "Ina Solves the Collatz Conjecture".
In short, this version went something like this:
Ninomae Ina'nis was given a problem by Lothar Collatz. Ina discovered a truly marvelous proof of this, but it was too long to fit in this problem statement.
The problem was too trivial, so she wanted to make a more complicated version. She gives you an array of powers of two and a number $$$k \ldots$$$
Ultimately, the problem was better without the addition of the Collatz function or something similar with a higher cycle period. It did not add significant difficulty to the problem, as either one would have to compute the delay of each number, or the problem would use powers of 2, which reduces immediately to the current version of the problem.
Thus, two more versions were created, 4 and 5: one with no flavortext, and one with a simple flavortext mentioning a CerealCodes member.
Then, I added my own flavortext, creating version 6: "Ina goes Bonking".
After that, I edited the flavortext again to create version 7, using the title as you know it, "Ina of the Mountain".
After that, after some complaints relating to translation, the problem statement was changed one last time to version 8, renaming nearly every instance of the word "Takodachi" to "friend", as well as reformatting other things.
Finally, in version 9, the only change was that “friend” was again renamed to “octopus”.
Additionally, I made an illustration for the problem that was ultimately rejected. It is linked here:
Image credits:
Ninomae Ina'nis for the illustration of Ninomae Ina'nis.
wavelets for the photograph of Mount Fuji.
Holograffiti animators for the animation of Suisei throwing a boulder, from which a screenshot was taken (also linked above for the inspiration of Suisei's boulder throwing).
MAZEL for the illustration of Kiryu Coco.
Myself for the drawing of the Takodachis (octopuses) and healthbars on Krita, as well as chroma-keying all the parts of and putting together the image on GIMP.
I have found a truly marvelous proof of the truth of the Collatz Conjecture, but it is too long to fit in the confines of this postscript.
such a well written editorial :heart_eyes:
also i get photo credits :OO
great contest and Very interesting problemset :) ,but HUGE skill gap between div2B and div2C
Interesting Problems and quick editorials :3
I like problems 1A 1C very much, but have not enough time for 1D...
Also, isn't 1A too difficult for this place?
yes, it was, we are sorry about that. glad you still liked it.
wow, that is fast
the hardest div 2 i have ever seen :<
I am not able to implement C on time. But this is not the hardest.
oh so which is the hardest TvT
I don't remember a lot. But, the contest(Codeforces Round 885 (Div. 2)) was hard for me. Contest of love(Vika).
oh the last div 2 TvT it shocked me a lot TvT
Try C problem from goodbye 2022,that I consider hardest C, considering binary search solution for this problem its a pretty easy problem , its a plain binary search.
Slightly sad that more people didn't find the really cool O(n) solution for C, but glad that people who solved it seemed to like it
Can you explain the $$$O(n)$$$ solution?
Additionally, my solution for D1A was $$$O(k \log n \log nk)$$$ and I can't understand the editorial of $$$O(n + k)$$$ solution, can you explain it more in details!?
I can take a stab at it! I am not sure if this is the same as the editorial, but the following submission: 215239360 has the same complexity O(n+k).
The first thing to notice is that the answer is at least the mex of the array. Therefore, we can start from the mex. If this is 1, then the answer MUST be one which should be intuitive. Otherwise, lets sort the array and try to build the answer from day 1 to day k.
Notice that with any day, the answer will increase by an amount equal to the current prefix of the array we take.
ie. Let us say we have the array [ 1 , 15 , 30 ]. The answer will increase by 1 while it is <15, then we "take" 15 and the answer will increase by 2 while it is <30, then the answer will increase by 3 for the rest of the days. Using this idea, all we have to calculate is the number of days until we can take the next element. Look at the above solution for more details :) Let me know if you have any questions.
hi, but in the example that you showed I understood that we keep on taking 1 while the answer is < 15 but how are we going to take into account the fact that the elements at the position 15 and 30 are going to be removed because If we don't take that into account and I am assuming that ans in your solution represents the current mex then when we reach 30 it is already removed similarly 31 is already removed and ...
Well, the elements that 15 and 30 affect don't matter until we take them. When taking 15, all that means is accounting for elements 15 would have deleted.
The condition that "no two elements sum to 0" implies that every bi has a distinct absolute value
Why?
For
a = [4,4,4,4],b = [ 4,4,4,4]is a valid solution.Sorry, I was reciting my thought process to come up with the intended solution. I've deleted that part now; it's not necessary to solve the problem.
I thought that too, "all absolute values are different", and it helped me to solve the problem faster. Later I realized that this mistake doesn't affect the solution
in C you have four paragraphs of absolutely obvious text then only one sentence related to the solution and it's absolutely unclear
just edited, is it clearer now
good 1a/1b/1c! I'm trying to improve my IQ for 1d.
Another way to solve Div2C is to note that the answer for $$$day=k$$$ is the $$$\text{(answer for day=k-1)^{th} }$$$ mex of the array $$$a$$$.
Overall time complexity is $$$O(n+k*\log_2(n))$$$.
can you share how did you reached to this conclusion? Non-origination
Denote $$${mex}_i$$$ to be the $$$i^{th}$$$ mex of the array $$$a$$$, i.e. the $$$i^{th}$$$ smallest positive integer that is not present in $$$a$$$. The values remaining after Day 1 are seen to be $$${mex}_1,{mex}_2,{mex}_3,{mex}_4,\ldots$$$. View this sequence as just a symbolic replacement of the values remaining initially($$$1,2,3,4,\ldots$$$). Since the algorithm of removal is the same for each day, it follows that the values remaining after Day 2 are $$$mex_{mex_1},{mex}_{{mex}_2},{mex}_{{mex}_3},{mex}_{{mex}_4},\ldots$$$. This pattern holds for the values remaining at the end of any Day by induction.
For example, consider the second sample test case. Here $$${mex}_1=2,{mex}_2=4,{mex}_3=8,{mex}_4=9,{mex}_5=10,\ldots$$$. The values remaining at the end of Day 1 are $$$2,4,8,9,10,\ldots$$$ i.e., $$${mex}_1,{mex}_2,{mex}_3,{mex}_4,{mex}_5,\ldots$$$. $$${mex}_{{mex}_1}={mex}_{2}=4,{mex}_{{mex}_2}={mex}_{4}=9,{mex}_{{mex}_3}={mex}_{8}=13,\ldots$$$. The values remaining at the end of Day 2 are indeed $$${mex}_{{mex}_1},{mex}_{{mex}_2},{mex}_{{mex}_3},\ldots$$$=$$$4,9,13,\ldots$$$.
How are you keeping track of k-1th mex of the array?
In my submission, I iteratively compute the ith mex of the array for all 1≤i≤k. You can refer to my submission https://codeforces.net/contest/1853/submission/215255944
Here $$$f(a,prefix,i)$$$ computes the ith mex of the array $$$a$$$. The jth element of the prefix array stores the number of positive integers that are not present from $$$1$$$ till the value of the jth element of the array $$$a$$$ (So $$$prefix[j]$$$ is actually just $$$a_{j}-(j+1)$$$ in 0-based indexing). You can binary search the value $$$i$$$ in this prefix array in order to calculate the ith mex of the array in $$$log2(n)$$$ time. The base case where $$$i=1$$$ is calculated beforehand and the ith mex for 2≤i≤k can be calculated by iteratively calling the function $$$f(a,prefix,\text{answer for day i-1})$$$.
I was about to become Candidate Master today but got FST (Failed System Testing) on the B problem : (
I still became Candidate Master : )
Quoting from 1852B/Solution -
That is incorrect. Two elements can still have equal absolute value (for e.g. -3 and -3). However it can proved that if a solution with two equal elements exists, then there must also be a solution having every $$$bi$$$ value distinct.
Luckily, I made the same conclusion as given in the editorial at the time of the contest, so I did not have to prove the above statement mid contest. But those who did realize it, I feel bad for you for having to prove it xD
P.S. great problem, btw!
Please, can you kindly tell me how to prove it? ty very much!
Love the editorial with hints :) Also C was hard, I solved B fast but stuck at C until the end of the contest lol.
tnx 4 fast editorial
Must problem div2C use long long? I found one of my friends passed it without using long long.
answer can be up to $$$10^{10}$$$, so yes
Oh, its so pity I cannot hack my friend...
le that friend using
#define int long longI solved Problem C with binary search. I search if we can delete a prefix of numbers 1, 2, 3, ... x using given operations. If we can delete it then we can also delete prefix upto x-1, x-2 and so on.
Can you explain it please? I am facing trouble to understand this. I worked specific number. Like I took a number and checked whether it can be the answer or not. That's why I didn't get exact answer.
Let's say if x is the answer, then we should be able to delete everything from 1, 2, ... x-1 but not x. So I search for the smallest ending prefix that we can't entirely delete using all operations and that would be our answer.
How did you check all the elements before x is deleted or not?
A recursive solution of 1853B - Fibonaccharsis:
If n equals to the k-th Fibonacci number F[k], then the answer is 1.
If n < F[k], then the answer is 0.
Otherwise, let us replace n by n-F[k]. Note that the difference of any fibonacci-like sequence and the standard fibonacci sequence is also fibonacci-like, unless the case where the first two elements of our initial sequence are equal. But this happens if and only if n is divisible by F[k+1], and this adds precisely 1 to the answer.
Code: 215213454
"...unless the case where the first two elements of our initial sequence are equal. But this happens if and only if n is divisible by F[k+1], and this adds precisely 1 to the answer."Can you PLEASE explain this a little more. I tried for a good amount of time but can't figure this out.Consider a fibonacci-like sequence S[1], S[2], S[3], S[4] ... and let us try to subtract the standard fibonacci from it. We obtain S[1], S[2]-1, S[3]-1, S[4]-2, ....
If S[1] < S[2], then this new sequence is non-decreasing, so it is also fibonacci-like.
Otherwise, we have S[1] = S[2] = c for some c. But then S[3] = 2c, S[4] = 3c, S[5] = 5c, etc. So this is the standard fibonacci sequence scaled by c and shifted by 1. That is, S[m] = cF[m+1] for all m. In particular, n = S[k] = cF[k+1]. Therefore, the case S[1] = S[2] is possible if and only if n is divisible by F[k+1], and this sequence is uniquely determined by S[1] = S[2] = n / F[n+1].
WOAHH, THAT WAS SO NEAT. THANKS A LOT AGAIN. I understand it now. This brought me so much joy. God bless you.
By, the way any comments about time complexity of this solution ?
The time complexity is O(n/F[k]). So in the worst case (for small k) it becomes O(n).
That means this works faster than the editorial's solution in the average case ?
Since the editorial's solution has complexity O(n log(n)), then, theoretically, yes.
But actually the editorial's solution 215343605 works faster, even after replacing recursion with the while loop in my solution 215343795.
Cannot understand editorial of div2C
In the editorial, I visualize the numbers in Ntarsis' set in a line arranged in increasing order; I'll make that part more clear.
Well, I couldn't solve B yet I want to know if the following observation is correct ? "if the k-th element of a real-fibonacci(starting with 0,1) is greater than the required n, then the ans has to be zero". I just don't trust myself so it would be nice if anyone could point out if this wrong ?
Yes
1852D — Miriany and Matchstick
how would ABABAABAB be a valid answer for:
9 17 BAAABBAAB since its just 13 and k is 17 ?
B A A A B B A A B | | | | | | A B A B A A B A B
thats 6
A_B_A_B_A.A_B_A_B
and thats 7
what I miss ?
you didn't count the adjacencies in the top row of the matchstick
I hate the fact that it's so relatable.
div1D can also be solved using greedy, because most of the time, each operation only adds one to the answer.
Here's my code: https://codeforces.net/contest/1852/submission/215259895
Very nice. Our original solution was greedy, but it got RTE after we prepared the problem.
It can also be solved through random algorithm, we can determine the answer from back to front and choose the answer which is legal randomly. Here's my code:https://codeforces.net/contest/1852/submission/215263597
I used a mysterious method to pass this problem in C of Div2, with time complexity O(n). Is anyone interested in proving the right thing to do? https://codeforces.net/contest/1853/submission/215254923
Was somebody able to AC div1D with divide and conquer + fft/ntt in O(nlog^2n)? My code ACs in around 15s, which is not close to the TL, but maybe it's possible to squeeze it in the TL with a faster fft/ntt implementation
I am, but only after contest. Link
It demanded a lot of constant optimizations — like making simultaneously fft and inverse fft for two polynomials at once (described here in p.16) and using
floatas data type for complex numbers.Thanks for sharing, I'll definitely take a look at those optimizations
I saw many solving C with binary search, can anyone explain it?
I solved Div2 C by binary searching on the minimum length $$$\ell$$$ of the set $$$A_\ell = [1, \ldots, \ell]$$$ such that performing the operations on the (finite-size) array $$$A_\ell$$$ left the set nonempty after $$$k$$$ steps. Observe that if $$$A_\ell$$$ is empty after $$$k$$$ operations but $$$A_{\ell+1}$$$ is not, then $$$\ell+1$$$ is our answer. For a given $$$\ell$$$ my solution determined the smallest $$$k'$$$ such that $$$A_\ell$$$ is empty after performing $$$k'$$$ steps, and compares $$$k'$$$ to $$$k$$$ to update the search bounds.
To simulate the procedure for a given $$$\ell$$$, notice that up to relabeling, all that really matters at each step is the number of elements $$$x$$$ remaining in the set. This allows us to simulate the deletion in $$$O(n)$$$ regardless of $$$\ell$$$ by repeatedly (1) updating the number of elements $$$m$$$ that will be removed (i.e., the maximal $$$m$$$ such that $$$a_m <= x$$$) and (2) performing the maximum number of steps removing that many elements in $$$O(1)$$$.
The answer is upper bounded by $$$nk + 1$$$. The total runtime is thus $$$O(n \log (nk)) = O(n \log n + n \log k)$$$.
Submission: 215276044
My binary search is similar. I do binary search on the answer (that is $$$l+1$$$, but call it $$$ans$$$), and check if it is deleted from $$$a_n$$$ to $$$a_1$$$.
Suppose the number deleted by $$$a_i$$$ in the $$$j$$$-th round is $$$x$$$. Since in this round i numbers $$$\le x$$$ are deleted, the number deleted by $$$a_i$$$ in the $$$(j+1)$$$-th round should be the $$$i$$$-th undeleted number after $$$x$$$. The numbers deleted this time which are greater than $$$x$$$ must be deleted by $$$a_{l>i}$$$, so do it from $$$a_n$$$ to $$$a_1$$$.
Suppose $$$y$$$ numbers smaller than $$$ans+1$$$ are deleted by $$$a_{n},a_{n-1},\dots,a_{i+1}$$$, there're now $$$ans-a_i+1-y$$$ numbers not deleted in $$$[a_i,x]$$$. Since it goes $$$i$$$ steps each time, the answer for $$$a_i$$$ is $$$\lceil\frac{ans-a_i+1-y}i\rceil$$$.
Just sum them up and check if the value is $$$\le ans-1$$$. If so, the real answer should be less or equal to the current. The time complexity is $$$O(n\log \text{ANS})$$$
Thank you so much! Finally understood.
pls can you explain DIV 2 D , I was unable to understand from editorial
esr6vqa LMydd0225 thanks to you both, I got the intuition and how we could come up with such solution,thanks again.
Bonus solution of D2B can be optimized up to O(1) per testcase (with the precalc of Fibonacci numbers) knowing that
can someone explain how to reach this equation?
Assume that we've proven
.
Thus
We can close the brackets and see that
Which means that
Thanks a lot!
This div2C is where I doubted my entire existence :( --> cries in low IQ
Is it just me or C was harder than D?
In problem D(Div2),can someone please explain the Hint1 given in the editorial(I mean why is this statement true).
Let's say you have 2 ones in $$$b$$$. Then you didn't use at least one number from $$$1$$$ to $$$n$$$ as the absolute value. You can add 1 to all numbers, which absolute values are less than that missing number, then you won't have $$$2$$$. Then you can replace one of ones with two and all constraints will still be true.
Another solution for Div $$$2$$$ B.
We can write $$$f_k$$$ as a linear combinaison of $$$f_1$$$ and $$$f_2$$$. Thus by precomputing these coefficient for $$$k \le 30$$$. Let $$$f_k = a \cdot f_1 + b \cdot f_2$$$ the problem is reduced to finding $$$f_1$$$ and $$$f_2$$$ for which $$$f_k = n$$$. now knowing that $$$f_1 \le f_k$$$ since $$$(f)_n$$$ is increasing we can try all $$$0 \le f_1 \le n$$$. Since $$$a, b, f_k$$$ are fixed we can check if there is $$$f_2$$$ verifying the aforementioned conditions. Submission
The explanation for div1D is kinda bad. "we can show that [...]" isn't sufficient, please show it. It took me a long time to realize that when you flip b2...bn-3, then the thing changes by some odd value.
Hi, we are already in the process of rewriting the editorial for this problem. Please wait a bit and check back :)
A little late, but I wanted to share my solution for div2C/div1A that runs in $$$O(k \log n \log a_i)$$$ time.
Consider binary searching on the answer. To check if a certain $$$mid$$$ is valid, we have to determine if all the values $$$\leq mid$$$ will end up getting deleted over the course of the $$$k$$$ days. To determine the number of values $$$\leq x$$$ which get deleted for some $$$x$$$, we just have to find the number of values in $$$a$$$ that are $$$\leq x$$$. This can be done with a second binary search or builtin functions like
std::upper_bound. After determine the amount that are deleted, we can subtract this from $$$mid$$$ and simulate the remaining days on the new $$$mid$$$. This gives an $$$O(k \log n$$$ check function and an $$$O(k \log n \log a_i)$$$ sol overall.Code:
This is basically what I did; the inner check can additionally be done in $$$O(n)$$$ by maintaining a pointer to the amount $$$m$$$ subtracted off (it can only decrease) and additionally subtracting off as many multiples as possible in a single step. In my code this looks like
This nicely allows larger constraints on $$$k$$$.
i love cerealcodes <3
Great round! but the statement of 1852D is a little unfriendly to people suffer from red-blindness like me, it will be better if you show "the pairs of different characters" in bold rather than in red.
Tough round. Yes, I cry.
Good round! I love the ideas, very stimulating. Here's another solution for D1B/D2D, using hashing.
Firstly sort $$$a$$$, then $$$b$$$ becomes a increasing sequence. Try to find a $$$pos\in [0,n]$$$ satisfies that $$$b_{pos}<0$$$ and $$$b_{pos+1}>0$$$ (we assume that $$$b_0=-\infty$$$ and $$$b_{n+1}=+\infty$$$). Notice that for a $$$b_i<0$$$,it will exactly match up with $$$[n,n-a_i+1]$$$. and for a $$$b_i>0$$$, it match up with $$$[pos+1,n]$$$ in addition. Now we say there's a solution, if and only if there's a $$$pos$$$ that satisfies every index $$$i$$$ have been matched exactly $$$a_i$$$ times.
Now let's construct a solution to prove it. Assume that $$$b_{pos},b_{pos+1},…,b_{n}$$$ equals to $$$1,2,…,n-pos$$$ at the beginning. For every $$$b_i<0$$$, we let $$$b_i=b_{n-a_i+1}$$$, and add $$$1$$$ to all the $$$b_j(j\not =i)$$$ that are equal or greater than it. In the end it will generate a correct $$$b$$$. We can use a difference array to make it in $$$O(n)$$$.
Then the problem is how to find a $$$pos$$$. Check every possible value. Process the hash value of sequences like $$$1111…1$$$, then you can check each value in $$$O(1)$$$.
The total time complexity is $$$O(n\log n)$$$ due to sorting.
In div1C, I try to use dp to solve it but failed. let dp[i][j] be the min operations that position i is decreased by a[i]+j*k times and dp[i][j]=min dp[i-1][j']+max(0,a[i]+j*k-a[i-1]-j'*k) I don't know if there are anywhere wrong.
It's been a day but I still don't understand what is the (a[inc] — ans + inc — 1) in the problem Ntarsis' Set :-(
Check out the other solution here; the model has lower readability, it's there to showcase an $$$O(n)$$$ solution.
$$$\lfloor \frac{a[inc]-ans+inc-1}{inc} \rfloor \equiv \lceil \frac{a[inc]-ans}{inc} \rceil$$$ is the number of days before $$$a[inc]$$$ becomes active, until then $$$inc$$$ numbers are inserted each day in the region of interest.
thanks for information
can someone explain how they solved B(1853B — Fibonaccharsis) by using binary search....
you get the equation , now we need to find the number of solution to this equation , now you can find any one solution which satisfies the equation , now you can get the parametric coordinates for the soln of the equation , now you have to find the answer only when y is greater than x , this can be done using binary search.
parametric coordinates (x0 , y0) for the soln will be ,
let p , q be any solutions for the equation. let a , b be the coefficients of x and y
x0 = p + K * b / gcd(a , b)
y0 = q — K * a / gcd(a , b)
binary search on value of k
I don't understand your approach. Can you elaborate more?
code
I remember that this div1A appeared as the last problem in some div1 contest but with many queries asking for the number at position P at time T. Anyone that upsolved that one can link it here?
I can not understand jiangly's 1A.
Hi, I was just curious what does "Analysis" in editorial mean. Is it preparation of testcases or finding the solution to the problem and proving it or maybe converting idea into problem statement.
they’re the editorial writers for that problem
In editorial for div1C "Our goal is to find a path of minimum cost from (0,0) to (k+1,0)", shouldn't it be (n+1,0) ?
thanks, it has been fixed
samples are really great
link to problem: https://codeforces.net/contest/1853/problem/B
I have come up with an O(n*log(n)*k) solution where I loop through all possible f1, then binary search on f2. I confirm the f1 and f2 combo works through a memoized Fibonacci dp, that runs in O(k) where k denotes the kth term. But when I run it, my program times out.
Can someone help me identify what is taking my solution so long? (implementation or strategy)
I submitted it so you can view my solution: https://codeforces.net/contest/1853/submission/216182584
If you hate java like me, here is the c++ version: https://codeforces.net/contest/1853/submission/216183198
Thank you in advance
O(nk log n) will not pass under the constraints
In Problem — D — Codeforces,dose the dp only consist two intervals which are adjacent
I found a interesting solution for problem B in O(number of fibonacci numbers under n)
On the surface, it looks like you have put a lot of effort in writing the editorial. But for someone, who was not able to solve a problem, to be able to read what you have written, understand it and solve it on their own is simply not possible.
Div1A is definitely a perfect problem for learning,i spend half day try to know this and i just realize that this is a josephus problem!You can use a wishful thinking to found the formula,for example,In the first round there is 1st element,2nd element,.. and so on,and the fact is in the second round we also have 1st element,2nd element,....we don't care the value what it's we only care the position,now we need to build the connection between 2nd array to the 1st array,for example the element in 2nd array in position 1st + something like j is equal to the i-th element in 1st array if you can build this relation you will found that you can build 3nd array(3nd operation) with 2nd array and so on until k-th array with (k-1)-th array.