Problem Link: Uva 11235 — Frequent values
My Solution: Pastebin
What to do: You will be given an sorted array A of size N, where 1 <= N <= 10^5 and -10^5 <= A[i] <= 10^5. You need to determine the most frequent value of A[i] within a given range, i.e., L <= i <= R.
How to do it: We can use classical segment trees to solve this problem. We can build the tree, and then query the tree to obtain the desired answer. The main challenge lies in merging two nodes while building and performing a query. As the array is sorted in descending order, that means the values of leftNode and rightNode will always be sorted. So, We can track five things for each node: the leftMost value, the rightMost value, the frequency of the leftMost value i.e. frLeftMost, the frequency of the rightMost value i.e. frRightMost, and the ans. The Node will look like:
struct Node
{
int leftMost, rightMost, frLeftMost, frRightMost, ans;
Node() {}
};
How to merge: Assume that the current node is cur, left node is leftNode and right node is rightNode. Then, the leftMost value and rightMost value of cur node will be always -
cur.leftMost = leftNode.leftMost;
cur.rightMost = rightNode.rightMost;
The initial tree of the sample test case would look like this — 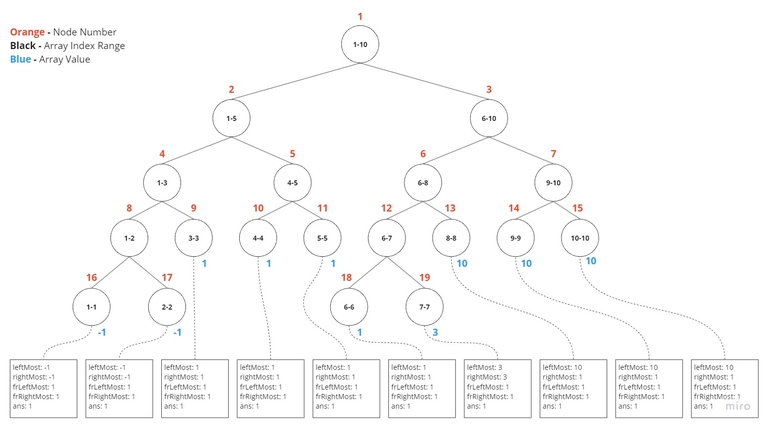
We have 5 cases now -
Case 1:
leftNode = [1,1,1] and rightNode = [1,1,1,1] — As the leftNode's leftMost value equals the rightNode's rightMost value, this implies that both of these nodes share the same value. Therefore, this frequency will serve as the answer for the current node. Additionally, the frequency of the leftMost and rightMost values of the current node will be the sum of the frequencies of the leftMost value of both the left and right nodes.
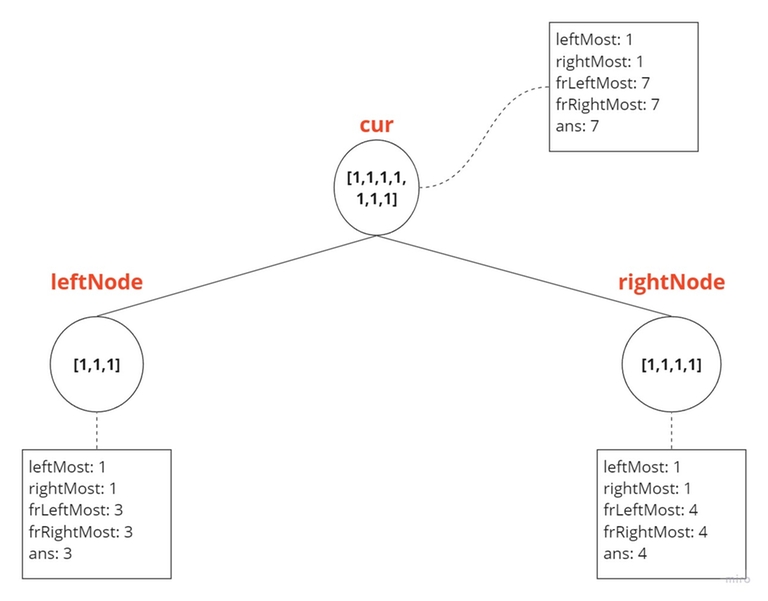
int tmp = leftNode.frLeftMost + rightNode.frLeftMost;
cur.frLeftMost = tmp;
cur.frRightMost = tmp;
cur.ans = tmp;
Case 2:
leftNode = [1,1,1] and rightNode = [1,1,2,3] — As the leftNode's leftMost equals the rightNode's leftMost, this indicates that the leftNode has all the same values, and the rightNode has some of them. Therefore, the answer for the current node will be the maximum of (leftNode.frLeftMost + rightNode.frLeftMost) and rightNode.ans. Additionally, the frequency of the leftMost value of the current node will be the sum of leftNode.frLeftMost and rightNode.frLeftMost. The frequency of the rightMost value of the current node will remain the same as the rightNode's.
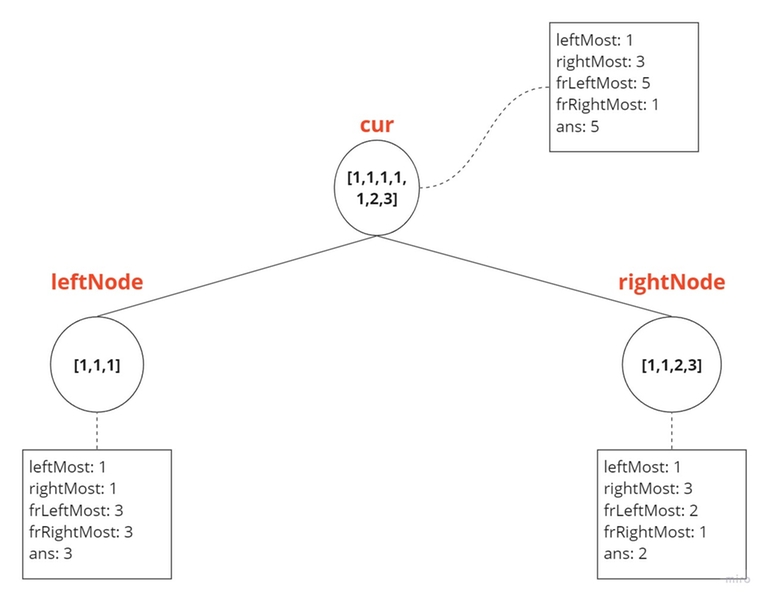
cur.frLeftMost = leftNode.frLeftMost + rightNode.frLeftMost;
cur.frRightMost = rightNode.frRightMost;
cur.ans = max(cur.frLeftMost, rightNode.ans);
Case 3:
leftNode = [1,1,2,2] and rightNode = [2,2,2] — As the leftNode's rightMost equals the rightNode's rightMost, this indicates that the rightNode has all the same values, and the leftNode has some of them. Therefore, the answer for the current node will be the maximum of (leftNode.frRightMost + rightNode.frLeftMost) and leftNode.ans. Additionally, the frequency of the rightMost value of the current node will be the sum of leftNode.frRightMost and rightNode.frLeftMost. The frequency of the leftMost value of the current node will remain the same as the leftNode's.
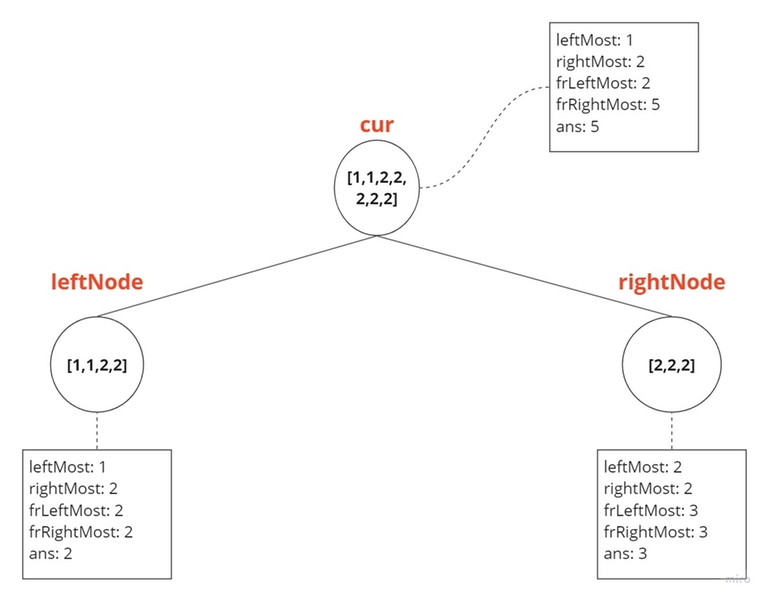
cur.frLeftMost = leftNode.frLeftMost;
cur.frRightMost = leftNode.frRightMost + rightNode.frLeftMost;
cur.ans = max(cur.frRightMost, leftNode.ans);
Case 4:
leftNode = [1,1,2,2] and rightNode = [2,2,3,4] — As the leftNode's rightMost equals the rightNode's leftMost, this means that the frequency of the leftMost value and the rightMost value of the current node won't change, and neither will the leftMost and rightMost values. However, it's possible that the answer lies in the sum of the frequency of leftNode's rightMost value and rightNode's leftMost value. Therefore, the answer of the current node will be the maximum of (leftNode.ans, rightNode.ans, leftNode.frRightMost + rightNode.frLeftMost).
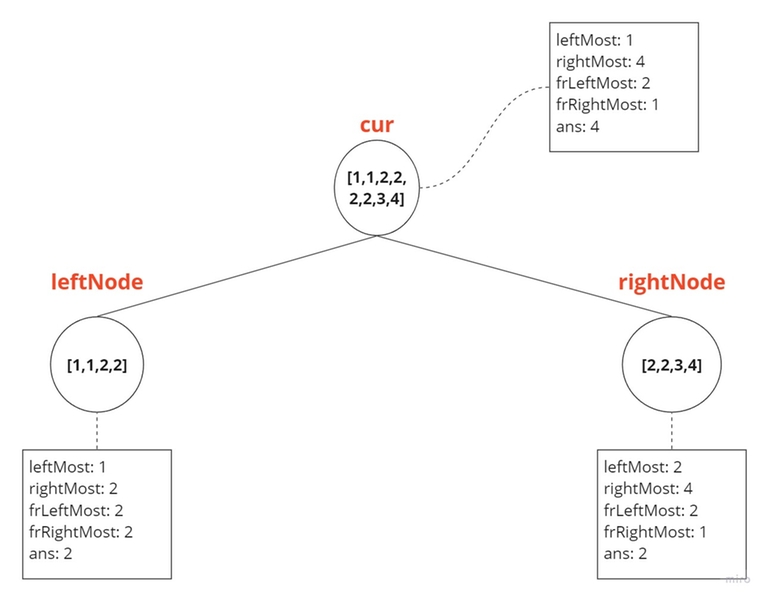
cur.frLeftMost = leftNode.frLeftMost;
cur.frRightMost = rightNode.frRightMost;
cur.ans = max({leftNode.ans, rightNode.ans, leftNode.frRightMost + rightNode.frLeftMost});
Case 5:
leftNode = [1,1,2,2] and rightNode = [3,4,5] — If none of the above cases matches, it means that the leftMost, frLeftMost, rightMost, and frRightMost values of the current node won't change. The answer will be the maximum of (leftNode.ans, rightNode.ans).
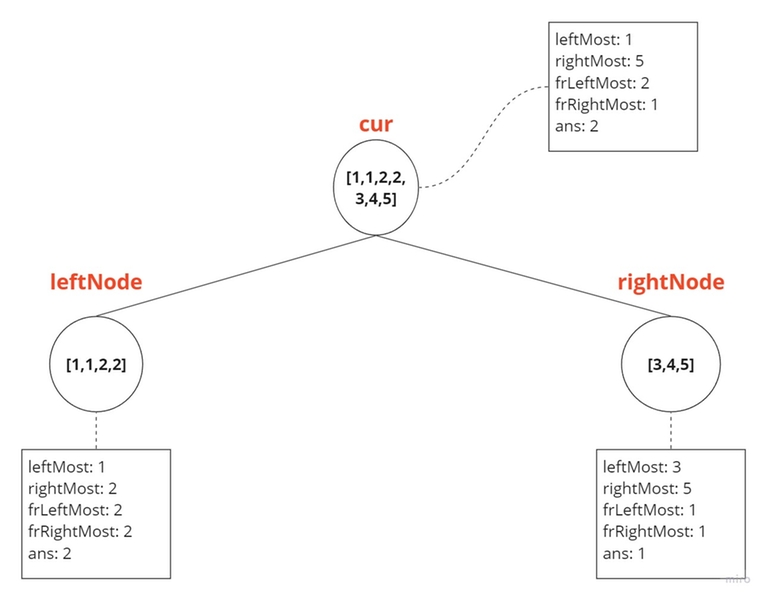
cur.frLeftMost = leftNode.frLeftMost;
cur.frRightMost = rightNode.frRightMost;
cur.ans = max(leftNode.ans, rightNode.ans);
The rest of the work will proceed as usual.











You can solve this problem easily using Mo's algo (sqrt decomposition). Sort the queries by blocks, and use a set to determine the max element that has the highest frequency in the range [L,R].
The complexity will be obviously way higher than segment tree, but i guess it's sufficient to pass the constraints in that problem (since n<=1e5 and q<=1e5), the complexity will be $$$O(n*\sqrt{n}*\log _2n)$$$
easily understandable. Thanks for the write up^^
He is the best teacher in Bangladesh.