Question:
You have a $$$N * M$$$ matrix. The color of cell in $$$i^{th}$$$ row and $$$j^{th}$$$ column is $$$a_{ij}$$$. Find the number of submatrices (rectangles that can be formed by considering a range of continuous rows and columns), that have all cells of same color.
Idea:
Let $$$i_l, j_l$$$ be the coordinates of the top left corner and $$$i_r, j_r$$$ be the coordinates of the bottom right corner. We can see that $$$(i_l, j_l, i_r, j_r)$$$ uniquely define a rectangle.
Let's call a rectangle valid if it has all cells of same color.
Now let $$$dp[i][j]$$$ be the number of valid rectangles with their bottom right corner at $$$(i, j)$$$.
Let $$$h[i][j]$$$ be the "height" of columns at $$$(i, j)$$$. That is
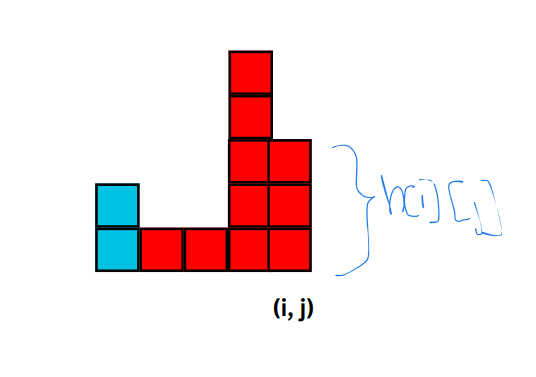
$$$h[i][j]$$$ = max value of $$$len$$$ such that $$$a[i][j] = a[i][t]$$$ , for all $$$t = i - len + 1, i - len + 2, ..., i$$$.
How do we computer $$$dp[i][j]$$$ efficiently ?
Consider how $$$dp[i][j]$$$ depends on $$$dp[i-1][j], dp[i - 2][j], ...$$$.
For some $$$k, k < j$$$, if $$$a[i][k] != a[i][j]$$$, then $$$dp[i][k]$$$ will make no contribution to $$$dp[i][j]$$$. So let's assume that $$$a[i][t] = a[i][j]$$$ for all $$$t = k, k + 1, ..., j$$$.
Now what is the maximum height of rectangle with bottom right corner at $$$(i, j)$$$ and top left corner in the column $$$k$$$ ?
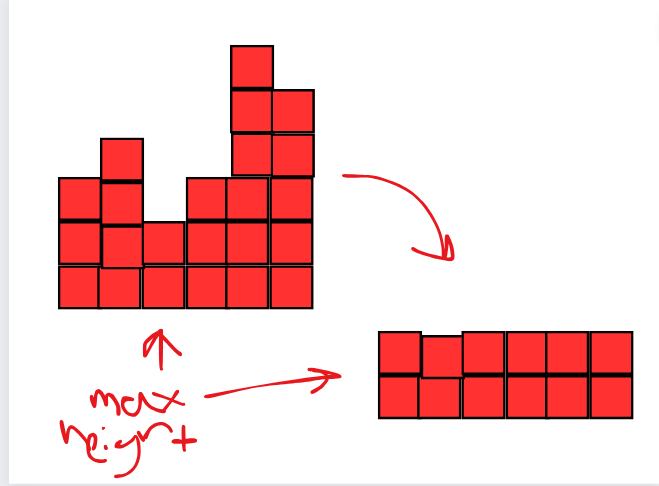
It is $$$height_k = min_{k \le t \le i}(h[i][t])$$$. Then then the number of such rectangles is $$$height_k$$$, since we can have rectangles of height $$$1, 2, 3, ..., height_k$$$.
Also consider that if $$$h[i][k] \le height_k$$$, then for any rectangle with bottom right corner at $$$(i, k)$$$ can be extended so that it has bottom right corner at $$$(i, j)$$$.
Let $$$k$$$ be the first index such that $$$a[i][k] = a[i][j]$$$ and $$$h[i][k] < h[i][j]$$$.
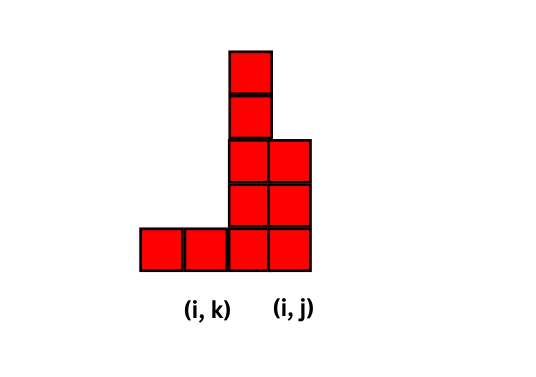
Then every rectangle with bottom right corner at $$$(i, k)$$$ can be extended to $$$(i, j)$$$. Also the height of any rectangle with top-left corner after $$$(i, k)$$$ is at most $$$h[i][j]$$$, since by definition for any $$$t, k < t \le i$$$ we have $$$h[i][t] \ge h[i][j]$$$.
Thus the number of rectangles after k are $$$h[i][j] * (j - k)$$$.
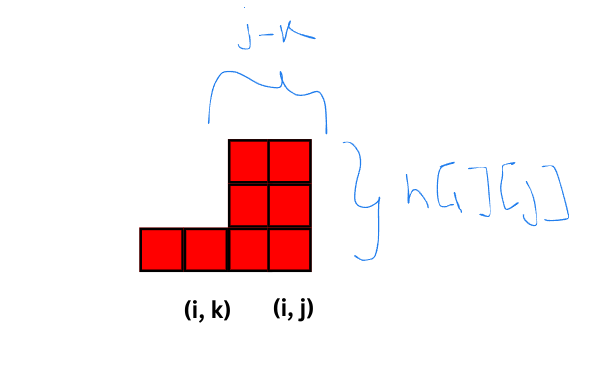
Thus we have, $$$dp[i][j] = dp[i][k] + h[i][j] * (j - k)$$$.
Now the question is how do we efficiently find $$$k$$$ ?
We can do this by maintaining an array of indices $$$col$$$ such that $$$h[i][col] \lt min_{col \le t \le j}(h[i][t])$$$.
Time Complexity : $$$O(N * M)$$$
vector<vector<ll>> get_number_of_rectangles(vector<vector<int>> &a, int n, int m){
vector<vector<ll>> dp(n, vector<ll>(m));
vector<vector<ll>> h(n, vector<ll>(m, 1));
for(int i = 1; i < n; ++i){
for(int j = 0; j < m; ++j){
if(a[i - 1][j] == a[i][j]){
h[i][j] += h[i - 1][j];
}
}
}
for(int i = 0; i < n; ++i){
vector<int> indices;
for(int j = 0; j < m; ++j){
int k = -1;
while(!indices.empty()){
int col = indices.back();
if((a[i][col] != a[i][j]) || (h[i][col] < h[i][j])){
break;
}
indices.pop_back();
}
if(!indices.empty()){
k = indices.back();
}
dp[i][j] += h[i][j] * (j - k);
if(k != -1){
if(a[i][k] == a[i][j]){
dp[i][j] += dp[i][k];
}
}
indices.push_back(j);
}
}
return dp;
}
void solve() {
int n, m;
cin >> n >> m;
vector<vector<int>> a(n, vector<int>(m));
for(int i = 0; i < n; ++i){
for(int j = 0; j < m; ++j){
cin >> a[i][j];
}
}
vector<vector<ll>> dp = get_number_of_rectangles(a, n, m);
ll ans = 0;
for(int i = 0; i < n; ++i){
for(int j = 0; j < m; ++j){
ans += dp[i][j];
}
}
cout << ans << '\n';
}










Auto comment: topic has been updated by one_autum_leaf (previous revision, new revision, compare).
This can also be solved in $$$\mathcal{O}(nm)$$$ with a method similar to CSES — Maximum Building II by enumerating the row of the bottom edge of the submatrix and using stacks to count the number of submatricies.
Can you clarify the statement? Do you mean rectangles or do you really mean matrices that can be formed by deleting some rows and columns?
The result with the first interpretation is 12, but using the second interpretation it's 19 I think (for example, you can form a matrix full of As by deleting the 2nd row and the 2nd column).
Sorry for the confusion. I meant rectangles that can be formed by considering a continuous range of columns and rows. Basically submatrices.
Auto comment: topic has been updated by one_autum_leaf (previous revision, new revision, compare).