Given n numbers a[1] to a[n], 2 player play a game alternately as follows. In the beginning of game, we have a number g = 0. They chose one of the numbers in the array a which is not thrown out and replace g by gcd(g, a[i]). After that they throw a[i]. If at any time in the game g becomes 1, the person who made the value g of equal to 1 loses. If a person is not able to move, then also he loses.
There are two questions to answer. 1. Who will win if they play optimally. 2. What is probability of winning of first player if they play randomly.
I'd like to share my solution to part 2 which is different from the editorial.
Any game they play is a permutation of a (let them play all n numbers, even someone already lose). Let's call this permutation b. Since they play uniformly randomly, the permutation is also chosen uniformly randomly from all n! permutations.
Let 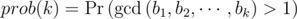 for 1 ≤ k ≤ n.
for 1 ≤ k ≤ n.
If the game ends exactly on the k th turn, that means  , but
, but  . Therefore the probability is prob(k - 1) - prob(k). If prob(n + 1) is defined as 0, then k = n + 1 is also applied. Sereja wins if and only if the game ends on even number turns, so the answer is (prob(1) - prob(2)) + (prob(3) - prob(4)) + ....
. Therefore the probability is prob(k - 1) - prob(k). If prob(n + 1) is defined as 0, then k = n + 1 is also applied. Sereja wins if and only if the game ends on even number turns, so the answer is (prob(1) - prob(2)) + (prob(3) - prob(4)) + ....
All that's left is calculate prob(k). Let 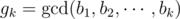 , we can calculate separately the probability that gk is a multiple of p, where p is a prime, and add them up. By the inclusion-exclusion principle, we also have to subtract the probability that gk is a multiple of p1 p2, where p1 and p2 are primes, and add back the probability that gk is a multiple of p1 p2 p3, where p1, p2 and p3 are primes. Fortunately, there is no number under 100 having 4 different prime factors.
, we can calculate separately the probability that gk is a multiple of p, where p is a prime, and add them up. By the inclusion-exclusion principle, we also have to subtract the probability that gk is a multiple of p1 p2, where p1 and p2 are primes, and add back the probability that gk is a multiple of p1 p2 p3, where p1, p2 and p3 are primes. Fortunately, there is no number under 100 having 4 different prime factors.
Finally, let's calculate the probability that gk is a multiple of m. Say there are c numbers in a that are multiples of m. Note that b1, b2, ..., bk must all be multiples of m, so all chosen from these c numbers. The number of combinations is 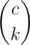 and the number of permutations is
and the number of permutations is  . So the probability is
. So the probability is 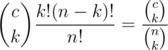 .
.
My solution: http://www.codechef.com/viewsolution/3906540











Can you explain the prob(k-1) — prob(k) part please?
Let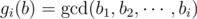 becomes 1 exactly when i = k. Then gk - 1 > 1 and gk = 1, so we subtract those cases where gk is still greater than 1 from prob(k - 1).
becomes 1 exactly when i = k. Then gk - 1 > 1 and gk = 1, so we subtract those cases where gk is still greater than 1 from prob(k - 1).
Ok, I got it! Thanks.
You're welcome :)