lperovskaya's blog

Yandex.Algorithm 2014 Elimination stage: round 3
By lperovskaya, 10 years ago, translation, In English

Today, on June 15 at 1 p.m. MSK the last round of Yandex.Algorithm elimination stage will begin. Crucial for determination of Yandex.Algorithm finalists 718 score points will be distributed during these 100 minutes. Three prize-winners of Yandex.Algorithm 2013 have already reserved a place in the final round. Have you?

  • Vote: I like it
  • +67
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Oh, NO!! I get the 26th place. :(

The task C is too evil, I misunderstand the task (ask pair of i, j s.t. abs(x[i]-x[j]) = d) but can pass all examples.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +16 Vote: I do not like it

    26th place isn't so bad: if someone declines onsite invitation, you'll be invited instead (if I understand correctly).

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      I don't know if they have such rule. At least in last year all top-25 attend the finals.

      And if it's very late to happen, then I don't have time to apply visa. Maybe you will attend instead, because you don't need a visa. :)

      → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Some of my predict come to truth: I did get the invitation, but I can't get obtain the visa in time. Unfortunately it is to late to invite you instead. :(

      → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I first thought of reducing it in such a way, but then I realized it doesn't work that way so simply :D

    Sometimes, many successful solution and passed samples can be deceiving. It happens to me quite often in TC, since they sometimes don't have maximal samples or have too weak ones. Once, I even passed the samples with a solution that had several serious mistakes in one formula... I guess they cancelled each other out or something :D

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +16 Vote: I do not like it

      Yes, but I think at least the examples should check if you read the statement correctly.

      It feels like something similar to last SRM (mod 1e9+9).

      → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I have "I64d or lld" issue!(I thought that was the same as Codeforces).

My blind A gets WA. My open C gets 4 WA before OK (after the 4th WA I turn to solve E first. Then C gets OK).

That's not a good experience for me. Hope next time there can be some clarification about that. :D

→ Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

How to solve problem F? Got TLE using SG.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +24 Vote: I do not like it

    For L<20 I use SG. For L>=20 I use the following:

    if(N == L * 2 + L - 1) return true;
if(N == L * 4 + L - 1) return true;
if(N == L * 8 + L - 3) return true;
if(N == L * 12 + L - 5) return true;
if(N == L * 16 + L - 5) return true;
if(N == L * 20 + L - 7) return true;
if(N == L * 20 + L - 7) return true;
if(N == L * 28 + L - 9) return true;
if(N == L * 32 + L - 11) return true;
if(N == L * 40 + L - 11) return true;
if(N == L * 48 + L - 13) return true;
if(N == L * 64 + L - 19) return true;
if(N == L * 68 + L - 19) return true;
return false;

    and the formulae were derived by running SG for each L and noticing the rules.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +9 Vote: I do not like it

      Apparently the next N is 397*L-121, this works for N >= 14 and is over 7000 for N >= 18. I have some intuitions why this would work, but I have not really proven anything.

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it +9 Vote: I do not like it

        Of course I meant L >= 18 and L >= 14.

        → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it +8 Vote: I do not like it

        Please, give some intuitions why this work. :) How you get this formulas?

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it +1 Vote: I do not like it

          Probably observed from running the bruteforces. We can obviously see that if 2|(N - L) or N - L <  = 2(L - 1), then it's possible to split the game into 2 identical ones or 2 instalosses in the first move; SG works fast for N up to about 1000 and decently fast (not good enough for a submit, but good enough for observing the rules) for N up to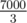 , so it's just a question of observing some rules for the remaining L (and these are large, so there are likely many winning strategies, if any).

          → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Xellos is right, from running the bruteforce. If you fix L, you can find all N such that the second player wins in O(N*L) time. This can be done for all values of L in reasonable time, and you can list all such pairs (L,N) and look for rules. There are not many such pairs (usually F wins) so it is quite easy to see that 3L-1, 5L-1, ... are S-wins, which can be confirmed by asking the program to write L in this form. Low values of L are irregular, so just solve them with SG.

          As for intuitions: assume that L is big enough. For N=L the first player wins. The same happens for N up to 3L-2 by playing in the middle, but at N=3L-1 this no longer works, and the second player wins. At 3L the first player wins again by playing the middle, which works until 5L-1, where apparently something happens again (I have not analyzed it). And so on.

          → Reply
»
10 years ago, # |
  Vote: I like it +24 Vote: I do not like it

In Gym: 2014 Yandex.Algorithm - Elimination Stage, Online Round 3.

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How can I solve problem E?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    Calculate centroid of tetrahedron and consider its projection to the surface z=0: 1) If it lies outside of triangle formed by the first 3 coordinates, then the answer is 'Falling'; 2) if it lies on the edge of triangle, then the answer is 'Unstable'. 3) if it lies strictly inside of triangle, then the answer is 'Standing'

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Ok. thanks! But how can i calculate centroid of tetrahedron?

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        You just google for the formula:

        Similarly for other coordinates.

        → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        The funny thing is that this centroid is the same for a filled tetrahedron and for unit masses in ints vertices.

        You can split the tetrahedron into many thin homothetic triangles parallel to any face; their centers of mass lie on 1 line, so the tetrahedron's will lie on it too. And you can show that a filled triangle's center of mass is the same as that of one with unit masses in its vertices, in the same way by splitting it into thin rods.

        → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How was problem A to be solved? The one in which we had to count the number of pairs of nodes at a distance 2 from each other?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Notice that the graph is a tree. It's obvious that there are no triangles, so we're counting paths of length 2. Fix a central vertex of that path, then all pairs of its (distict) neighbours are endpoints of one such path. Alltogether, there are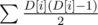 , where D[i] are degrees of vertices.

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Is there any news about T-shirts?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    I got a mail from lperovskaya yesterday, asking me to complete/check my address and T-shirt size.

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Is there any other way to solve problem B other than matrix exponentiation?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    Lol, yes

    if (k >= n - 1) {
  cout<<"0\n";
  return 0;
}
LD pot = n - k - 1;
RE (i, k + 2) {
  pot /= 2;
}
cout<<pot<<endl;

    Obvious linearity of expectation

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I found a recurrence relation,based on the current length of the string,and current length of the pattern already matched(BW...WB).Can you kindly explain how this closed formula can be derived?

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        There are n - k - 1 positions where this pattern can be matched and probability of occurence in a fixed position is 2 - (k + 2), so result is (n - k - 1)2 - (k + 2)

        → Reply