jgsiqueira's blog

Complicated knapsack problem
By jgsiqueira, 10 years ago, In English

Hi All, i'm trying to solve a problem that remembers knapsack, but a little bit difficult. Can someone help me please? :)

The problem is the following,
There is a diamond mine unexplored. This mine has the shape of a tree.
Each vertex of this tree is a collect point of diamonds, where it is possible to collect X diamonds.
The mine is obstructed. Because of that, we need to dig thru some vertices to reach a collect point of diamonds. There is a cost to dig between to vertices.
You can spend B money units digging the mine, and you want to collect the maximum of diamonds as possible.
Its important to notice that, once dug, you don't need to pay again to pass in an edge.

The picture below shows an example.

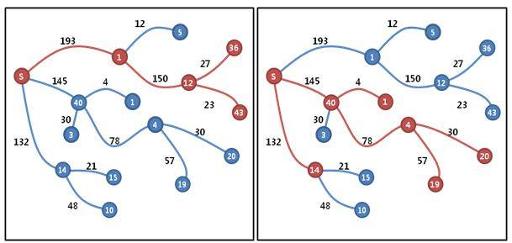
The first picture is the answer for a budget of 400 money units. The second one is the answer for a budget of 450 money units.

[Input] In the first line, the number of diamond collect points N (10≤N≤1,000) and total mining budget (0≤B≤10,000) are given.
In the next N lines, route information (start point, end point), mining cost and benefit of diamonds at the end of the point are given.
All numbers are natural number and they are separated by a space. The mine entrance number is always 0.

  • Vote: I like it
  • +12
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

A solution with dp state dp[budget][node_index] doesn't work?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    There are 107 states so I doubt you have enough time to calculate values for each states.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Hmm, there are also upper and lower bound for each branches? so maybe the states are not that big

      → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Could you explain the exact construction of the DP solution with such state?

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +22 Vote: I do not like it

    It's quite obvious you should make either dp[budget][node] or dp[budget] modified entirely with every new node. Just note the problem is a generalization of knapsack problem (it's exactly a 'knapsack' when we have a worthless root and N-1 leaves). It means that there should be no exact algorithm faster than O(NB).

    However, we need to make these computations very efficient — just because NB can be as large as 107.

    Attempt #1. We want to make a DP on the tree. Each node gets its own table dp[node][budget]: how much diamonds we can get in subtree 'node' if we spend exactly 'budget' (e.g. node 1 gets dp[1][budget]). Leaves are very easy to consider in time O(B). For each internal node we initialize it as if it was a leaf and then add each child sequentially. If 'c' is a child of currently processed 'v', then of course 

    dp'[v][budget>0] = max_{0 <= b <= budget} (dp[v][b] + dp[c][budget-b])
    Let's say this "max-involution" can be done in time T(B) (T is a function). Then it's not hard to see that overall execution time would be O(NT(B)). However, I haven't heard of any algorithms for computing this faster than O(B2). This leaves us with execution time O(NB2), which is clearly too slow. Furthermore, I can't see any way of improving it.

    Attempt #2. We didn't succeed with considering the vertices postorder. Let's try preorder! Let's renumber the vertices in preorder and denote p[v] as parent of vertex v>0 (clearly, p[v] < v). Moreover, we change the definition of dp[budget][node]: it's maximum number of diamonds we can get spending exactly budget if the last taken collect point is node (if it's impossible to spend this amount of money, we set it to  - ∞).

    OK, now we consider node number 'v'. Note that all its ancestors have been already considered. Which previous states we can extend to include 'v'? Of course only these that introduce p[v]. It's not hard to see that these are only the states that the last taken point t is t ≥ p[v] (it's very important and useful!). This way we conclude that 

    dp[budget][v] = max_{p[v] <= t < v} dp[budget-cost[v]][t] + diamonds[v]
    As for now, we've got O(N2B) (for each state, we may have to check O(N) previous states). However, you can note that these states form an interval! That's why for each budget we can make a segment tree (or binary indexed tree) and easily update it for each state. Then we come up with time complexity .

    Attempt #2b. However, there is even faster solution. That's just because we use segment trees only for two queries:

    • add a number to the end of sequence,
    • what is the maximum of the numbers from i-th index to the end of the sequence?

    I won't explain it (at least now), but these queries can also be done in amortized O(α(n)) time (or maybe even faster, but I have no idea now). Then we would come up with an algorithm with time complexity O(NBα(N)) and memory complexity O(NB). It should easily fit in the time and memory limits.

    Can it be done in O(NB) time? I don't know...

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 4   Vote: I like it 0 Vote: I do not like it

      nevermind its incorrect

      → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Wow, that t ≥ p[v] was some pretty clever trickery; that would have never occurred to me at all!

      I think it can be done in O(NB) without any data structures by choosing to do it in postorder. I wrote it as a comment below, in case you want to check it (not having an online judge to test really makes me hesitant about whether my solutions are actually correct or not...).

      → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      There are some thoughts about changing the way of storing and computing dp.
      Suppose we try to store in dp[budget][node] maximum number of diamonds we can get spending exactly budget and the last taken collect point (call it v) is in subtree rooted at node. But to achieve complexity O(NB), we'll store another value: while traversing some vertex u during dfs, dp[budget][node] must contain maximum number of diamonds with the same constraints, but the last taken collect point v must be visited before (i.e. p[node] ≤ p[v] < p[u]). So, calculation in the previous post may be transformed into the following line:

      dp[budget][u] = dp[budget - cost[u]][parent[u]] + diamonds[u]

      And, after visiting all vertices in subtree rooted at u, we must update corresponding values for its parent:

      dp[budget][parent[u]] = max(dp[budget][parent[u]], dp[budget][u])

      So, the overall time complexity is O(NB), isn't it?
      These formulas are almost the same as in ffao's comment http://codeforces.net/blog/entry/13168#comment-179508. It even seems to me that this is the same idea expressed in another way)

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Yes, I believe this is a different explanation for the same idea. Maybe this version is easier to understand, my explanation was quite confusing...

        → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it +5 Vote: I do not like it

There is a relatively simple solution in O(NB) using postorder, I think.

Number every node with a post[node] according to its order in a postorder traversal of the tree.

The trick is: instead of taking dp[k][budget] to be the maximum possible value by using only k's subtree, let dp[k][budget] be equal to the maximum value achievable by using some nodes v such that 0 ≤ v < post[k]. The choices must be made without violating the rule that the parent must be chosen for every chosen node, excluding parents that are ancestors of k.

This way, the update can be done in O(B) per node:

dfs(node):
   initialize dp[node] to dp[parent[node]]
   for every child: dfs(child)
   
   for every budget i:
       dp[parent][i + cost[node]] = max(dp[parent][i + cost[node]], dp[node][i] + diamond[node])
→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    I'm not sure (maybe I don't understand something), but maybe the rule should be rephrased a little: the parent must be chosen for every chosen node, excluding parents that are ancestors of k.

    And sorry, but your pseudocode is incorrect ;(. In the beginning of dfs you erase everything that you've computed for this node so far (these computations were done for the node's children). Maybe it's only a bug, at least I hope so.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Your rephrasing is correct, nice catch.

      The pseudocode seems to be correct as well, as dp[node][x] is updated only by the children of node (and the dfs on the children happens only after the initialization, so nothing was computed when dp is initialized).

      You can check my code for the example tests here.

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it +13 Vote: I do not like it

        OK, sorry for this accusation, I read init dp[parent[node]] to dp[node] and I couldn't make sense of it ;P

        Your code is consistent with my brute-force after fixing a small bug: line 25, replace kn[p[v]][i] with kn[p[v]][i+weight[v]].

        → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    In this solution you are taking only one son or none at all

    → Reply