Given an array of numbers, output the answer to Q queries:
Each query if of the form L, R, X — Find the number of occurences of a[i] in the range [L, R] such that a[i] XOR X is minimum for any i in [L, R]
1 <= N <= 10^6
1 <= X, a[i] <= 10^9
1 <= l <= r <= N
1 <= Q <= 50000











An online solution in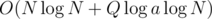 :
:
given a query with X, construct a prefix (from the most significant bit, 29th in this case) of the smallest
X^a[i]in the given range: if you know that the smallest k-bit prefix that can be achieved is p, check if it's possible to achieve a k + 1-bit prefix by appending 0 to p; if it isn't possible, you have to append 1 to phow to check if the most significant k bits can be equal to p: it's equivalent to checking if p appears in the range [L, R) of an array
A[k][i]=a[i]>>(30-k); for each such array, store the positions i on which an element a appears in amap<a,set<i>>, which gives a straighforward way to checkwhen you have the smallest
b=X^a[i], you just need to count how many timesb^X=a[i]appears in that range, which can be done just by augmenting the previous part: for array A[0][], usemap<a,map<i,s>>instead, where s gives the number of times a appeared in positions ≤ i and can be precalculated; then, you just need to find the elements of the innermap<>corresponding to the smallest i ≥ R, ≥ L respectively and subtract their s to find the number of occurences ofb^Xin that range