OIer1048576's blog

[Tutorial] On ordinals
By OIer1048576, history, 4 months ago, In English

Acknowledgements: ChatGPT for Grammar fixing.

In mathematics, ordinals extend the concept of counting beyond finite numbers and incorporate infinite sequences. From a graph theory perspective, you can think of ordinals as a hierarchy of "layers" or "levels" that represent different sizes and types of infinity.

Basic Concepts

In this blog, we define ordinals as competitive graphs $$$\Gamma$$$, where a competitive graph is a directed graph in which exactly one of $$$(u, v)$$$ or $$$(v, u)$$$ is included in the edge set for every pair of distinct vertices $$$u$$$ and $$$v$$$. These graphs are characterized by the absence of loops and reversed rays, where a reversed ray refers to a sequence of vertices $$$v_0, v_1, v_2, \dots$$$ with edges $$$(v_1, v_0), (v_2, v_1), (v_3, v_2), \dots$$$.

Finite ordinals correspond to natural numbers. For instance, $$$0$$$ represents the empty graph, and $$$1$$$ denotes the graph with a single vertex. An example is provided below:

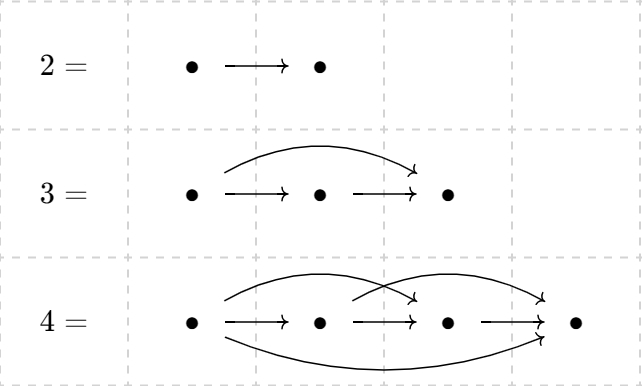
In fact, the set of natural numbers $$$\mathbb{Z}_{\ge 0}$$$, often denoted as $$$\omega$$$, can be interpreted as an ordinal: $$$\Gamma_\omega = (V, E)$$$, where $$$V = \mathbb{Z}_{\ge 0}$$$ and $$$E = \{(i, j) : i < j\}$$$. However, $$$\mathbb{Z}$$$ cannot be considered an ordinal in a similar manner, due to the presence of a reversed ray, as exemplified by the sequence of vertices $$$v_i = -i$$$.

We define $$$\alpha \le \beta$$$ if $$$\beta$$$ can be viewed as a subgraph of $$$\alpha$$$. Similarly, $$$\alpha = \beta$$$ if and only if $$$\alpha \le \beta$$$ and $$$\beta \le \alpha$$$. As is familiar, the relationship between ordinals is either $$$\alpha < \beta$$$, $$$\alpha = \beta$$$, or $$$\alpha > \beta$$$.

Proof (Maybe Mathy)

In fact, for every set $$$A$$$ of ordinals, there exists an ordinal $$$\min A$$$ in the set $$$A$$$. The proof is straightforward: one can obtain $$$\min A$$$ by taking the union of all the $$$S_\alpha$$$, where $$$\alpha \in A$$$ and $$$S$$$ is the set defined previously.

The successor of an ordinal $$$\alpha$$$ is a new graph $$$G$$$ where the vertices include all the vertices of $$$\alpha$$$ along with an additional vertex $$$v$$$. All edges $$$(w, v)$$$, where $$$w$$$ is a vertex in $$$\alpha$$$, are added. The successor of $$$\alpha$$$ is denoted as $$$\alpha^+$$$. It is evident that $$$\alpha < \alpha^+$$$. Consequently, we can define the $$$n$$$-th successor of $$$\alpha$$$, denoted as $$$\alpha + n$$$.

To understand how addition and multiplication of ordinals work, consider the following definitions: For ordinals $$$\alpha$$$ and $$$\beta$$$, $$$\alpha + \beta$$$ is the ordinal with vertices formed by the disjoint union $$$\alpha \sqcup \beta$$$ (where $$$\sqcup$$$ denotes the disjoint union of sets) and edges of three types: the edges from $$$\alpha$$$ itself, the edges from $$$\beta$$$ itself, and new edges $$$(u, v)$$$ where $$$u$$$ is a vertex of $$$\alpha$$$ and $$$v$$$ is a vertex of $$$\beta$$$. Similarly, $$$\alpha \times \beta$$$ is the ordinal with vertices formed by pairs $$$(u, v)$$$, and edges formed by pairs $$$((u, v), (u', v'))$$$, where either $$$(u, u') \in E_\alpha$$$ or $$$u = u'$$$ and $$$(v, v') \in E_\beta$$$.

It is important to note that commutativity does not hold for ordinals: $$$1 + \omega = \omega \ne \omega + 1$$$, and $$$2 \omega = \omega \ne \omega 2$$$. However, associativity does hold.

Here are some properties of ordinals:

  • If $$$\beta < \gamma$$$, then $$$\alpha + \beta < \alpha + \gamma$$$.
  • If $$$\alpha < \beta$$$, there exists a unique $$$\gamma$$$ such that $$$\alpha + \gamma = \beta$$$.
  • For ordinals $$$\gamma$$$ and $$$\alpha$$$, there exists a unique pair of ordinals $$$\beta$$$ and $$$\delta$$$ such that $$$\gamma = \alpha \beta + \delta$$$.
  • For $$$\gamma > 0$$$, there exists a unique Cantor normal form $$$\gamma = \omega^{\alpha_1} k_1 + \dots + \omega^{\alpha_n} k_n$$$, where $$$n \ge 1$$$, $$$\alpha_1 > \alpha_2 > \dots > \alpha_n$$$ are ordinals, and $$$k_1, k_2, \dots, k_n \in \mathbb{Z}_{> 0}$$$.

Application in CP/OI

Consider a directed graph $$$\Gamma$$$ and the SG (Sprague-Grundy) function $$$f$$$ defined on it. If $$$\Gamma$$$ is finite, $$$f$$$ can be easily represented as a natural number-valued function. However, when we extend the SG function to handle infinite graphs, we need to incorporate ordinals.

For instance, in problem 1149E - Election Promises, we observe that a state can have infinitely many successors. To illustrate this, consider the special case where the graph is $$$1 \to 2$$$.

  • If $$$h_1 = 0$$$, then the SG function is $$$h_2$$$, which can be directly verified.
  • If $$$h_1 = 1$$$ and $$$h_2 = 0$$$, the successors are every state $$$0 \to n$$$, where $$$n$$$ is a natural number. Consequently, the SG function for the state $$$h_1 = 1$$$ and $$$h_2 = 0$$$ is $$$\omega$$$, as $$$\omega$$$ is the smallest ordinal not included in $$$\mathbb{N}$$$.

Continuing this pattern, for general values $$$h_1$$$ and $$$h_2$$$, we find that the SG function is given by $$$\omega h_1 + h_2$$$.

More generally, for any directed graph $$$\Gamma$$$ considered as a normal directed graph game, the SG function $$$\sigma$$$ can be expressed in terms of ordinals. Specifically, the SG function can be written as

$$$ \omega^n a_n + \omega^{n-1} a_{n-1} + \dots + a_0, $$$

where the coefficients $$$a_k$$$ are given by

$$$ a_k = \sum_{\sigma(x) = k} h_x. $$$

By fundamental principles in game theory, a game is a P-position (a position from which the second player has a winning strategy) if and only if its SG function is non-zero. This completes the discussion of the problem.

An another example is 最长待机 / Longest Standby.

Translated Statement

Try to solve it yourself! :) After solving it you can understand why $$$1 + \omega \ne \omega + 1$$$.

  • Vote: I like it
  • +18
  • Vote: I do not like it

»
4 months ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by OIer1048576 (previous revision, new revision, compare).

→ Reply
»
4 months ago, # |
  Vote: I like it -19 Vote: I do not like it

easy solution :clown:

#include <algorithm>
#include <cassert>
#include <iostream>
#include <string>
#include <vector>

using namespace std;

struct Tree {
  // Node maximizing the value of depth(l) - 2*depth(v) + depth(r) for l<=v<=r
  struct Node {
    int delta;        // num '(' - num ')'
    int min_depth;    // minimum value of [num '(' - num ')'] on prefix
    int max_depth;    // maximum ...
    int max_lv;       // max value of [depth(l) - 2 * depth(v)], l <= v
    int max_rv;       // max value of [depth(r) - 2 * depth(v)], v <= r
    int max_lvr;      // max value of [depth(l) - 2 * depth(v) + depth(r)]

    static Node Empty() {
      return Node{0, 0, 0, 0, 0, 0};
    }

    static Node LeftParenthesis() {
      return Node{1, 0, 1, 0, 1, 1};
    }

    static Node RightParenthesis() {
      return Node{-1, -1, 0, 2, 1, 1};
    }

    static Node FromCharacter(char ch) {
      if (ch == '(')
        return LeftParenthesis();
      else
        return RightParenthesis();
    }

    Node ShiftHeight(int displacement) const {
      return Node{delta + displacement,
                  min_depth + displacement,
                  max_depth + displacement,
                  max_lv - displacement,
                  max_rv - displacement,
                  max_lvr};
    }

    static Node Merge(const Node &lhs, const Node &rhs) {
      Node rhs_shifted = rhs.ShiftHeight(lhs.delta);

      Node result;
      result.delta = rhs_shifted.delta;
      result.min_depth = min(lhs.min_depth, rhs_shifted.min_depth);
      result.max_depth = max(lhs.max_depth, rhs_shifted.max_depth);
      result.max_lv = max(
          {lhs.max_lv, rhs_shifted.max_lv, lhs.max_depth - 2 * rhs_shifted.min_depth});
      result.max_rv = max(
          {lhs.max_rv, rhs_shifted.max_rv, rhs_shifted.max_depth - 2 * lhs.min_depth});
      result.max_lvr = max(
          {lhs.max_lvr, rhs_shifted.max_lvr,
           lhs.max_lv + rhs_shifted.max_depth,
           rhs_shifted.max_rv + lhs.max_depth});
      return result;
    }
  };

  vector<Node> data;
  int Base;

  Tree(int N) : Base(1) {
    while (Base < N + 1) { Base *= 2; }
    data.resize(Base * 2, Node::Empty());
  }

  void Replace(int pos, char ch) {
    pos += Base;
    data[pos] = Node::FromCharacter(ch);
    pos /= 2;

    while (pos) {
      data[pos] = Node::Merge(data[pos * 2], data[pos * 2 + 1]);
      pos /= 2;
    }
  }

  int GetMaxPath() const {
    return data[1].max_lvr;
  }
};

int main() {
  ios_base::sync_with_stdio(false);
  cin.tie(nullptr);

  int N, Q;
  string paren_string;
  cin >> N >> Q >> paren_string;
  --N;

  Tree path_tree(N * 2);
  for (int i = 0; i < N * 2; ++i) {
    path_tree.Replace(i, paren_string[i]);
  }

  cout << path_tree.GetMaxPath() << "\n";
  for (int query_idx = 0; query_idx < Q; ++query_idx) {
    int first_swap, second_swap;
    cin >> first_swap >> second_swap;
    --first_swap;
    --second_swap;

    const char next_first = paren_string[second_swap];
    const char next_second = paren_string[first_swap];

    assert(next_first != next_second);
    path_tree.Replace(first_swap, next_first);
    paren_string[first_swap] = next_first;

    path_tree.Replace(second_swap, next_second);
    paren_string[second_swap] = next_second;

    cout << path_tree.GetMaxPath() << "\n";
  }
}
→ Reply
»
4 months ago, # |
  Vote: I like it -8 Vote: I do not like it

Auto comment: topic has been updated by OIer1048576 (previous revision, new revision, compare).

→ Reply