This is my version of the editorial for problem D of Codeforces Round 973 (Div. 2). It was motivated by GrishinD's great blog about his solution and presents a slower yet interesting alternative. I wanted to try this exercise to improve my thinking process and maybe become a div1 codeforcer along with GrishinD !

I first had a dynamic programming approach and got TL. Then I tried to work with binary search. I used a constructive algorithm inside the search to check for the validity of the current value. My solution got AC but I wasn't convinced by the correction and I wanted to understand in depth.
This blog explains my solution and brings a comprehensive proof. I'll first describe my algorithm and intuition, and then go through the proof.

Statement

Your are given an array $$$a_1,a_2,…,a_n$$$ of the length n

You can perform any number (possibly, zero) of operations on the array.

In one operation, we choose a position $$$i (1 \leq i \leq n-1)$$$ and perform the following actions:
- $$$a_i:=a_i-1$$$,
- $$$a_{i+1}:=a_{i+1}+1$$$

Find the minimum possible value of $$$max(a_1,a_2,…,a_n)-min(a_1,a_2,…,a_n)$$$

I — Notation and vocabulary

I will use some notations I found useful.
- $$$\forall i, 1 \leq i \leq n$$$ I will denote $$$a_i$$$ as $$$a[i]$$$.
- $$$max(a) $$$ and $$$min(a)$$$ will denote respectively $$$max_{i \in [1, n]}{a[i]}$$$ and $$$min_{i \in [1, n]}{a[i]}$$$

I had a pretty mathematical approach, but I will describe the problem as a line of columns of blocks of size $$$a[i]$$$.

II — Constructive algorithm and intuition

The solution first shows that the smallest maximum (denoted $$$alpha$$$) and the largest minimum obtainable (denoted $$$beta$$$) can be found with binary search in $$$\mathcal{O}(n*log(n))$$$. Then I bring the proof that these two values can be obtained simultaneously using the operation.

I'll describe here my first algorithm used in the binary search to check whether $$$alpha$$$ can be larger than all values of a rearranged $$$a$$$ array.

For $$$i=1$$$ to $$$i=n-1$$$, if $$$a[i] > alpha$$$:
- $$$a[i] := alpha$$$
- $$$a[i+1] := a[i+1] + alpha - a[i]$$$

Note that it is alway a valid algorithm, since it can be decomposed in separation application of the operation.
Visually, the algorithm go through columns from left to right. If a column exceeds $$$alpha$$$, the excedent is reported to the next column.
Let's start with an input array $$$a$$$. The first column excedent is reported to the next, and so on.

Eventually we reach the end of the array

At the end of the loop, $$$alpha$$$ is an admissible majorant iff the last column doesn't exceed $$$alpha$$$. In this case, $$$alpha$$$ is too low, it can't be the smallest minimum.

The same logic can be applied to show that $$$beta$$$ can be the smaller than all values of a rearranged array with the following algorithm

For $$$i=n$$$ to $$$i=2$$$, if $$$a[i] < beta$$$:
- $$$a[i] := beta$$$
- $$$a[i-1] := a[i-1] - (beta - a[i])$$$

Starting from another input array $$$a$$$, the propagation goes backwards :

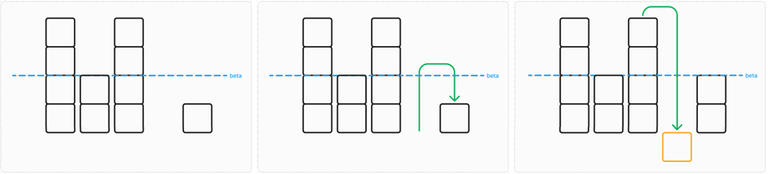
Values in $$$a$$$ can be temporarly negative as shawn in orange, only the value of $$$a[0]$$$ needs to be tested.

At the end of the loop, $$$beta$$$ is an admissible minorant iff the first column is greater or equal than $$$beta$$$. In this case, $$$beta$$$ is can be an admissible minorant.
The proof is similar.

The intuition is then that we can apply the $$$alpha$$$-algorithm and then the $$$beta$$$-algorithm to get a rearranged array with the smallest maximum $$$alpha$$$ and the largest minimum $$$beta$$$. Then the solution of the problem is $$$alpha - beta$$$.

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
typedef unsigned long long ull;

#define forn(i,j,k) for(ll i=(j); i<=(k); i++)
#define rofn(i,j,k) for(ll i=(j); i>=(k); i--)

int main() {
    ll t;
    cin >> t;

    ll n;
    while(t--) {
        cin >> n;
        vector<ll> a(n+1);
        ll mn = 1e15, mx=-1;
        forn(i, 1, n) {
            cin >> a[i];
            mn = min(mn, a[i]);
            mx = max(mx, a[i]);
        }
        
        ll low = mn, high = mx;
        ll alpha, beta;
        while(low+1 < high) {
            alpha = (low + high) / 2;
            ll tmp = 0;
            bool valid = true;
            rofn(i, n, 1) {
                tmp += a[i];
                if(tmp > (n-i+1)*alpha) {
                    valid = false;
                    break;
                }
            }
            if(valid) high = alpha;
            else low = alpha;
        }
        alpha = high;

        low = mn; high = mx;
        while(low+1 < high) {
            beta = (low + high) / 2;
            ll tmp = 0;
            bool valid = true;
            forn(i, 1, n) {
                tmp += a[i];
                if(tmp < i*beta) {
                    valid = false;
                    break;
                }
            }
            
            if(valid) low = beta;
            else high = beta;
        }
        beta = low;

        cout << alpha - beta << endl;
    }
}

It seemed logical at first, but I couldn't be sure of its validity. I took some time to think, and the rest of the blog is a formal proof of this result. Time for the heavy guns.

III — Formal proof of $$$alpha$$$-$$$beta$$$

Previous parts showed that we can find $$$alpha$$$ and $$$beta$$$ with a constructive algorithm starting from the initial array $$$a$$$. The idea of the proof is to show that applying $$$alpha$$$-algorithm yields an array for which it is alway possible to apply $$$beta$$$-algorithm as well.

A — Characterization of admissible maximum and minimum

The first step is to find $$$beta= max(min(\tilde{a}))$$$, where $$$\tilde{a}$$$ is the input array after performing an arbitrary number of operations. This is the largest value that can be obtained for the minimum value in the array $$$a$$$.

For a value $$$beta$$$ to be an admissible minimum of $$$\tilde{a}$$$ is equivalent to this statement : $$$\forall i, 1 \leq i \leq n, \sum_{j=1}^{j=i}{a[j]} \geq i * beta$$$

In other words, the following statements are equivalent

• For any position $$$i$$$, the total amount of blocks left to this position must possible to be less or equal to $$$i$$$ columns of size $$$beta$$$.
  

• The columns $$$1$$$ to $$$i$$$ can be rearranged using the operation to be all greater than $$$beta$$$.
  

Proof

(Note that this applies to the prefix of size $$$k$$$ of $$$\tilde{a}$$$.)

Initialisation

• For $$$k=1$$$, the statement is obvious.
• For $$$k=2$$$, the first column alone has to be larger than i, because it can't ever grow. The second can be smaller, as long as there is enough in a[1]. This writes as : $$$a[1] \geq beta$$$ and $$$a[2] + (a[1] - beta) \geq beta$$$, which is equivalent to $$$(H_2)$$$.

Induction

Suppose $$$(H_k)$$$ is true for an arbitrary value of $$$k$$$. Let's show that $$$(H_{k+1})$$$ is true.

$$$[A \Leftarrow B]$$$ Suppose the right part of $$$(H_{k+1})$$$. If $$$\sum_{j=1}^{j=k+1}a[j] < (k+1)*beta$$$, there is simply not enough blocks left from $$$k+1$$$ for $$$beta$$$ to be an admissible minimum. Therefore, reductio ad absurdum, $$$\sum_{j=1}^{j=k+1}a[j] \geq (k+1)*beta$$$ has to be true.

$$$[A \Rightarrow B]$$$ Suppose the left part of $$$(H_{k+1})$$$. By supposition, we can rearrange $$$a[1], ..., a[k]$$$ to be larger than $$$beta$$$. If $$$a[k+1] \geq beta$$$, the right part of $$$(H_{k+1})$$$ is true. Else,

$$$\sum_{j=1}^{j=k+1}{a[j]} \geq (k+1)*beta \iff \sum_{j=1}^{j=k+1}{a[j]} - k*beta \geq beta \iff \sum_{j=1}^{j=k}{a[j]} - k*beta \geq beta - a[k+1] \geq 0$$$

The sum $$$\sum_{j=1}^{j=k}{a[j]}$$$ represents the excedent left to $$$a[k+1]$$$ after rearranging $$$a[1], ... a[k]$$$ that can be used to get $$$\tilde{a}[k+1] \geq beta$$$

Conclusion

The two statements are equivalent. Moreover, there are also both equivalent to the statement "apply the $$$alpha$$$-algorithm yields a feasible solution". I won't write it again, but a symmetrical proof can be written to prove that the three following statements are equivalent :

• $$$\forall i, 1 \leq i \leq n, \sum_{j=i}^{j=n}a[j] \leq (n-i+1)*alpha$$$
  For any position $$$i$$$, the total amount of blocks right to this position must less or equal to $$$i$$$ columns of size $$$alpha$$$
  

• $$$alpha = max(\tilde{a})$$$
  The columns $$$i$$$ to $$$n$$$ can be rearranged using the operation to be all lower than $$$alpha$$$
  

• The $$$alpha$$$-algorithm yields a valid array for which $$$alpha$$$ is a majorant.
  

The first interesting result is that this prefix (resp. suffix) sum can be used in the binary search for $$$beta$$$ (resp. $$$alpha$$$) instead of building a modified array. But the best is yet to come !

B — Use of smallest maximum and largest minimum in the solution

Finally, this last part shows that we can always rearrange initial $$$a$$$ into an array solution that has both $$$alpha$$$ as maximum and $$$beta$$$ as minimum.

With the optimal $$$alpha$$$ found with binary search and the suffix sum criterion, suppose that we apply $$$alpha$$$-algorithm to the input array $$$a$$$. We will show that it implies that the prefix sum criterion is still respected, and the $$$beta$$$-algorithm can always be applied as well.

$$$beta$$$ being the largest admissible minimum for a rearranged $$$a$$$, the prefix sum criterion is respected before applying $$$alpha$$$-algorithm.
We denote $$$a^{(k)}$$$ the state of the rearranged $$$a$$$ after applying the k-th step of the $$$alpha$$$-algorithm, i.e right after possibly modifying $$$a[k]$$$ and $$$a[k+1]$$$.

Initialisation

$$$(H_1)$$$ : after one step, $$$a^{(k)}[1]$$$ was either set to $$$alpha \geq beta$$$ or kept as $$$a[1] \geq beta$$$.

Induction

Suppose $$$(H_k)$$$ true for a fixed $$$k$$$. Consider $$$(H_{k+1})$$$ :

• either $$$a^{(k)}[k+1] \leq alpha$$$ then $$$a^{(k+1)}[k+1] = a^{(k)}[k+1]$$$, and no blocks were moved after the column $$$k$$$. The prefix sum at index $$$k+1$$$ hasn't changed and the second part of $$$(H_{k+1})$$$ it true as well.
  

• or $$$a^{(k)}[k+1] > alpha$$$, then $$$a^{(k+1)}[k+1] := alpha$$$ and $$$a^{(k+1)}[k+2] := a^{(k)}[k+2] + a^{(k)}[k+1] - alpha$$$.
  

By induction, $$$\sum_{j=1}^{j=k}a^{(k)}[j] \geq k*beta$$$ and $$$a^{(k+1)}[k+1] = alpha \geq beta$$$,
$$$\Rightarrow \sum_{j=1}^{j=k+1}a^{(k+1)}[j] \geq (k+1)*beta$$$.

Conclusion

$$$(H_n)$$$ is true, and the complete application of $$$alpha$$$-algorithm maintains the prefix-sum criterion, so $$$beta$$$ is still the largest minimum possible.
It is possible to search for $$$alpha$$$ and $$$beta$$$ separately, and combine them to build the final answer, $$$alpha-beta$$$.

Thank you for reading it so far, it took me much to much time, but I loved trying to formalize the proof. Let me know if you find mistakes, or simpler way of proving the result.
Thank you I_Love_Diar_Narumov for organizing this contest, and MikeMirzayanov for this great plateform. See ya !