Hi all,
I would like to share with you a part of my undergraduate thesis on a Multi-String Pattern Matcher data structure. In my opinion, it's easy to understand and hard to implement correctly and efficiently. It's (relatively) competitive against other MSPM data structures (Aho-Corasick, suffix array/automaton/tree to name a few) when the dictionary size is specifically (uncommonly) large.
I would also like to sign up this entry to bashkort's Month of Blog Posts:-) Many thanks to him and peltorator for supporting this initiative.
Abstract
This work describes a hash-based mass-searching algorithm, finding (count, location of first match) entries from a dictionary against a string $$$s$$$ of length $$$n$$$. The presented implementation makes use of all substrings of $$$s$$$ whose lengths are powers of $$$2$$$ to construct an offline algorithm that can, in some cases, reach a complexity of $$$O(n \log^2n)$$$ even if there are $$$O(n^2)$$$ possible matches. If there is a limit on the dictionary size $$$m$$$, then the precomputation complexity is $$$O(m + n \log^2n)$$$, and the search complexity is bounded by $$$O(n\log^2n + m\log n)$$$, even if it performs in practice like $$$O(n\log^2n + \sqrt{nm}\log n)$$$. Other applications, such as finding the number of distinct substrings of $$$s$$$ for each length between $$$1$$$ and $$$n$$$, can be done with the same algorithm in $$$O(n\log^2n)$$$.
Problem Description
We want to write an offline algorithm for the following problem, which receives as input a string $$$s$$$ of length $$$n$$$, and a dictionary $$$ts = \{t_1, t_2, .., t_{\lvert ts \rvert}\}$$$. As output, it expects for each string $$$t$$$ in the dictionary the number of times it is found in $$$s$$$. We could also ask for the position of the first occurrence of each $$$t$$$ in $$$s$$$, but the blog mainly focuses on the number of matches.
Algorithm Description
We will build a DAG in which every node is mapped to a substring from $$$s$$$ whose length is a power of $$$2$$$. We will draw edges between any two nodes whose substrings are consecutive in $$$s$$$. The DAG has $$$O(n \log n)$$$ nodes and $$$O(n \log^2 n)$$$ edges.
We will break every $$$t_i \in ts$$$ down into a chain of substrings of $$$2$$$-exponential length in strictly decreasing order (e.g. if $$$\lvert t \rvert = 11$$$, we will break it into $$$\{t[1..8], t[9..10], t[11]\}$$$). If $$$t_i$$$ occurs $$$k$$$ times in $$$s$$$, we will find $$$t_i$$$'s chain $$$k$$$ times in the DAG. Intuitively, it makes sense to split $$$s$$$ like this, since any chain has length $$$O(\log n)$$$.
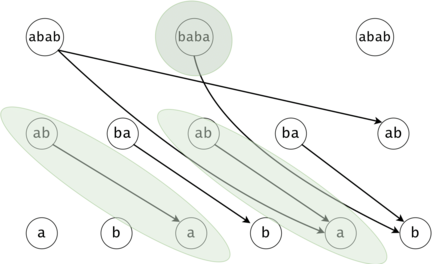
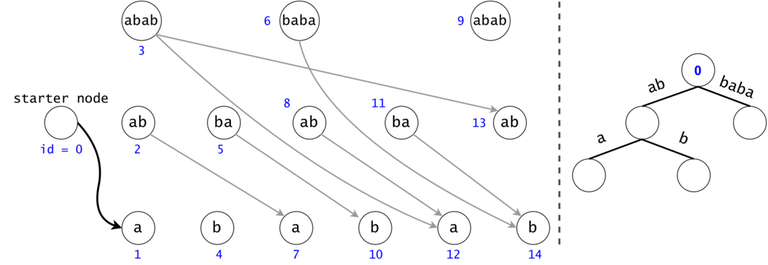
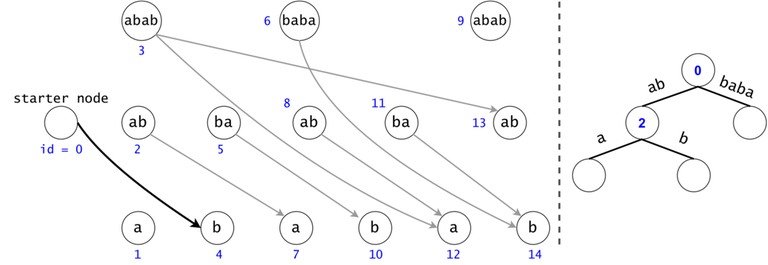
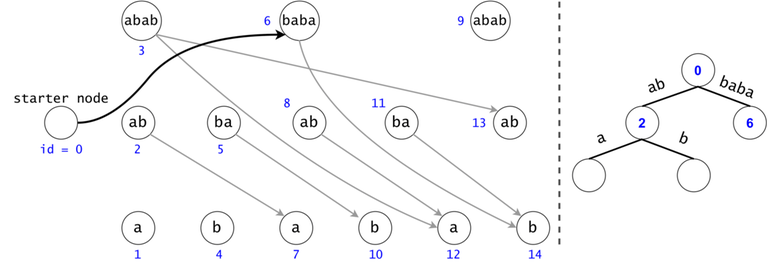
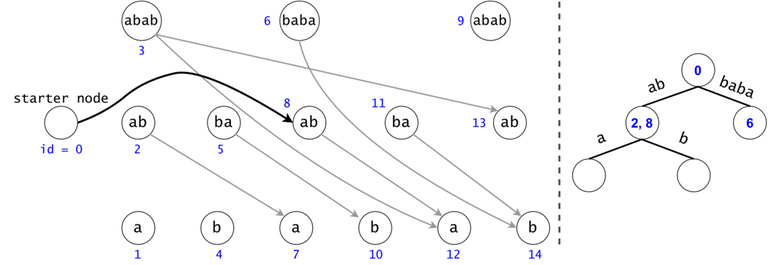
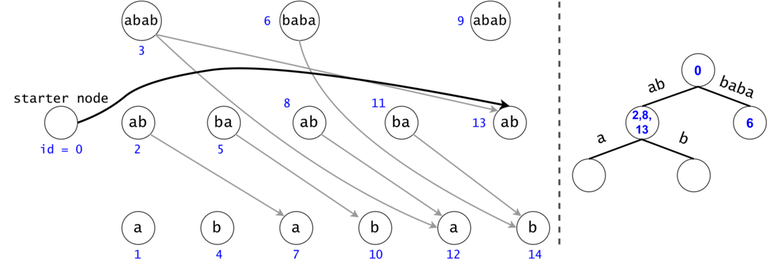
Figure 1: The DAG for $$$s = (ab)^3$$$. If $$$ts = \{aba, baba, abb\}$$$, then $$$t_0 = aba$$$ is found twice in the DAG, $$$t_1 = baba$$$ once, and $$$t_2 = abb$$$ zero times.
Redundancy Elimination: Associated Trie, Tokens, Trie Search
A generic search for $$$t_0 = aba$$$ in the DAG would check if any node marked as $$$ab$$$ would have a child labeled as $$$a$$$. $$$t_2 = abb$$$ is never found, but a part of its chain is ($$$ab$$$). We have to check all $$$ab$$$s to see if any may continue with a $$$b$$$, but we have already checked if any $$$ab$$$s continue with an $$$a$$$ for $$$t_0$$$, making second set of checks redundant.
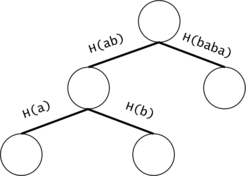
Figure 2: If the chains of $$$t_i$$$ and $$$t_j$$$ have a common prefix, it is inefficient to count the number of occurrences of the prefix twice. We will put all the $$$t_i$$$ chains in a trie. We will keep the hashes of the values on the trie edges.
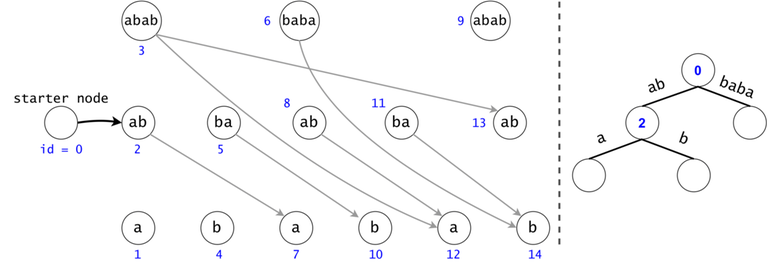
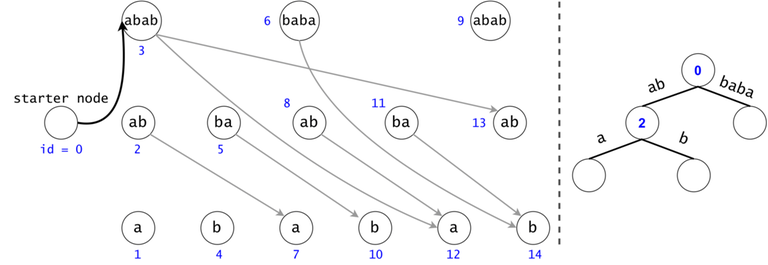
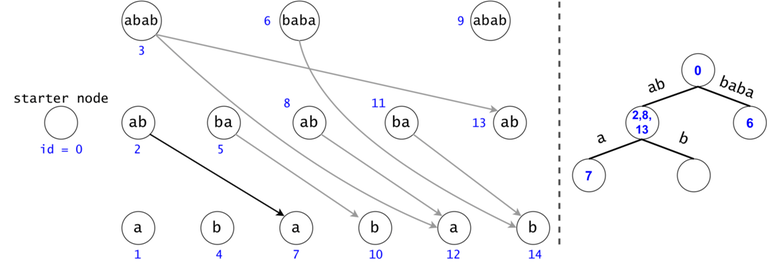
In order to generalize all of chain searches in the DAG, we will add a starter node that points to all other nodes in the DAG. Now all DAG chains begin in the same node.
The actual search will go through the trie and find help in the DAG. The two Data Structures cooperate through tokens. A token is defined by both its value (the DAG index in which it’s at), and its position (the trie node in which it’s at).
Token count bound and Token propagation complexity
Property 1: There is a one-to-one mapping between tokens and $$$s$$$’ substrings. Any search will generate $$$O(n^2)$$$ tokens.
Proof 1: If two tokens would describe the same substring of $$$s$$$ (value-wise, not necessarily position-wise), they would both be found in the same trie node, since the described substrings result from the concatenation of the labels on the trie paths from the root.
Now, since the two tokens are in the same trie node, they can either have different DAG nodes attached (so different ids), meaning they map to different substrings (i.e. different starting positions), or they belong to the same DAG node, so one of them is a duplicate: contradiction, since they were both propagated from the same father.
As a result, we can only generate in a search as many tokens as there are substrings in $$$s$$$, $$$n(n+1)/2 + 1$$$, also accounting for the empty substring (Starter Node's token). $$$\square$$$
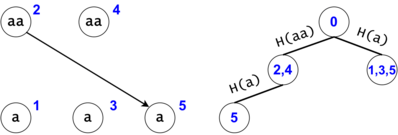
Figure 3: $$$s = aaa, ts = \{a, aa, aaa\}$$$. There are two tokens that map to the same DAG node with the id $$$5$$$, but they are in different trie nodes: one implies the substring $$$aaa$$$, while the other implies (the third) $$$a$$$.
Property 2: Ignoring the Starter Node's token, any token may divide into $$$O(\log n)$$$ children tokens. We can propagate a child in $$$O(1)$$$ (the cost of the membership test (in practice, against a hashtable containing rolling hashes passed through a Pseudo-Random Function)). Therefore, we can propagate a token in $$$O(\log n)$$$, except the starter node's token, which takes $$$O(n \log n)$$$.
As a result, we have a pessimistic bound of $$$O(n^2 \log n)$$$ for a search.
Another redundancy: DAG suffix compression
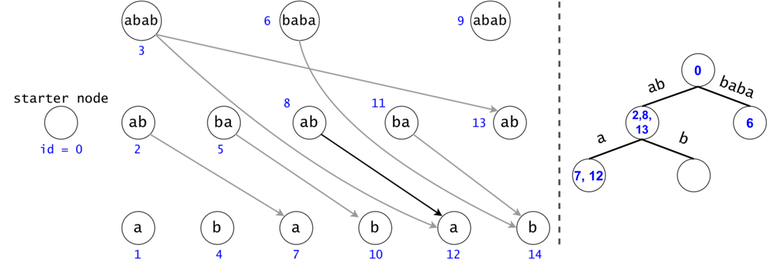
Property 3: If we have two different tokens in the same trie node, but their associated DAG nodes’ subtrees are identical, it is useless to propagate the second token anymore. We should only propagate the first one, and count twice any finding that it will have.
Proof 3: If we don’t merge the tokens that respect the condition, their children will always coexist in any subsequent trie nodes: if one gets propagated, the other will as well, or none get propagated. We can apply this recursively to cover the entire DAG subtree. $$$\square$$$
Intuitively, we can consider two tokens to be the same if they share the present and their future cannot be different, no matter their past.
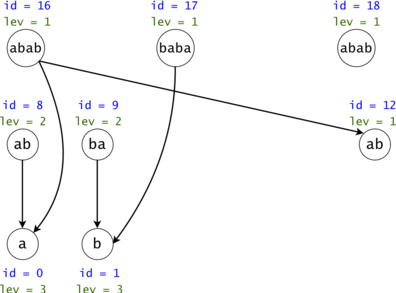
Figure 4: The DAG from Figure 1 post suffix compression. We introduce the notion of leverage. If we compress $$$k$$$ nodes into each other, the resulting one will have a leverage equal to $$$k$$$. We were able to compress two out of the three $$$ab$$$ nodes. If we are to search now for $$$aba$$$, we would only have to only propagate one token $$$ab \rightarrow a$$$ instead of the original two.
Property 4: The number of findings given by a compressed chain is the minimum leverage on that chain (i.e. we found $$$bab$$$ $$$\min([2, 3]) = 2$$$ times, or $$$ab$$$ $$$\min([2]) + \min([1]) = 3$$$ times). Also, the minimum on the chain is always given by the first DAG node on the chain (that isn't the Starter Node).
Proof 4: Let $$$ch$$$ be a compressed DAG chain. If $$$1 \leq i < j \leq \lvert ch \rvert$$$, then $$$node_j$$$ is in $$$node_i$$$'s subtree. The more we go into the chain, the less restrictive the compression requirement becomes (i.e. fewer characters need to match to unite two nodes).
If we united $$$node_i$$$ with another node $$$x$$$, then there must be a node $$$y$$$ in $$$x$$$'s subtree that we can unite with $$$node_j$$$. Therefore, $$$lev_{node_i} \leq lev_{node_j}$$$, so the minimum leverage is $$$lev_{node_1}$$$. $$$\square$$$
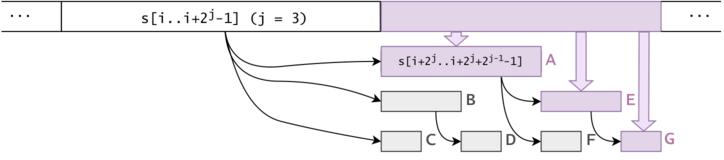
Figure 5: Practically, we compress nodes with the same subtree hash. Notice that the subtree of a DAG node is composed of characters that follow sequentially in $$$s$$$.
Remark: While the search complexity for the first optimization (adding the trie) isn't too difficult to point down, the second optimization (the more powerful DAG compression) is much harder to work with: the worst case is much more difficult to find (the compression obviously has been specifically chosen to move away the worst case))).
Complexity computation: without DAG compression
We will model a function $$$NT : \mathbb{N}^* \rightarrow \mathbb{N}, NT(m) = $$$ if the dictionary character count is at most $$$m$$$, what is the maximum number of tokens that we can generate?
Property 5: If $$$t'$$$ cannot be found in $$$s$$$, let $$$t$$$ be its longest prefix that can be found in $$$s$$$. Then, no matter if we would have $$$t$$$ or $$$t'$$$ in any $$$ts$$$, the number of generated tokens would be the same. As a result, we would prefer adding $$$t$$$, since it would increase the size of the dictionary by a smaller amount. This means that in order to maximize $$$NT(m)$$$, we would include only substrings of $$$s$$$ in $$$ts$$$.
If $$$l = 2^{l_1} + 2^{l_2} + 2^{l_3} + ... + 2^{l_{last}}$$$, with $$$l_1 > l_2 > l_3 > ... > l_{last}$$$, then we can generate at most $$$\Sigma_{i = 1}^{last} n+1 - 2^{l_i}$$$ tokens by adding all possible strings of length $$$l$$$ into $$$ts$$$. However, we can add all tokens by using only one string of length $$$l$$$ if $$$s = a^n$$$ and $$$t = a^l$$$.
As a consequence, the upper bound if no DAG compression is performed is given by the case $$$s = a^n$$$, with $$$ts$$$ being a subset of $$${a^1, a^2, .., a^n}$$$.
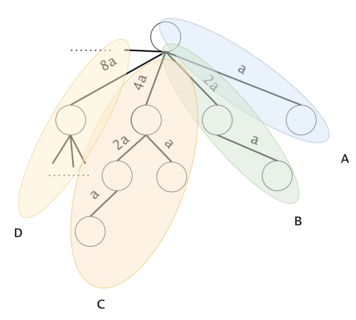
Figure 6: Consider the "full trie" to be the complementary trie filled with all of the options that we may want to put in $$$ts$$$. We will segment it into sub-tries. Let $$$ST(k)$$$ be a sub-trie containing the substrings $$${a^{2^k}, .., a^{2^{k+1}-1}} \,\, \forall \, k \geq 0$$$. The sub-tries are marked here with A, B, C, D, ...}
Property 6: Let $$$1 \leq x = 2^{x_1} + .. + 2^{x_{last}} < y = x + 2^{y_1} + .. + 2^{y_{last}} \leq n$$$, with $$$2^{x_{last}} > 2^{y_1}$$$. We will never hold both $$$a^x$$$ and $$$a^y$$$ in $$$ts$$$, because $$$a^y$$$ already accounts all tokens that could be added by $$$a^x$$$: $$$a^x$$$'s chain in the full trie is a prefix of $$$a^y$$$'s chain.
We will devise a strategy of adding strings to an initially empty $$$ts$$$, such that we maximize the number of generated tokens for some momentary values of $$$m$$$. We will use two operations:
- upgrade: If $$$x < y$$$ respect Property 6, $$$a^x \in ts,\, a^y \notin ts$$$, then replace $$$a^x$$$ with $$$a^y$$$ in $$$ts$$$.
- add: If $$$a^y \notin ts$$$, and $$$\forall \, a^x \in ts$$$, we can't upgrade $$$a^x$$$ to $$$a^y$$$, add $$$a^y$$$ to $$$ts$$$.
Property 7: If we upgrade $$$a^x$$$, we will add strictly under $$$x$$$ new characters to $$$ts$$$, since $$$2^{y_1} + .. + 2^{y_{last}} < 2 ^ {x_{last}} \leq x$$$.
Property 8: We don't lose optimality if we only use add for only $$$y$$$s that are powers of two. If $$$y$$$ isn't a power of two, we can use add on the most significant power of two of $$$y$$$, then upgrade it to the full $$$y$$$.
Property 9: We also don't lose optimality if we upgrade from $$$a^x$$$ to $$$a^y$$$ only if $$$y - x$$$ is a power of two (let this be called minigrade). Otherwise, we can upgrade to $$$a^y$$$ by a sequence of minigrades.
Statement 10: We will prove by induction that (optimally) we will always exhaust all upgrade operations before performing an add operation.
Proof 10: We have to start with an add operation. The string that maximizes the number of added tokens ($$$n$$$) also happens to have the lowest length ($$$1$$$), so we will add $$$a^1$$$ to $$$ts$$$. Notice that we have added/upgraded all strings from sub-trie $$$ST(0)$$$, ending the first step of the induction.
For the second step, assume that we have added/upgraded all strings to $$$ts$$$ from $$$ST(0), .., ST(k-1)$$$, and we want to prove that it's optimal to add/upgrade all strings from $$$ST(k)$$$ before exploring $$$ST(k+1), ...$$$.
By enforcing Property 8, the best string to add is $$$a^{2^k}$$$, generating the most tokens, while being the shortest remaining one.
| operation | token gain | |ts| gain |
|---|---|---|
| add $$$a^{2^{k+1}}$$$ | $$$n+1 - 2^{k+1}$$$ | $$$2^{k+1}$$$ |
| any minigrade | $$$\geq n+1 - (2^{k+1}-1)$$$ | < $$$2^k$$$ |
Afterwards, we gain more tokens by doing any minigrade on $$$ST(k)$$$, while increasing $$$m$$$ by a smaller amount than any remaining add operation. Therefore, it's optimal to first finish all minigrades from $$$ST(k)$$$ before moving on. $$$\square$$$
We aren't interested in the optimal way to perform the minigrades. Now, for certain values of $$$m$$$, we know upper bounds for $$$NT(m)$$$:
| subtries in ts | m | NT(m) |
|---|---|---|
| $$$ST(0)$$$ | $$$1$$$ | $$$n$$$ |
| $$$ST(0), ST(1)$$$ | $$$1+3$$$ | $$$n + (n-1) + (n-2)$$$ |
| $$$ST(0), .., ST(2)$$$ | $$$1+3+(5+7)$$$ | $$$n + ... + (n-6)$$$ |
| $$$ST(0), .., ST(3)$$$ | $$$1+3+(5+7)+(9+11+13+15)$$$ | $$$n + ... + (n-14)$$$ |
| ... | ||
| $$$ST(0), .., ST(k-1)$$$ | $$$1+3+5+7+...+(2^k-1) = 4^{k-1}$$$ | $$$n + ... + (n+1 - (2^k-1))$$$ |
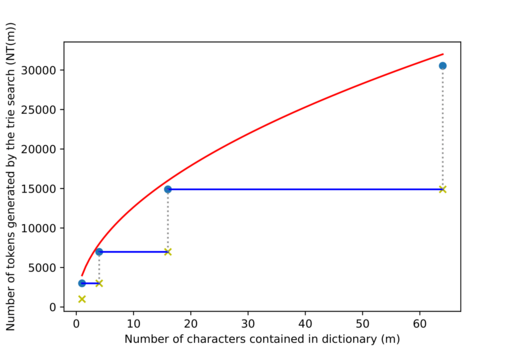
Figure 7: The entries in the table are represented by goldenrod crosses.
We know that if $$$m \leq m'$$$, then $$$NT(m) \leq NT(m')$$$, so we'll upper bound $$$NT$$$ by forcing $$$NT(4^{k-2}+1) = NT(4^{k-2}+2) = ... = NT(4^{k-1}) \,\, \forall \, k \geq 2$$$ (represented with blue segments in figure 7. We will also assume that the goldenrod crosses are as well on the blue lines, represented here as blue dots.
We need to bound:
But if $$$m = 4^{k-1} \Rightarrow 2^{k+1} = 4 \sqrt m \Rightarrow NT(m) \leq n + 4 n \sqrt m$$$.
So the whole $$$NT$$$ function is bounded by $$$NT(m) \leq n + 4 n \sqrt m$$$, the red line in figure 7. $$$NT(m) \in O(n \sqrt m)$$$.
The total complexity of the search part is now also bounded by $$$O(n \sqrt m \log n)$$$, so the total program complexity becomes $$$O(m + n \log^2 n + \min(n \sqrt m \log n, n^2 \log n))$$$.
Corner case Improvement
We will now see that adding the DAG suffix compression moves the worst case away from $$$s = a^n$$$ and $$$ts = \{a^1, .., a^n\}$$$. We will prove that the trie search complexity post compression for $$$s = a^n$$$ is $$$O(n \log^2n)$$$.

Figure 8: A trie node's "father edge" unites it with its parent in the trie.
Statement 11: If a trie node’s "father edge" is marked as $$$a^{2^x}$$$, then there can be at most $$$2^x$$$ tokens in that trie node.
Proof 11: If the "father edge" is marked as $$$a^{2^x}$$$, then any token in that trie node can only progress for at most another $$$2^x-1$$$ characters in total. For example, in figure 8, a token can further progress along its path for at most another three characters, possibly going through $$$a^2$$$ and $$$a$$$.
Since all characters are $$$a$$$ here, the only possible DAG subtree configurations accessible from this trie node are the ones formed from the substrings $$${a^0, a^1, a^2, a^3, ..., a^{2^x-1}}$$$, so $$$2^x$$$ possible subtrees (figure 9).
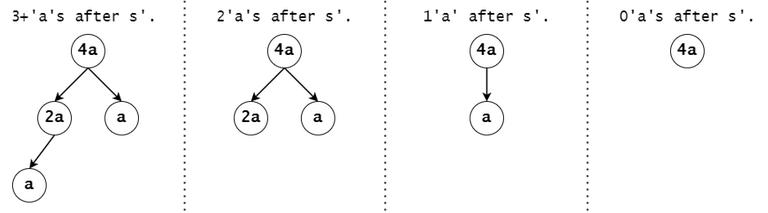
Figure 9: For example, consider a token's associated DAG node with the value of $$$a^4$$$, and $$$s'$$$ to be the substring that led to that trie node (i.e. the concatenation of the labels on the trie path from the root).
If we have more than $$$2^x$$$ tokens in the trie node, then there must exist two tokens who belong to the same DAG subtree configuration, meaning that their nodes would have been united during the compression phase. Therefore, we can discard one of them.
So the number of tokens in a trie node cannot be bigger than the number of distinct subtrees that can follow from the substring that led to that trie node (in this case $$$2^x$$$). $$$\square$$$

Figure 10: For example, the trie search after the DAG compression for $$$s = a^7$$$, $$$ts = {a^1, a^2, .., a^7}$$$.
Let $$$trie(n)$$$ be the trie built from the dictionary $$${a^1, a^2, a^3, ..., a^n}$$$.
Let $$$cnt_n(2^x)$$$ be the number of nodes in $$$trie(n)$$$ that have their "father edge" labeled as $$$a^{2^x}$$$. For example, in figure 10, $$$cnt_7(2^0) = 2^2$$$, $$$cnt_7(2^1) = 2^1$$$, and $$$cnt_7(2^2) = 2^0$$$.
Pick $$$k$$$ such that $$$2^{k-1} \leq n < 2^k$$$. Then, $$$trie(n) \subseteq trie(2^k-1)$$$. $$$trie(2^k-1)$$$ would generate at least as many tokens as $$$trie(n)$$$ during the search.
Statement 12: We will prove by induction that $$$trie(2^k-1)$$$ has $$$cnt_{2^k-1}(2^x) = 2^{k-1-x} \,\, \forall \, x \in [0, k-1]$$$.
Proof 12: If $$$k = 1$$$, then $$$trie(1)$$$ has only one outgoing edge from the root node labeled $$$a^1 \Rightarrow cnt_1(2^0) = 1 = 2^{1-1-0}$$$.
We will now suppose that we have proven this statement for $$$trie(2^{k-1}-1)$$$ and we will try to prove it for $$$trie(2^k-1)$$$.
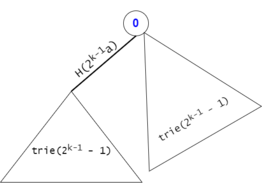
Figure 11: The expansion from $$$trie(2^{k-1}-1)$$$ to $$$trie(2^k-1)$$$.
As a result:
- $$$cnt_{2^k-1}(1) = 2 \cdot cnt_{2^{k-1}-1}(1) = 2^{k-2} \cdot 2 = 2^{k-1}$$$,
- $$$cnt_{2^k-1}(2) = 2 \cdot cnt_{2^{k-1}-1}(2) = 2^{k-2}$$$,
- ...
- $$$cnt_{2^k-1}(2^{k-2}) = 2 \cdot cnt_{2^{k-1}-1}(2^{k-2}) = 2^1$$$,
- $$$cnt_{2^k-1}(2^{k-1}) = 1 = 2^0. \,\, \square$$$
We will now count the number of tokens for $$$trie(2^k-1)$$$:
So there are $$$O(k \cdot 2^{k-1})$$$ tokens in $$$trie(2^k-1)$$$. Since $$$2^{k-1} \leq n < 2^k \Rightarrow k-1 \leq \log_{2}n < k \Rightarrow k \leq \log_{2}n+1$$$.
Therefore, $$$2^{k-1} \leq n \Rightarrow O(k \cdot 2^{k-1}) \subset O((\log_{2}n + 1) \cdot n) = O(n \log n)$$$, so for $$$s = a^n$$$, its associated trie search will generate $$$O(n \log n)$$$ tokens, and the trie search will take $$$O(n\log^2n)$$$.
We can fit the entire program's complexity in $$$O(n\log^2n)$$$ if we give the dictionary input directly in hash chain form.
Complexity computation: with DAG compression
This is the most important part of the blog. We will use the following definitions:
If $$$\lvert t \rvert = 2^{k_1} + 2^{k_2} + 2^{k_3} + ... + 2^{k_{last}}$$$, with $$$k_1 > k_2 > k_3 > ... > k_{last}$$$, then let $$$get(t, i) = t[2^{k_1} + 2^{k_2} + .. + 2^{k_{i-1}} : 2^{k_1} + 2^{k_2} + .. + 2^{k_{i}}], i \geq 1$$$. For example, if $$$t = ababc$$$, $$$get(t, 1) = abab, get(t, 2) = c$$$.
Similarly, if $$$p = 2^{k_1} + 2^{k_2} + .. + 2^{k_{last}}$$$, let $$$LSB(p) = 2^{k_{last}}$$$.
If $$$t$$$ is a substring of $$$s$$$, and we know $$$t$$$'s position in $$$s$$$ ($$$t = s[i..j]$$$), then let $$$shade(s, t) = s[i.. \min(n, j+LSB(j-i+1)-1)]$$$ (i.e. the shade of $$$t$$$ is the content of its DAG node subtree). For example, if $$$s = asdfghjkl$$$, $$$shade(s, sdfg) = sdfg + hjk$$$, $$$shade(s, a) = a$$$, $$$shade(s, jk) = jk + l$$$, $$$shade(s, jkl) = jkl$$$. A shade that prematurely ends (i.e. if $$$n$$$ would be larger, the shade would be longer) may be ended with $$$\varnothing$$$: $$$shade(s, kl) = kl\varnothing$$$.
Let $$$sub(s, t)$$$ denote the number of node chains from $$$s$$$' DAG post-compression whose values are equal to $$$t$$$. For example, $$$sub(abababc, ab) = 2$$$. Notice that $$$sub(s, t)$$$ is equal to the number of distinct values that $$$shade(s, t)$$$ takes.
Let $$$popcount(p)$$$ be the number of bits equal to 1 in $$$p$$$'s representation in base 2.
Statement 13: We choose to classify the trie search tokens in two categories: tokens that are alone (or not alone) in their trie nodes. An alone token describes a distinct substring of $$$s$$$. Thus, it can only have alone tokens as children (their substring equivalent having a distinct prefix of $$$s$$$). We can easily find decent bounds for the number of alone tokens depending of $$$m$$$. We will shortly see that the maximum number of non-alone tokens is relatively small and is independent of $$$m$$$.
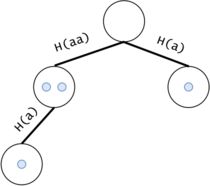
Figure 12: For example, $$$s = a^3$$$ generates two non-alone tokens (for the two $$$a^2$$$s) and two alone tokens (for $$$a^3$$$ and the $$$a$$$ s), not counting the starter node's token.
Statement 14: There are at most $$$O(m)$$$ alone tokens in the trie.

Figure 13: Any $$$t_i$$$ can add at most $$$O(popcount(length(t_i)))$$$ alone tokens in the trie.
Proof 14: For each string in the dictionary, let $$$z_i = \lvert t_i \rvert \,\, \forall \, 1 \leq i \leq \lvert ts \rvert$$$, and $$$z_i = 0 \,\, \forall \, \lvert ts \rvert < i \leq m$$$.
The maximum number of alone tokens in the trie is:
But $$$\Sigma_{i=1}^{m} popcount(z_i) \leq \Sigma_{i=1}^{m} z_i = m$$$, achievable when $$$z_i = 1 \,\, \forall \, 1 \leq i \leq m$$$. $$$\square$$$
The bound is tight for practical values of $$$n$$$ (e.g. generate $$$s$$$ with $$$n = 10^8$$$ such that all substrings of size $$$7$$$ are distinct: $$$\lvert \Sigma \rvert ^ {7} \gg n$$$, even for $$$\lvert \Sigma \rvert = 26$$$. Take $$$ts$$$ to be all $$$s$$$' substrings of size $$$7$$$. Each $$$t$$$ will add at least one alone token, for approximately $$$m/7$$$ alone tokens in total).
Theorem 15: The maximum number of non-alone tokens is $$$O(n \log n)$$$.
Proof 15: Let the number of non-alone tokens generated by $$$s$$$ (considering that $$$ts$$$ contains every substring of $$$s$$$) to be noted with $$$NTna(s)$$$. Also, let the number of alone tokens be noted with $$$NTa(s)$$$: $$$NTna(s) + NTa(s) = NT(s)$$$ (note that we overloaded $$$NT$$$ here).
For example, $$$\max(NTna(s) \mid \lvert s \rvert = 3) = 2$$$, achieved for $$$s = a^3$$$. For longer lengths, there are many patterns that can achieve $$$NTNa(s) \in O(n \log n)$$$, such as $$$a^n$$$, $$$(ab)^k$$$, $$$(ab..z)^k$$$, $$$a^kba^{k-1}ba^{k-2}b...$$$, etc.
We will now redefine the problem of counting the number of non-alone tokens such that it no longer implies a trie search: for a string $$$s$$$, count the substrings $$$t$$$ of $$$s$$$ for which $$$sub(s, t) > 1$$$.
For example, for $$$s = a^3$$$, we won't count the substring $$$a^3$$$ because $$$sub(s, a^3) = 1$$$. We will count both $$$a^2$$$s ($$$s[1 .. 2]$$$ and $$$s[2 .. 3]$$$) because $$$sub(s, a^2) = 2$$$. We won't count any of the $$$a$$$s because they all have the same shade: $$$sub(s, a) = 1$$$. We arrive at $$$NTna(a^3) = 2$$$.
Property 16: Any string $$$s$$$ can be written in the following form: $$$s = s_1^{a_1}s_2^{a_2}s_3^{a_3}...s_k^{a_k}$$$, with $$$s_i \in \Sigma$$$, $$$a_i \geq 1 \,\, \forall \, 1 \leq i \leq k$$$. Also, we choose the representation such that $$$s_i \neq s_{i+1} \,\, \forall \, 1 \leq i < k$$$.
Let $$$f(n) = \max (NTna(s) \mid \lvert s \rvert = n)$$$. We will find a limit for $$$f(n)$$$ through recurrence.
We will split a given $$$s$$$ in two parts: $$$s = s_1^{a_1} + s_2^{a_2}s_3^{a_3}...s_k^{a_k}$$$.
Property 17: $$$NTna(s) \leq NTna(s_1^{a_1}) + 2NTa(s_1^{a_1}) + NTna(s_2^{a_2}s_3^{a_3}...s_k^{a_k}) + 2 \,\, \cdot $$$ the contribution of the substrings that begin in the left hand side (in the first $$$a_1$$$ characters) and end in the right hand side (not in the first $$$a_1$$$ characters).
Proof 17: We will start with $$$s_2^{a_2}s_3^{a_3}...s_k^{a_k}$$$ and build $$$s$$$ by adding $$$s_1^{a_1}$$$ as a prefix. Let $$$S_1$$$ and $$$S_2$$$ be two substrings that are fully contained within $$$s[:a_1]$$$ (i.e. in $$$s_1^{a_1}$$$). We are interested in how do the shades of $$$S_1$$$ and $$$S_2$$$ change post-union with $$$s_2^{a_2}... \,$$$ (can the shades become different if they were equal, or the opposite):
If the shades of $$$S_1$$$ and $$$S_2$$$ are different from the start:
- If exactly one of them prematurely ends (i.e. $$$s_1^{a_1} = a^3$$$, $$$shade(s_1^{a_1}, s_1^{a_1}[1..2]) = a^3$$$, $$$shade(s_1^{a_1}, s_1^{a_1}[2..3]) = a^2\varnothing$$$), then the incomplete shade will contain $$$s_2$$$, which cannot be found in the previously complete shade, which only contains $$$s_1 \neq s_2$$$.
- If both shades prematurely end, then both will look like $$$s_1^?s_2...$$$, but $$$s_2$$$ must occur at different points (because the shades are different, only contain $$$s_1$$$ and end prematurely).
- If no shade prematurely ends, then they cannot be altered post-unite, so the equality status between the shades doesn't change.
If $$$shade(s[:a_1], S_1) = shade(s[:a_1], S_2)$$$, then $$$S_1 = S_2$$$.
- If both shades prematurely end, then $$$S_1$$$ and $$$S_2$$$ describe the same substring, contradiction.
- If no shade prematurely ends, then they cannot be altered post-unite, so the equality status between the shades doesn't change.
- If exactly one shade prematurely ends, then the shades aren't identical, contradiction.
Since the relation between the shades of $$$S_1$$$ and $$$S_2$$$ doesn't change post-appending $$$s_1^{a_1}$$$ to $$$s_2^{a_2}s_3^{a_3}...s_k^{a_k}$$$ for no pair $$$(S_1, S_2)$$$, we can add $$$NTna(s_1^{a_1})$$$ to $$$NTna(s_2^{a_2}s_3^{a_3}...s_k^{a_k})$$$.
However, there may exist "dormant" substrings in $$$s_2^{a_2}...$$$ (i.e. substrings $$$u$$$ for which $$$sub(s_2^{a_2}..., u) = 1$$$, and post-unite $$$sub(s_1^{a_1}s_2^{a_2}..., u) > 1$$$ since $$$u$$$ also exists in $$$s_1^{a_1}$$$ with a different shade, meaning that we have to add $$$1$$$ from behind). As a result, $$$s_1^{a_1}$$$'s alone tokens may become non-alone for $$$s$$$, so we have to count them twice ($$$2NTa(s_1^{a_1})$$$) in order to bound $$$NTna(s)$$$.
A substring of $$$s$$$ that begins in $$$s_1^{a_1}$$$ and ends in $$$s_2^{a_2}...\,$$$ contributes if we can find it again in $$$s$$$, with a different shade. If we can't find it, its associated token is alone for now (dormant). Similarly, we have to double all findings to bound, since each could correspond to a dormant substring from $$$s_2^{a_2}...\,$$$. $$$\square$$$
We will now bound the contribution of the substrings that are not completely contained in one of the two parts.
Let $$$s$$$ be indexed as $$$s[1..n]$$$. Let $$$g = a_1 + 1$$$ be the first index (border) that isn't part of $$$s_1^{a_1}$$$.

Figure 14: We can attempt to include a substring $$$s[l..r]$$$'s contribution only if $$$1 \leq l < g$$$ and $$$g \leq r < n$$$. To actually count it, we have to find $$$s[l..r]$$$ someplace else in $$$s$$$, with a different shade (if we can't do that, it means that $$$s[l..r]$$$ corresponds to an alone token for now).
Generalizing the "someplace else" substrings in $$$s$$$, we have $$$P$$$ pairs $$$(i_p, j_p)$$$ ($$$i_p < g \leq j_p$$$) such that for each $$$1 \leq p \leq P$$$ there exists at least a tuple $$$(x_p, z_p, y_p)$$$ with $$$s[i_p .. g .. j_p] = s[x_p .. z_p .. y_p]$$$ ($$$g - i_p = z_p - x_p$$$). We pick $$$(i_p, j_p)$$$, $$$(x_p, z_p, y_p)$$$ such that the right end of the matching substrings is maximized: either $$$y_p = n$$$, or $$$s[j_p+1] \neq s[y_p+1]$$$.
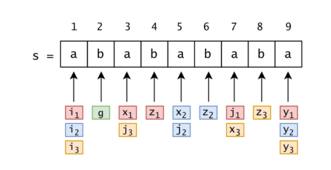
Figure 15: For example, for $$$s = (ab)^4a$$$: $$$n = 9$$$, $$$P = 3$$$, $$$g = 2$$$. $$$(x_1, z_1, y_1) = (3, 4, 9)$$$, $$$(i_1, j_1) = (1, 7)$$$, $$$(x_2, z_2, y_2) = (5, 6, 9)$$$, $$$(i_2, j_2) = (1, 5)$$$, $$$(x_3, z_3, y_3) = (7, 8, 9)$$$, $$$(i_3, j_3) = (1, 3)$$$.
Property 18: $$$x_p > g \,\, \forall \, 1 \leq p \leq P$$$.
Proof 18: If $$$x_p \leq g$$$, then $$$x_p < g$$$ (because $$$s[x_p] = s[i_p] = s_1 (i_p \leq a_1)$$$, and $$$s[g] = s_2 \neq s_1$$$).
If $$$z_p > g$$$, knowing that $$$x_p < g \Rightarrow g \in (x_p, z_p) \subset [x_p, z_p) \Rightarrow s[g] = s_2 \in s[x_p .. z_p-1]$$$, contradiction, $$$s[x_p .. z_p-1]$$$ contains only $$$s_1$$$ characters.
As a result, $$$z_p \leq g$$$. If $$$z_p < g$$$, $$$s[z_p] = s_1 \neq s_2 = s[g]$$$, so $$$z_p = g$$$. Since $$$g - i_p = z_p - x_p \Rightarrow i_p = x_p$$$. We can extend $$$j_p$$$, $$$y_p$$$ as much as possible to the right $$$\Rightarrow j_p = y_p = n$$$. $$$(x_p, z_p, y_p) = (i_p, g, n)$$$ is not a valid interval, being just a copy of the original.
All $$$(x_p, z_p, y_p)$$$ tuples must start after $$$g$$$. $$$\square$$$
For a substring $$$s[l..r]$$$, with $$$l < g$$$, $$$g \leq r$$$, let $$$Q_{l, r}$$$ remember all the pairs that allow $$$s[l..r]$$$ to be found in other places in $$$s$$$:
Property 19: Any substring $$$s[l..r]$$$ that may contribute must fulfill the following two conditions: $$$Q_{l, r}$$$ must not be empty, and for any $$$(i_q, j_q) \in Q_{l, r}$$$, the associated shade of $$$s[l..r]$$$ inside $$$s[x_q..y_q]$$$ must exit $$$[x_q..y_q]$$$.
Proof 19: For the first condition, if $$$Q_{l, r}$$$ is empty, then $$$s[l..r]$$$ cannot be found again in $$$s$$$, meaning that $$$sub(s, s[l..r]) = 1$$$: $$$s[l..r]$$$ will be "dormant" for now, and its contribution may be added on later.
For the second condition, suppose that for some $$$q$$$ for which $$$(i_q, j_q) \in Q_{l, r}$$$, the associated shade of $$$s[l..r]$$$ doesn't exit $$$[x_q..y_q]$$$.

Figure 16: $$$s[l..r]$$$, and its associated substring $$$s[l+x_q-i_q..r+x_q-i_q]$$$.
The associated shade of $$$s[l..r]$$$ ends at:
But the argument of the $$$LSB$$$ function is equal to $$$r-l+1$$$, and if we subtract $$$x_q-i_q$$$ from the inequality:
Meaning that the shade of $$$s[l..r]$$$ also doesn't exit $$$[i_q..j_q]$$$. Since $$$s[i_q..j_q] = s[x_q..y_q]$$$, both of the shades are completely contained within the two intervals and start at the same point relative to $$$i_q$$$ or $$$x_q$$$. The two shades are equal, which means that the contribution of $$$s[l..r]$$$ has already been counted in $$$NTna(s_2^{a_2}s_3^{a_3}...)$$$ (because $$$x_q > g$$$, so $$$s[x_q..y_q] \subset s_2^{a_2}s_3^{a_3}...$$$). $$$\square$$$
We will now simplify and count all substrings that fulfill the previous property. The number of all substrings that qualify is at most equal to the sum of the contributions of all pairs $$$(i_p, j_p)$$$. A substring $$$s[l..r]$$$ contributes for the pair $$$(i_p, j_p)$$$ if $$$i_p \leq l < g$$$, $$$g \leq r \leq j_p$$$, and $$$r + LSB(r - l + 1) - 1 > j_p$$$ (the number of substrings — sum of pair contributions inequality is due to the fact that $$$[l..r]$$$ may be counted by multiple pairs).
Property 20: The maximum number of substrings that can contribute to the pair $$$(i_p, j_p)$$$ is $$$(g-i_p)\log_2(j_p-i_p+1)$$$.
Proof 20: The set of numbers that have their $$$LSB = 2^t, t \geq 0$$$: $$${2^t(2?+1) \mid ? \geq 0}$$$.
For $$$LSB = 2^t$$$: $$$j_p + 1 - 2^t < r \leq j_p$$$. The lower bound is a consequence of the $$$r + LSB(r-l+1) - 1 > j_p$$$ requirement. $$$r$$$ has $$$2^t - 1$$$ possible values.
For a fixed $$$r$$$, let $$$l' < g$$$ be the biggest value $$$l$$$ can take such that $$$LSB(r-l+1) = 2^t$$$. $$$l$$$ could also take the values $$$l' - 2^{t+1}, l' - 2 \cdot 2^{t+1}, l' - 3 \cdot 2^{t+1}, ...$$$ as long as it is at least $$$i_p$$$.
If we decrease $$$r$$$'s values by $$$1$$$, all possible values that $$$l$$$ can take are also shifted by $$$1$$$.

Figure 17: If a slot is marked $$$-k$$$ under the line $$$LSB = 2^t$$$ and column $$$g-z$$$, it means that $$$l$$$ may take the value $$$g-z$$$ if $$$r = j_p - k$$$ (and $$$LSB(r-l+1) = 2^t$$$). For $$$LSB = 2$$$, if $$$r = j_p - 0$$$, $$$l$$$ may take the value $$$g-1$$$ (best case). If it takes $$$g-1$$$, then the next value is $$$g-1 - 2^2 = g-5$$$. It isn't necessary that $$$l' = g - 1$$$ for $$$r = j_p - 0$$$, notice the second line for $$$LSB = 4$$$. The line $$$LSB = 1$$$ is omitted because substrings with $$$LSB = 1$$$ have the shade equal to the substring (so their $$$sub$$$ value is $$$1$$$).
Regardless of the offset (how far away is $$$l'$$$ from $$$g-1$$$) we have for any line $$$LSB = 2^t$$$, we may never overlap two streaks: a streak's length is $$$2^t-1$$$, strictly smaller than $$$2^{t+1}$$$, the distance between two consecutive starts of streaks.
As a result, we may have at most one entry for $$$l$$$ in each slot of the table, meaning that the total amount of valid pairs $$$(l, r)$$$ is at most the number of slots in the table, $$$(g-i_p) \cdot \lfloor log_2(j_p-i_p+1) \rfloor \leq (g-i_p)log_2(j_p-i_p+1)$$$. $$$\square$$$
Remark 21: We could have obviously gotten a better bound (slightly over half of the number of slots), but the added constant over the half becomes a problem later on.
Adding all of the contributions of all pairs $$$(i_p, j_p)$$$ won't produce a good result, even if taking into consideration that $$$\Sigma z_p - x_p \leq n-g$$$. We will now show that we can omit a large amount of pairs from adding their contribution.
Let $$$(i_1, j_1), (i_2, j_2)$$$ be two out of the $$$P$$$ pairs. We will analyze the ways in which $$$[i_1..j_1]$$$ and $$$[i_2..j_2]$$$ can interact:

Figure 18: If $$$i_2 < j_2 < i_1 < g \leq j_1$$$: we have $$$g > j_2$$$, but we need $$$j_2 \geq g$$$, contradiction.

Figure 19: $$$i_2 < i_1 < g \leq j_1 \leq j_2$$$. We have strictness in $$$i_2 < i_1$$$: if $$$i_1 = i_2$$$, then $$$j_1 = j_2 = n$$$ and the pairs wouldn't be different.
$$$[l..r] \subseteq [i_1..j_1] \subset [i_2..j_2]$$$. The shade of $$$s[l..r]$$$ must get out of $$$[i_1..j_1]$$$, as well as $$$[i_2..j_2]$$$: $$$r + LSB(r-l+1) - 1 > j_1$$$, $$$r + LSB(r-l+1) - 1 > j_2$$$.
But since $$$j_2 \geq j_1$$$, only the second condition is necessary. It is useless to count the contribution of the $$$(i_1, j_1)$$$ pair, since any substring $$$s[l..r]$$$ that it may have correctly counted will already be accounted for by $$$(i_2, j_2)$$$.
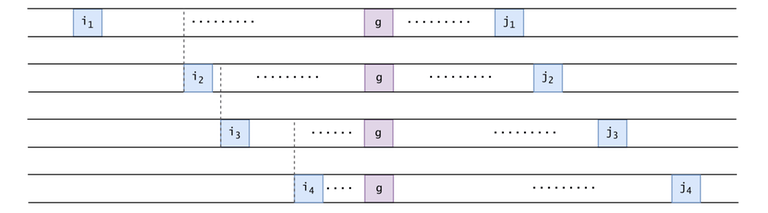
Figure 20: After eliminating all pairs whose intervals were fully enclosed into other pairs' intervals, we are left with this arrangement of intervals: $$$i_{z} < i_{z+1} < g \leq j_z \leq j_{z+1} \,\, \forall \, 1 \leq z < V \leq P$$$.
Let $$$[l..r] \subseteq [i_1..j_1]$$$. If $$$l \geq i_2$$$, then the shade of $$$[l..r]$$$ must also exit $$$[i_2..j_2]$$$ (at least as difficult since $$$j_2 \geq j_1$$$).
Therefore, the only meaningful contribution from $$$(i_1, j_1)$$$ occurs when $$$i_1 \leq l < i_2$$$ and $$$g \leq r \leq j_1$$$, which is at most $$$(i_2 - i_1)\log_2(j_1-i_1+1)$$$.
Generally, the meaningful contribution from $$$(i_z, j_z)$$$ is $$$(i_{z+1} - i_z)\log_2(j_z-i_z+1) \,\, \forall \, 1 \leq z < V$$$.
The sum of contributions is:
But $$$j_z - i_z + 1 \leq n \,\, \forall 1 \leq z \leq V$$$, and $$$g - i_V + i_V - i_{V-1} + .. + i_2 - i_1 = g - i_1$$$, so the sum of contributions is at most:
We know from the Corner Case Improvement section that $$$NTna(s_1^{a_1}) + 2NTa(s_1^{a_1}) \leq 2NT(s_1^{a_1}) \leq 2 \cdot 2a_1 \cdot \log_2(a_1) < 2 \cdot 2g \log_2g$$$. Then:
Because any way we split $$$n$$$ during the recursion, the resulting sum would be $$$6\log_2n \cdot \Sigma g = 6n\log_2n$$$.
The total number of non-alone tokens is $$$O(n \log n)$$$. The total search complexity of the algorithm is $$$O(n\log^2n + m\log n)$$$. $$$\square$$$
Remark 22: Setting up to generate many alone tokens is detrimental to the number of non-alone tokens (generating $$$m/7$$$ alone tokens will give approximately $$$m (popcount(7) - 1) / 7 = 2m/7$$$ non-alone tokens). The opposite is also true. For $$$s = a^n$$$, we will generate close to the maximum amount of non-alone tokens, but only about $$$n/2$$$ alone tokens. This hints to the existence of a better practical bound.
Practical results
We want to compute a practical upper bound for $$$NT(m)$$$. We know a point that has to be on the graph of the $$$NT$$$ function. If $$$\lvert \Sigma \rvert = n$$$, and all characters of $$$s$$$ are pairwise distinct, then if we were to include all substrings of $$$s$$$ into $$$ts$$$, we would generate all of the possible tokens during the search (compression wouldn't help). So $$$NT(n(n+1)(n+2) / 6) = n(n+1)/2$$$.
We want the $$$NT$$$ function to depend on both $$$n$$$ and $$$m$$$, such as $$$NT(m) = ct \cdot n^{\alpha} m^{\beta}$$$. The point we want to fit on $$$NT$$$'s graph would lead to $$$3\beta + \alpha = 2$$$. The easiest idea we could try would be $$$\beta = 1/2 \Rightarrow \alpha = 1/2 \Rightarrow NT(m) = ct\sqrt{nm}$$$. By fitting the known point of $$$NT$$$ we get $$$ct < 1.225$$$. We will also add the $$$O(n \log n)$$$ bias, represented by the number of non-alone tokens. We haven't been able to breach the experimental bound for $$$2 \cdot ct$$$.
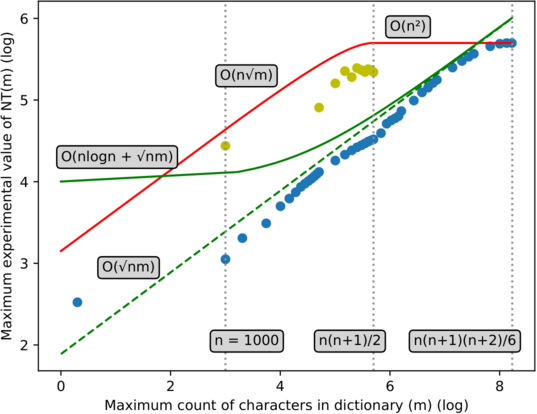
Figure 21: We have fixed $$$n = 1000$$$. Both axes are in logarithmic (base 10) scale.
- The blue dots represent the maximum $$$NT$$$ experimentally obtained for some $$$m$$$ (with compression).
- The goldenrod dots represent the maximum $$$NT$$$ experimentally obtained without compression (the $$$p = {1}$$$ distribution was specifically left out).
- The red line represents the $$$NT$$$ function's bound if no compression is done — $$$O(\min(n\sqrt{m}, n^2))$$$.
- The green line represents the experimental bound for NT: $$$n\log_2n + 2 \cdot 1.225 \cdot \sqrt{nm}$$$.
- The dotted green line represents the unbiased bound: $$$2 \cdot 1.225 \cdot \sqrt{nm}$$$.
The geometric mean in the experimental $$$NT$$$ bound suggests that we would be efficient when $$$m$$$ is much larger than $$$n$$$. In other cases, we would be visibly slower than other MSPMs, since we incur an extra $$$O(\log^2n)$$$ at initialization, and an extra $$$O(\log n)$$$ during the trie search.
We integrated our MSPM into a packet sniffer (snort) as a regex preconditioner. Snort's dictionary is hand-made, only being a couple of MB in size. As a result, most of the computation time (~85%) is rather lost on resetting the DAG upon receiving a new packet. We benchmarked against .pcaps from the CICIDS2017 dataset.
| MSPM type | Friday (min) | Thursday (min) |
|---|---|---|
hyperscan | $$$2.28$$$ | $$$2.09$$$ |
ac_bnfa | $$$3.67$$$ | $$$3.58$$$ |
E3S (aggro) | $$$97.88$$$ | $$$80.74$$$ |
The aggresive variant of the algorithm compresses based on equal DAG node values instead of DAG subtree values, insuring that if $$$t_i \in s$$$, there is exactly one matching chain in the compressed DAG. Previously non-existing DAG chains can appear post-compression, making this variant useful only for $$$t_i \in s$$$ membership queries.
The following two benchmarks are run on synthetic data (to permit higher values of $$$m$$$).
These batches were run on the Polygon servers (Intel i3-8100, 6MB cache), with a $$$15$$$s time limit per test, and a $$$1$$$ GB memory limit per process.
| n | m | type | E3S(s) | AC(s) | suffTree(s) | suffAuto(s) | suffArray(s) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Med | Max | Med | Max | Med | Max | Med | Max | Med | Max | |||
| $$$10^3$$$ | $$$10^8$$$ | 00 | $$$3.0$$$ | $$$3.3$$$ | $$$6.1$$$ | $$$6.9$$$ | $$$0.3$$$ | $$$0.3$$$ | $$$0.5$$$ | $$$0.6$$$ | $$$0.6$$$ | $$$1.0$$$ |
| $$$10^4$$$ | $$$2 \cdot 10^8$$$ | 01 | $$$8.4$$$ | $$$9.0$$$ | TL | $$$1.5$$$ | $$$1.8$$$ | $$$1.9$$$ | $$$2.1$$$ | $$$2.7$$$ | $$$4.0$$$ | |
| $$$10^4$$$ | $$$2 \cdot 10^8$$$ | 11 | $$$7.0$$$ | $$$7.4$$$ | TL | $$$1.0$$$ | $$$1.4$$$ | $$$1.4$$$ | $$$1.5$$$ | $$$3.1$$$ | $$$3.5$$$ | |
| $$$10^4$$$ | $$$2 \cdot 10^8$$$ | 20 | $$$5.1$$$ | $$$5.4$$$ | RE | $$$0.2$$$ | $$$0.5$$$ | $$$1.7$$$ | $$$1.8$$$ | $$$1.5$$$ | $$$1.6$$$ | |
| $$$10^4$$$ | $$$2 \cdot 10^8$$$ | 21 | $$$5.3$$$ | $$$5.6$$$ | TL | $$$0.4$$$ | $$$0.6$$$ | $$$1.0$$$ | $$$1.1$$$ | $$$3.1$$$ | $$$3.2$$$ | |
| $$$10^5$$$ | $$$2 \cdot 10^8$$$ | 00 | $$$9.3$$$ | $$$10.4$$$ | RE | $$$1.0$$$ | $$$5.4$$$ | $$$1.5$$$ | $$$2.9$$$ | $$$1.6$$$ | $$$8.9$$$ | |
| $$$10^5$$$ | $$$2 \cdot 10^8$$$ | 10 | $$$7.7$$$ | $$$8.2$$$ | RE | $$$0.5$$$ | $$$6.5$$$ | $$$1.2$$$ | $$$3.1$$$ | $$$2.0$$$ | $$$8.9$$$ | |
| $$$10^5$$$ | $$$2 \cdot 10^8$$$ | 20 | $$$5.3$$$ | $$$5.4$$$ | RE | $$$0.2$$$ | $$$6.3$$$ | $$$2.1$$$ | $$$4.2$$$ | $$$2.5$$$ | $$$8.9$$$ |
The Aho-Corasick automaton remembers too much information per state (even in an optimized implementation) to fit comfortably in memory for larger values of $$$m$$$.
The following batches were run on the department's server (Intel Xeon E5-2640 2.60GHz, 20 MB cache), with no set time limit, and a $$$4$$$ GB memory limit per process. ML signifies that the process went over the memory limit.
| n | m | type | distribution | E3S(s) | suffArray(s) | suffAuto(s) | suffTree(s) |
|---|---|---|---|---|---|---|---|
| $$$10^5$$$ | $$$2 \cdot 10^9$$$ | 01 | 1 | $$$15.9$$$ | $$$37.5$$$ | $$$9.4$$$ | $$$15.7$$$ |
| $$$10^5$$$ | $$$2 \cdot 10^9$$$ | 21 | 15 | $$$17.7$$$ | $$$17.1$$$ | $$$14.8$$$ | $$$2.0$$$ |
| $$$10^5$$$ | $$$2 \cdot 10^9$$$ | 01 | 27 | $$$30.4$$$ | $$$23.3$$$ | $$$10.4$$$ | $$$23.2$$$ |
| $$$5 \cdot 10^5$$$ | $$$2 \cdot 10^9$$$ | 01 | 27 | $$$40.1$$$ | $$$32.4$$$ | $$$12.1$$$ | $$$26.0$$$ |
| $$$5 \cdot 10^5$$$ | $$$5 \cdot 10^9$$$ | 01 | 27 | ML | $$$74.3$$$ | $$$29.3$$$ | $$$64.1$$$ |
| $$$5 \cdot 10^5$$$ | $$$10^{10}$$$ | 21 | 3 | $$$104.9$$$ | $$$132.5$$$ | $$$61.9$$$ | $$$11.7$$$ |
If $$$m$$$ is considerably large, our algorithm may even do better than a suffix implementation. This usually happens when $$$s$$$ is built in a Fibonacci manner, allowing the compression to be more efficient than expected.
There are large naturally-generated dictionaries: LLM training datasets:-). It is possible (although difficult) to generate some tests which advantage our algorithm:
- $$$s$$$ should be made of $$$P$$$ concatenated LLM answers to
Give me a long quote from "The Hobbit".($$$\lvert s \rvert \simeq P \cdot 1000$$$). - $$$ts$$$ should contain $$$\sim 10^5$$$ sentences from a Book Corpus, along with some substrings from $$$s$$$ ($$$\sim 4 \cdot 10^6$$$ strings in $$$ts$$$).
- We requery $$$ts$$$ with a different $$$s$$$ $$$100$$$ times (advantaging our algorithm and Aho-Corasick, since they don't have to regenerate the dictionary DS).
| P | E3S(s) | AC(s) | suffixArray(s) | suffixAutomaton(s) | suffixTree(s) | processor |
|---|---|---|---|---|---|---|
| $$$5$$$ | $$$55.36$$$ | $$$55.50$$$ | $$$106.85$$$ | $$$156.73$$$ | $$$58.41$$$ | AMD Ryzen 9 3950X |
| $$$10$$$ | $$$106.91$$$ | $$$116.23$$$ | $$$> 180$$$ | $$$> 180$$$ | $$$119.80$$$ | |
| $$$15$$$ | $$$158.58$$$ | $$$171.00$$$ | $$$> 300$$$ | $$$> 300$$$ | $$$183.37$$$ | |
| $$$15$$$ | $$$126.43$$$ | $$$84.93$$$ | $$$257.49$$$ | $$$> 300$$$ | $$$181.245$$$ | Intel Xeon 8480C |
The testing hardware matters in the comparison (likely the cache size matters most, $$$64$$$ MB vs $$$105$$$ MB L3 cache size).
Intersecting datasets likely used for LLM training with LLM output data to infer the amount of memorized (including copyrighted) text is problem receiving a lot of interest lately. We are currently adapting our algorithm to be able to be used in such a problem.
Other applications: number of distinct substrings
We behave like we fill the trie with $$$s$$$' every substring. The number of non-alone tokens is independent of $$$m$$$. The blog is long enough at this point, so figure out yourself how to deal with the alone tokens:-)
Benchmark reproduction
- The github repo can be found here.
- The algorithm implementation can be found here.
- The snort integration code can be found here.
- The next two benchmarks can be reproduced following these instructions.
- Finally, the book citation benchmark can be reproduced by following these instructions.
Acknowledgements
I would like to thank my advisor, Radu Iacob (johnthebrave), for helping me (for a very long time) with proofs, feedback, and insight whenever I needed them. He also pushed for trying the LLM dataset intersection, and found the most favourable benchmark.
I would want to thank popovicirobert, ovidiupita, Daniel Mitra, and Matei Barbu for looking over an earlier version of the work, and offering very useful feedback, as well as Florin Stancu and Russ Coombs for helping me out with various problems related to snort. I would want to thank the team behind CSES for providing a great problem set, and the team behind Polygon for easing the process of testing various implementations.
Thank you for reading this. I hope you enjoyed it, and maybe you will try implementing the algorithm))











Bro, this is codeforces, this is not arxiv.org...
I know, I really wanted to include the proofs://
So you're saying that there is an upper bound on the quality of content that should be posted on CF?
Please realize that by saying this, you're doing nothing to encourage people who write good posts that contribute to the community, and rather discouraging them by sending out the message that such content is not welcome. (At the time of writing, there is not a single constructive comment on this post).
Great high quality blog btw, catalystgma, even though it might be a bit too formal for most people on CF (but I believe reading the whole thing will help them become more mathematically mature, since it also has intuitive explanations in many places). For those who did not read the whole post, this post introduces a new data structure and by going through this, you will likely improve your understanding of string algorithms.
And now I am traumatized T_T
Codeforces Or Algorithm tutorial?
Do I have to write such stuff as undergraduate thesis when I enter collegt?
Seems like really nice blog, will definitely give it chance to read. catalystgma Please ignore negative comments these type of people exists everywhere
I don't think it's negative, it's more like peope mind blown from the depth of the blog. I think it's great
Wake the fuck up samurai
I don't understand any of that but thank you for the high quality blog.
this is great!