kien_coi_1997's blog

Transform Skip list into a BIT with insert operator
By kien_coi_1997, 10 years ago, In English

BIT does not support insert operator, but Skip list does. I realized that we can transform a Skip list into a BIT.

Example source code for impatient people:

http://paste.ubuntu.com/8119698/

My data-structure contains some operators:

  • Insert x v: insert an element valued v into position x:

For instance: {10,20,30} -> insert 40 3 -> {10,20,40,30}

  • Range-sum x y: return sum of elements in ranges x..y

For instance: {10,20,30} -> range-sum 2 3 -> 50

Average complexity of each operator is O(log (max n))

1. Property

a. Parent — child relationship

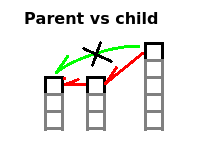
A is parent of B if A is the first node on the right of B and A is not shorter than B (A is higher or at least equal B height).

b. Sum and Count

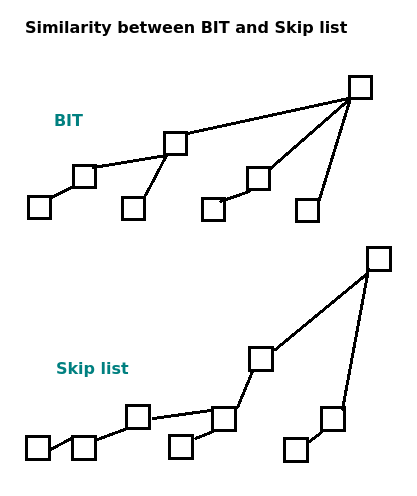
In each node, we maintain a value Sum and Count.

Assume u has children u1, u2, ...

Sum[u] = Value[u] + Value[u1] + Value[u2] + ...

Count[u] = 1 + Count[u1] + Count[u2] + ...

2. Operators

a. Accessing an element x-th

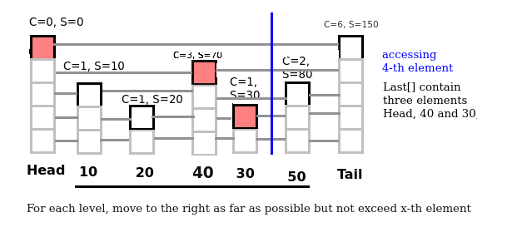
  • For each level (from 19 to 0), we move as far as possible but still not over x-th element (We use value Count in each node to ensure that we not go over x-th element). Additionally, we must keep array Last[] contain id of last element not exceed x-th element (to use this for later operators).

b. Insert an element into position x

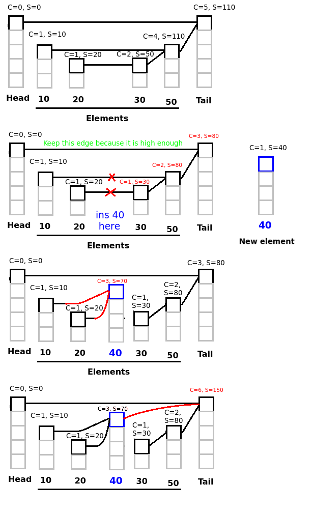
  • Access (x-1)-th element, Last[] let us know edges between (x-1)-th and x-th element.
  • Disconnect short edges (edges which height <= new element's height), maintain Sum and Count of other elements.
  • Insert new element, connect some necessary elements in Last[] with the new element, maintain Sum and Count of relevant elements.
  • Connect new element with its parent, maintain Sum and Count of relevant elements.

c. Get sum of a range

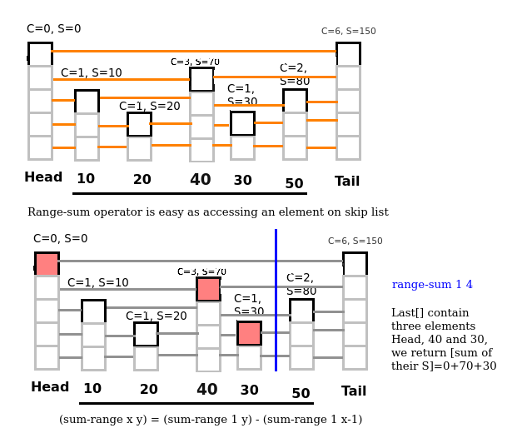
Realize (Range-sum x y) = (Range-sum 1 y) — (Range-sum 1 x-1), therefore we only need to process (range-sum 1 x).

  • Access x-th element
  • Get sum of all of elements in Last[], if an element twice or more, we only plus once.

For example, Last[]={0,0,0,2,3,3,3} -> Answer = Sum[0] + Sum[2] + Sum[3]

3. Example source code

http://paste.ubuntu.com/8119698/

  • I tested it and it worked correctly.
  • It run fast, complexity of each query is about 2.5 * log (max n)
  • Vote: I like it
  • +77
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Nice! Fenwick approach on skip-list looks really easy and intuitive.

Has anyone ever compared skip-lists and cartesian trees (as the most simple self-balancing BST) performance?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thanks. I have tried some benchmark on my computer. Intel Pentium 2.2GHz.

    • q = 100000: 0.38s
    • q = 200000: 0.82s
    • q = 10^6: 5.65s
    → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 2   Vote: I like it +3 Vote: I do not like it 

      do { Level[u]++; } while (rand()&1 && Level[u]<20);

      Looks really inefficient. It's much better to generate random 20-bit integer x and make Level[u] += __builtin_ctz(x) (number of trailing zeros in binary representation of x). This should decrease runtime twice.

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 2   Vote: I like it +8 Vote: I do not like it

        EDIT: Sorry, I have a mistake. Your improvement does not make running time smaller. I used __builtin_ctz(x) but it is wrong, must be __builtin_ctz(x)+1. Running time is still not changed.

        → Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

really awesome tutorial (especially the pictures)! :)

→ Reply