Submission I would like to explain the logic used to solve problem E (which I didn't manage to complete during the contest and submitted shortly after).
For this, it will be useful to know what Catalan numbers are, as well as how to derive their formula. You can read about Catalan numbers in detail, for example, on wiki: click, Catalan numbers can be defined in different ways, but we will define the number $$$C_n$$$ as the number of balanced bracket sequences of length $$$2n.$$$ We are interested in the following relatively well-known and elegant method to find this number.
Let’s consider a coordinate grid where we need to walk from $$$(0,0)$$$ to $$$(n,n)$$$. We can only move to the right or up. A step to the right corresponds to an opening bracket, and a step up — to a closing one. Thus, there is a one-to-one correspondence between a valid bracket sequence of length $$$2n$$$ and a path from $$$(0,0)$$$ to $$$(n,n)$$$ that does not cross the diagonal $$$y=x$$$; since a point above this diagonal would mean that in the current prefix, there are more closing brackets than opening ones. How can we find the number of such paths?
The total number of paths is $$$\binom{2n}{n}.$$$ From this number, we subtract the number of invalid paths. Invalid paths are those that cross $$$y=x$$$, or, equivalently, have at least one common point with the line $$$y=x+1.$$$ Take the first (with the smallest $$$x$$$) common point $$$(a, a+1)$$$ and reflect the segment of the path from $$$(0,0)$$$ to $$$(a, a+1)$$$ across the line $$$y=x+1.$$$ We obtain a path from $$$(-1,1)$$$ to $$$(n,n)$$$. This is a one-to-one correspondence. Indeed, any path starting at $$$(0,0)$$$ that has common points with $$$y=x+1$$$ can be reflected up to the first such point. At the same time, any path from $$$(-1,1)$$$ to $$$(n,n)$$$ must have common points with с $$$y=x+1$$$, since the start and end points of the path are on opposite sides of the line, which means we can also reflect the segment of the path up to the first such point. The number of such invalid paths is $$$\binom{2n}{n+1}.$$$ (or, equivalently $$$\binom{2n}{n-1}.$$$) Therefore, the number of valid paths is $$$C_n = \binom{2n}{n} - \binom{2n}{n+1}.$$$ This is Catalan number. More on the figure below. 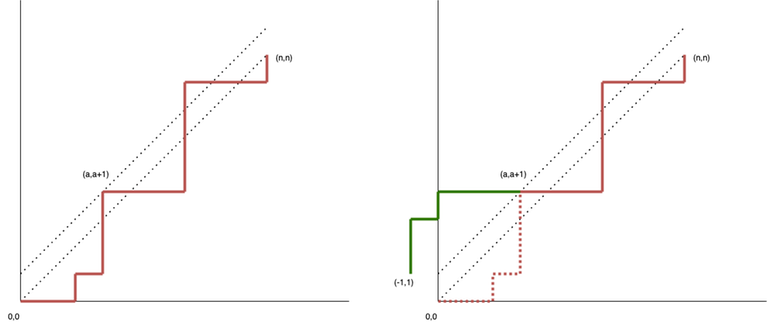
If there were no trump suit in the problem, the winning distribution of cards between the players would satisfy the condition that all cards of the same suit are distributed in the order of a balanced bracket sequence, with $$$m/2$$$ cards for each player. However, the presence of a trump suit requires us to make two modifications to the above formula.
First, suit 1 must still satisfy the prefix condition of a balanced bracket sequence, but it does not have to be completed. Any path from $$$(0,0)$$$ в $$$(a, m-a), a \ge m-a$$$, that does not intersect $$$y=x$$$, satisfies the condition. The number of such paths is $$$\binom{m}{a} - \binom{m}{a+1}$$$. This distribution of suits will leave us with $$$2a - m$$$ trump cards that we can use for other suits. This is the basis of our DP. Let $$$dp_i[ta]$$$ be the number of ways to arrange the first $$$i$$$ suits in a winning way, leaving $$$ta$$$ trump cards available for later use. Then $$$dp_1[2a - m] = \binom{m}{a} - \binom{m}{a+1} \forall a \ge m/2.$$$
Second, if we use $$$k$$$ (even number) trump cards for suit $$$i \ne 1$$$, it means that player 1 plays $$$(m - k)/2$$$ cards of suit $$$i$$$ and player 2 plays $$$(m+k)/2$$$ cards. The cards must satisfy the condition of a "not too imbalanced" bracket sequence, meaning that on any prefix, the number of closing brackets should not exceed the number of opening brackets by more than $$$k.$$$
Combining these ideas, we find that the result is the number of paths from $$$(0,0)$$$ to $$$(\frac{m - k}{2}, \frac{m + k}{2})$$$, that do not intersect $$$y = x + k$$$. Invalid paths are reflected in a similar way as before, but across the line $$$y = x + k + 1$$$, to the paths that start at $$$( -(k+1), (k+1))$$$. Thus the number of valid path is $$$f(m,k) = \binom{m}{(m - k)/2} - \binom{m}{(m - k)/2 + k + 1}$$$. 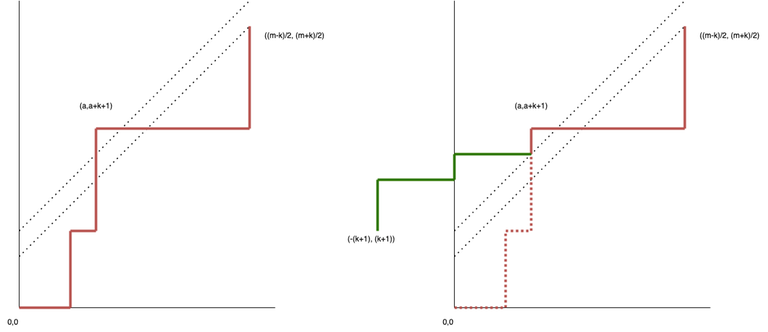
The DP transition itself is easy: $$$\forall ta \le m, \forall k \le ta, dp_i[ta - k] += f(m,k)*dp_{i-1}[ta].$$$ It's enough to consider only even $$$ta$$$ и $$$k$$$. The final answer is $$$dp_n[0].$$$ The complexity is $$$O(m^2n).$$$










The derivation for Catalan numbers is simply amazing, never though it could be explained this way. Next time I need to derive $$$C_n$$$ this will definitely be the first thing that comes to my mind. Thank you so much for the insightful blog.
This distribution of suits will leave us with 2a - m trump cards that we can use for other suits.Sorry if I am wrong, but shouldn't this be
m-2a?No, it's $$$2a -m$$$. If player 1 has $$$a \ge m/2$$$ trump cards, player 2 has $$$m - a$$$ cards, so after matching player 1 left with extra $$$a - (m-a) = 2a -m$$$ trump cards.
Please add this link. If anyone has still problem understading the visualisation, this video might help ...
https://www.youtube.com/watch?v=kaInaIUABzY
very nice explanation , but why is it that when u reflect a path u only reflect on the first intersection point ? reflecting the whole path on the line will give the same result
edit : actually reflecting the whole path does absolutely nothing ignore the above comment
Dude I was almost wondering how you're still Pupil. :-D