snuke's blog

Codeforces Round #263 Tutorial
By snuke, 10 years ago, In English

Div2 A Appleman and Easy Task (Author: EnumerativeCombinatorics)

This is a simple implementation problem. You can solve by searching adjacent cells of every cell.

Div2 B Appleman and Card Game (Author: EnumerativeCombinatorics)

This is simple greedy problem, but it seemed to be reading-hard. The statement says, "Choose K cards from N cards, the score of each card is (the number of cards which has the same character in K cards. (not in N cards)"

It is clear that this total score is (the number of 'A' in K cards)^2 + (the number of 'B' in K cards)^2 + ... + (the number of 'Z' in K cards)^2 This value will be maximized by the simple greedy algorithm, take K cards from most appearred character in N cards, the second most appearred character in N cards, and so on.

Div1 A / Div2 C Appleman and Toastman (Author: hogloid)

First I describe the algorithm, and explain why it works.

  • Sort {ai} in non-decreasing order.
  • Then, for i-th number, add (i + 1) * ai to the result.(i=1...n-1)
  • For n-th number, add n * an to the result.

Actually, when you multiply all numbers by -1,the answer will be the minimal possible value, multiplied by -1.

It's Huffman coding problem to find minimal possible value. Solving Huffman coding also can be solved in O(nlogn)

In Huffman coding, push all the numbers to a priority queue. While the size of the queue is larger than 2, delete the minimal and second-minimal element, add the sum of these two to the cost, and push the sum to the queue. Here, since all the numbers are negative, the pushed sum will be remain in the first in the queue. Analyzing this movement will lead to the first algorithm.

Div1 B / Div2 D Appleman and Tree (Author: hogloid)

Fill a DP table such as the following bottom-up:

  • DP[v][0] = the number of ways that the subtree rooted at vertex v has no black vertex.
  • DP[v][1] = the number of ways that the subtree rooted at vertex v has one black vertex.

The recursion pseudo code is folloing:

DFS(v):
 DP[v][0] = 1
 DP[v][1] = 0
 foreach u : the children of vertex v
  DFS(u)
  DP[v][1] *= DP[u][0]
  DP[v][1] += DP[v][0]*DP[u][1]
  DP[v][0] *= DP[u][0]
 if x[v] == 1:
  DP[v][1] = DP[v][0]
 else:
  DP[v][0] += DP[v][1]

The answer is DP[root][1].

UPD:
The above code calculate the DP table while regarding that the vertex v is white (x[v]==0) in the foreach loop.

After that the code thinks about the color of vertex v and whether we cut the edge connecting vertex v and its parent or not in "if x[v] == 1: DP[v][1] = DP[v][0] else: DP[v][0] += DP[v][1]".

Div1 C / Div2 E Appleman and a Sheet of Paper (Author: snuke)

For each first type queries that p_i > (the length of the paper) — p_i, you should express the operation in another way: not fold the left side of the paper but fold the right side of the paper. After such query you need to think as the paper is flipped.

Let's define count[i] as the number of papers piled up at the segment [i,i+1] (absolute position). For each query of first type you can update each changed count[i] naively.

Use BIT or segment tree for count[i] because you can answer each second type queries in O(log n). The complexity of a first type query is O((the decrement of the length of the paper) log n) so total complexity of a first type query is O(n log n).

Div1 D Appleman and Complicated Task (Author: EnumerativeCombinatorics,snuke)

First, we ignore the already drawn cell and dependence of cells. If we decide the first row, then the entire board can decided uniquely. We call 'o' is 1, and 'x' is 0. Then,

a[i][j] = a[i-2][j] xor a[i-1][j-1] xor a[i-1][j+1]

For example, I'll explain n=5 case. Each column of first row is a, b, c, d, and e. "ac" means a xor c.

a   b   c   d   e
b   ac  bd  ce  d
c   bd  ace bd  c
d   ce  bd  ac  b
e   d   c   b   a

Each character affects the following cells (denoted 'o').

o.... .o... ..o.. ...o. ....o
.o... o.o.. .o.o. ..o.o ...o.
..o.. .o.o. o.o.o .o.o. ..o..
...o. ..o.o .o.o. o.o.. .o...
....o ...o. ..o.. .o... o....

Generally we can prove the dependence that a[0][k] affects a[i][j] if k<=i+j<=2(n-1)-k and |i-j|<=k and k%2==(i+j)%2. ... (*)

We can separate the problems by (i+j) is odd or even.

Each (i,j), we can get the range of k that affects the cell (i,j) by using formula (*). So the essence of this problem is that "There is a sequence with n integers, each of them is 0 or 1. We know some (i,j,k) where a[i]^a[i+1]^...^a[j]=k. How many possible this sequences are there?" We can solve this problem by using union-find. At first, there is n*2 vertices. If k is 1, we'll connect (i*2,(j+1)*2+1) and (i*2+1,(j+1)*2), if k is 0, we'll connect (i*2,(j+1)*2) and (i*2+1,(j+1)*2+1) (note that i<=j). If both i*2 and i*2+1 are in the same set for any i, the answer is 0. Otherwise the answer is 2^((the number of sets-2)/2).

Also, it is possible to solve odd number version. (How many ways to fill all the empty cells with 'x' or 'o' (each cell must contain only one character in the end) are there, such that for each cell the number of adjacent cells with 'o' will be "odd"? ) I'll hope for your challenge for odd-number version!!

Div1 E Appleman and a Game (Author: hogloid,snuke)

Let C be the number of characters(here, C=4)

Given string S, the way to achieve minimum steps is as follows: Append one of the longest substring of T that fits current position of string S. Appending a not-longest substring can be replaced by appending longest substring and shortening the next substring appended.

Let dp[K][c1][c2] be defined as :

the minimum length of string that can be obtained by appending a string K times and that starts by character c1 and whose next character is c2. Note that next character is not counted in the length.

dp[1] can be calculated as follows:

For every string of length L expressed by C characters, if the string is not included in T, update the dp table as dp[1][the string's first character][its last character]=min(dp[1][its first character][its last character],L-1)

For any (c1,c2), dp[1][c1][c2] is smaller than or equal to log_C(T+1)+2 (since the kind of strings of length log_C(T+1)+2 that start by c1 and end by c2 is equals to T+1). Therefore for L=1...log(T+1)+2, try all the strings as described above.

Also we can use trie that contains all substrings of T of length log_C(T+1)+2, and find what can't be described as a substring of T by one step.

Since dp[k+1][c1][c2]=min(dp[k][c1][c3]+dp[1][c3][c2] | c3=1...C), we can use matrix multiplication to get dp[K].

For a integer K, if there is (c1,c2) such that dp[K][c1][c2]<|S|, the answer is greater than K. Otherwise,the answer is smaller than or equal to K.

Since answer is bigger or equal to 1 and smaller or equal to |S|, we can use binary search to find the ansewr.

O(T*((log T)^2+C^2)+C^3(log |S|)^2)

BONUS: Is there any algorithm that solves in O(1) or O(C^foo)(that is, not depended on |S|) for each |S| with pre-calc?

Some hints: Maximal value of dp[1][*][*] — Minimal value of dp[1][*][*] <= 2

(let's call the maximal value dp[1][i][j]=L. Here, any C^(L-2) strings are contained in T as substring, so for any (c1,c2), dp[1][c1][c2]>=L-2)

Maximal value of dp[1][k][*] — minimal value of dp[1][k][*] <=1 ( k=1...C)

Maximal value of dp[1][*][k] — minimal value of dp[1][*][k] <=1 ( k=1...C)

Even if we use these hints and make C=3, the implementation would be not easy.

If you come up with smart way, please comment here :)

  • Vote: I like it
  • +50
  • Vote: I do not like it

Comments Comments (86)
| Write comment?
»
10 years ago, # |
  Vote: I like it -6 Vote: I do not like it

At Div1B/Div2D solution, you say DFS and recursion , but i could not see any recursion function in the code . Btw , is "Pseudo" a new language ? it doesnt get Accepted in any language . what's that ?

:)) good sense of humour

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Sorry, I forgot the function call. Fixed:)

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Pseudo isn't a language that can run. It is a language that can be read easily and understand the algorithm clealy.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      Do you think he is serious? :)

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        FakeErdem and FakeErdem2!!!!! You don't have the right to speak, you CHEATER...

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
          ← Rev. 3   Vote: I like it -57 Vote: I do not like it

          You are green. You are Specialist. You are pochette. Actually, you are the one who doesn't have to right to speak.

          Edit : You are not even Specialist. I realized now, you are Pupil.

          → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it +12 Vote: I do not like it

          I stopped to use them, after I learned it wasn't allow, more than two months ago.

          → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Sorry because of my poor English.

        → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Sorry because of my poor English.

        → Reply
»
10 years ago, # |
  Vote: I like it +5 Vote: I do not like it

So quick editorial. Very thanks.

→ Reply
»
10 years ago, # |
  Vote: I like it +7 Vote: I do not like it

I thought I might give my insight on Div1 A / Div2 C since I wasn't really a fan of the explanation (nor did I understood it properly, although I solved it).

The optimal way to split up into two groups is to leave the smallest number into one group, and all other numbers into a second group. This way you can make sure that you calculate the bigger numbers as much times as possible.

Every number will be calculated at least two times :

  1. When you have only one group of all numbers — the beginning
  2. When you have two groups, one with the smallest number, other with every remaining number

The second smallest number will be calculated three times, the third smallest number four times, and so on until we get down to the last two numbers, which are calculated N times.

Let's check out the test case 

3
3 1 5

Here 1 gets calculated 2 times and 3 and 5 get calculated 3 times, which gives us :

1*2 + 3*3 + 5*3 = 2 + 9 + 15 = 26

Here's a solution in C++ : 7598412

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Same Idea :)

    → Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 4   Vote: I like it 0 Vote: I do not like it

    -blank-

    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I used a dp approach:

    1 — Sort the input.

    2 — Cumulative sum in dp array.

    3 — sol = dp[n]

    4 —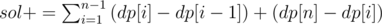

    Here is my Solution

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Where's the proof of correctness for this greedy approach ?

    Calculating the maximum number as many as possible doesn't guarantee that we get the maximum score, because the minimum number will be calculated only 2 times.

    And if we divide them in another way, we can repeat the minimum number more than that.

    so, where's the proof ?

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Not that good at math so I can't give you any better proof than "It passed the tests", but I'll try.

      No matter how you do the splits, you'll always end up summing and splitting 2N-1 groups. It is the same whether or not you always take one number out or always split them in the middle. It might seem that you're always losing a number by taking one out, but by splitting them otherwise you run into situations when you lose two numbers with a single split (while with my way that only happens once).

      The smaller a group is, the closer it is to its members being deleted. So let's say that you sort the group and split it up in middle, then what happens is that you reduce the number of times that the biggest number will be summed and increase the number of times the smallest number will be summed. Now knowing that you haven't increased the number of summations (which I somehow proved above), you can conclude that by not eliminating the smallest number available, you're not achieving optimal results.

      Perhaps someone could give a better explanation if this isn't enough.

      → Reply
»
10 years ago, # |
  Vote: I like it +14 Vote: I do not like it

I haven't understood the idea behind Div1B. Can you elaborate ?

→ Reply
»
10 years ago, # |
  Vote: I like it +7 Vote: I do not like it

I can't understand this sentence "the number of ways that the subtree of vertex v has no black vertex." Somebody rephrase.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +11 Vote: I do not like it

    "the number of ways that the subtree rooted at vertex v can be cut so that the (cut portion) containing the root is only made of white nodes"

    Somebody confirm?

    → Reply
»
10 years ago, # |
  Vote: I like it +6 Vote: I do not like it

If I'm not mistaken, E is pretty straightforward assuming that we have implemented suffix tree (that assumption fails in my case).

Assume that k is the largest number such that all possible words of length k show up as substrings in t. Then, we can simply get that answer is at most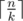 — we simply get k letters in each move. It is also easy to show that answer is at least 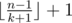, because if C is string of length k + 1 that doesn't appear in t, then C^l demands at least l + 1 moves. k can be very easily determined using suffix tree. So we already have nice bounds for answer.

For simplicity assume that there is such a C of length k + 1 such that its first and last letter is the same, let it be A and let C = AXA, where x is some word. Then make our word s as A(xA)^l. Then we need at least l + 1 moves and this is tight bound.

Now construct a graph on 4 vertices labeled A, B, C, D. Insert edge x->y when if there is a word of length k + 1 starting with x and ending with y such that it doesn't apper as a substring of t. That graph can be easily constructed from suffix tree. Very similar construction as that A(xA)^l can be done if this graph contains a cycle. If not, we need to determine longest path and do something similar. Let this path be A->B->C. Then we construct (AxByC)^l where AxB and ByC are words of length k + 1 which doesn't appear in t. We can't do better then 2(l + 1) in that case and that is also tight bound. Particular answers can be obtained by some not nice computations with ceils depending on the longest path in that 4 vertices graph. Whole solution works in O(|t|)

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it
  1. if x[v] == 1:
  2. DP[v][1] = DP[v][0]
  3. else:
  4. DP[v][0] += DP[v][1]
  5. can anyone explain the condition in else part on line 4 . in question DIV2-D
→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    the edge between v and it's father has two choices , cut or not. if cut, v must connect with some subtree which has black node, so dp[v][0] += dp[v][1];

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      so then how dp[v][0] gives a number of ways such that the subtree rooted at vertex v does not have black vertex ??? if you add the number of ways subtree rooted at v such that has exactly one vertex .

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 3   Vote: I like it 0 Vote: I do not like it

        In the first loop subtrees of vertex v are considered.

        Than the if/else judgement consider vertex v itself.

        If v is black,all of its subtrees should not contain black vertex,so dp[v][1]=dp[v][0].

        If v is white,because dp[v][1] now means one of v's subtrees contain black vertex,so you can just cut the edge between v and this subtrees,so dp[v][0]+=dp[v][1].

        → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      qi ge hao.

      → Reply
»
10 years ago, # |
  Vote: I like it +3 Vote: I do not like it

I solved Div 1 A and B during the contest. However I cannot understand the tutorial for both problems. I implemented an algorithm for Div 1 B that involved integer division and got an AC. Does anyone here share similar solutions to Problem B?

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I solved Div1 A and B during the contest. However I cannot understand the tutorial for both problems. I implemented an algorithm for Div 1B that involved integer division and got an AC. Does anyone here share similar solutions to Problem B?

→ Reply
»
10 years ago, # |
  Vote: I like it +10 Vote: I do not like it

I can't understand the tutorial for the Div1 B. Can anyone explain to me?

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Added the tutorial for Div2 only problems:)

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +25 Vote: I do not like it

    Hm, while ago, I read that post and saw that it has -9 and I thought "downvoting adding tutorials, is CF community serious!?", but when I read those explanations I thought that downvoting this is somehow understandable :P.

    → Reply
»
10 years ago, # |
  Vote: I like it -16 Vote: I do not like it

OMG. Again that's a problem to convince yourself "that brute force works in time".

After reading solution to problem C, I suddenly understood why we can update 1st type operation naively... just some idea of amortized analysis gave O(n log n) complexity for n operations :p

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Bruteforce? Where xd? All Div1 problem had solutions which were clearly sufficiently fast.

    → Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 4   Vote: I like it 0 Vote: I do not like it

    Can you explain please? I am still do not understand, why we can do it naively :|

    I realized, that min(pi, n - pi) wil be fast decrase, right?

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +13 Vote: I do not like it

      Each naive operation corresponds to decreasing width of paper by 1, and its width can't be decreased more than n times.

      → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

I don't get Div1B solution. For white leaves v we've got:

DP[v][1] = 1

In my humble opinion it should be 0, because there's no way that v-subtree has no black vertex. Where am I wrong?

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 8   Vote: I like it +3 Vote: I do not like it

    I had trouble understanding the tutorial's solution as well.

    In my solution, DP[v][k] represents the ways to divide the subtree rooted at v into smaller subtrees such that the subtree rooted at v has k black nodes and the rest of the subtrees all have one black node.

    Then, the pseudocode would be something like this...

    dfs(v)
{
    DP[v][0] = 1 - B[v]
    DP[v][1] = B[v]

    for u : children of v
    {
        old[0] = DP[v][0]
        old[1] = DP[v][1]
        DP[v][0] = DP[v][1] = 0
        
        dfs(u)

        // CASE 1: u is NOT included in the subtree rooted at v
        // Please note that in this case the subtree rooted at u must have one black node,
        // since all the subtrees except the one rooted at v must have one black node

        DP[v][0] += old[0] * DP[u][1]
        DP[v][1] += old[1] * DP[u][1]

        // CASE 2: u is included in the subtree rooted at v
        // In this case, to have one black node in the subtree rooted at v, we either have
        // one black node inside the subtree rooted at u, or we have one outside of it

        DP[v][1] += old[1] * DP[u][0]
        DP[v][1] += old[0] * DP[u][1]

        // Finally, we can have zero black nodes in both of them if u is included

        DP[v][0] += old[0] * DP[u][0]
    }
}

    The answer will be DP[root][1]. I hope I was clearer than the tutorial :P ...

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      thank you

      → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      Thank you very much for your explanation. This makes much more sense than the editorial.

      → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thank you for the beautiful explanation

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Awesome explanation :P

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Each time you are updating DP[v][0] and DP[v][1] values through for loop .Don't you think that the answer will depend on the order of children we choose .

      → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

How to solve div-1 B with ternary search?

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Div1 B / Div2 D Appleman and Tree

How does the function set values for leaf nodes with black color x[v] = 1

so using the code-

DP[v][0] = 1
DP[v][1] = 0

and

if x[v] == 1:
  DP[v][1] = DP[v][0]
 else:
  DP[v][0] += DP[v][1]

DP[v][1] = DP[v][0] = 1

Which means "the number of ways that the subtree rooted at vertex v has no black vertex." = 1 & "the number of ways that the subtree rooted at vertex v has one black vertex." = 1

How is this possible ?

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Duplicate

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

in DIV2-D Can someone tell how are we calculating the results for a vertice from the subtrees of the vertices please?

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

in DIV2-D Can someone tell how are we calculating the results for a vertice from the subtrees of the vertices please?

→ Reply
»
10 years ago, # |
← Rev. 7   Vote: I like it +1 Vote: I do not like it

I think the explanation for Div1B/Div2D is incorrect, or at least poorly worded. It is easy to see that DP[v][0]>=DP[v][1] and it cannot be consistent with the given explanations of DP[v][0] and DP[v][1].

Should it be something like

  • DP[v][0] = the number of ways to cut the subtree rooted at v into components such that the component containing v has at most one black vertex, and all other components have exactly one black vertex.
  • DP[v][1] = the number of ways to cut the subtree rooted at v into components such that the component containing v has exactly one black vertex, and all other components have exactly one black vertex.

?

It is also a pity that the recurrences are given without any formal or informal justifications, which makes them no more useful than someone's code.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +2 Vote: I do not like it

    Yes, that explanation would be easier to understand, but shouldn't DP[v][0] be "the number of ways to cut the subtree rooted at v into components such that the component containing v has ZERO black vertices, and all other components have exactly one black vertex"?

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 14   Vote: I like it 0 Vote: I do not like it

      I am reasonably sure that what is written in DP[v][0] after the entire DFS function is terminated should have at most one black vertex in its description, not zero as it is in the editorial.

      The arguments were shown in the comments above, but I will repeat them here. Consider dfs on a subtree consisting of exactly one black vertex v. For each loop will be skipped, so it the function will terminate with D[v][0] = D[v][1] = 1.

      Basically, from this two statements:

      if x[v] == 1:

      DP[v][1] = DP[v][0]

      else:

      DP[v][0] += DP[v][1]

      it is easy to see that DP[v][0] >= DP[v][1] for any v, that cannot be true for the definition where we have 'ZERO'.

      The invariant for the for each loop however is different:

      Let u1, ..., ui be the vertices iterated over by some iteration i of the loop.

      DP[v][1] contains the number of ways to split the tree rooted at v , where

      1. among all the children, only u1, ..., ui present, other children together with their descendants are temporarily removed,

      2. the vertex v is white, all other vertices has same color as in the input.

      so that the component containing v has exactly one vertex, and all other components have exactly one black vertex.

      Similarly, after iteration i

      DP[v][0] contains the number of ways to split the tree rooted at v , where

      1. among all the children, only u1, ..., ui present, other children together with their descendants are temporarily removed,

      2. the vertex v is white, all other vertices has same color as in the input.

      so that the component containing v has zero black vertices , and all other components have exactly one black vertex.

      After the loop is terminated, we update DP[v][1] and DP[v][0]. In case the vertex is white , we add DP[v][1] to DP[v][0] (and it was assumed to be white in the foreach loop!).

      else:

      DP[v][0] += DP[v][1]

      DP[v][0] will contain exactly the number of ways to split the tree rooted at v , so that the component containing v has either 0 or 1 black vertex (which means at most one):

      If however the vertex v is black, DP[v][1] should contain the same value as DP[v][0]:

      if x[v] == 1:

      DP[v][1] = DP[v][0]

      because there is no way to split the tree into components where the 'upper' one does not have a black vertex:

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 3   Vote: I like it +4 Vote: I do not like it

        Yes, you're right, but I find it very confusing. Why not make DP[v][0] = zero black vertices and DP[v][1] = one black vertex? Not only it's what comes natural, but the relationships would become clearer as well.

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
          ← Rev. 6   Vote: I like it 0 Vote: I do not like it

          This means we will be counting ways with two black vertices.

          No, we won't. We will cut the subtrees counted in DP[u][0] that have a black vertex (i.e, we will cut the edge between u and v for such subtrees) and connect the subtrees counted in DP[u][0] that do not have a black vertex in them to v.

          UPD. I am not sure why the authors decided to use the sum instead of the 'natural' way. Maybe they just wanted to shorten the representation. In all the recurrences we would have the sum of DP[u][0] and DP[u][1] instead of just DP[u][0]. We never need the DP[u][0] itself. It makes it insanely hard to understand the recurrences though. On the other hand, I understand the authors. It seems really difficult to write an editorial using only precise formal language statements (no code). In my writing above I would have to define the terms 'subtree', 'component' to be absolutely accurate. I think they are not understood as meant by most of the people here. And what I wrote is not nearly enough to explain the solution.

          → Reply
          • »
            »
            »
            »
            »
            »
            10 years ago, # ^ |
              Vote: I like it +3 Vote: I do not like it

            Yes, I replied to your comment and then immediately realized that... I edited my comment right after.

            → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can anyone explain the problem of DIV-2 E , how to answer query 2 ?

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

can anyone explain in div-1 D problem how do you get that relation a[i][j]=a[i-2][j]xora[i-1][j-1]xora[i-1][j+1] ????

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    If we use the notations from the editorial ('o' = 1, 'x' = 0), we know from the statement that for (i, j) we have:

    A[i - 1][j]xorA[i + 1][j]xorA[i][j - 1]xorA[i][j + 1] = 0.

    So, for (i - 1, j) we have:

    A[i - 2][j]xorA[i][j]xorA[i - 1][j - 1]xorA[i - 1][j + 1] = 0

    which is equivalent to:

    A[i][j] = A[i - 2][j]xorA[i - 1][j - 1]xorA[i - 1][j + 1].

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      then how you come up with this A[i - 1][j]xorA[i + 1][j]xorA[i][j - 1]xorA[i][j + 1] = 0. can you explain more ???

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it +1 Vote: I do not like it

        A[i][j] = 1 if it contains 'o'

        A[i][j] = 0 if it contains 'x'

        If we have 4 numbers, A B C D, which can be only 0 or 1, AxorBxorCxorD = 0 iff the number of 1s is even.

        → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Please any one explain in Problem DIV1-D @snuke and @EnumerativeCombinatorics how did you get that realation a[i][j] = a[i-2][j] xor a[i-1][j-1] xor a[i-1][j+1] ???

→ Reply
»
10 years ago, # |
  Vote: I like it -21 Vote: I do not like it

Why is 461C so easy? I thought it requires a data structure that supports add part of itself to it. Btw, I think the author's time is O(n*q*logn), it may not pass under 100000 queries"1 50000".

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Can anyone explain problem E of DIV-1 , i am not able to get the idea from the editorial how to solve it? Explain me like a newbie ?? and also in that problem statement it is not given what is "n" ?

→ Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Sorry I would like to ask about the div1-D. How can we get the parity of the variable k in the editorial from the inequality and build the graph.It looks like 2sat but i can't quite understand...

And i looked up some codes which variates from using n to n+2 vertices + dfs to solve , can someone kindly explain a little about their idea .Thank you ...

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    At first, we have variables a, b, c, d, e, f. We split them into two sets: {a, c, e} and {b, d, f}. We solve each half separately. From first set we make new variables {0, a, a xor c, a xor c xor e} = {x1, x2, x3, x4}. Let's assume we have invariant that states c xor e = 1. If x2 equals 0 then x4 should be 1, and if x2 equals 1 then x4 should be 0. So, it is indeed 2sat.

    → Reply
»
10 years ago, # |
  Vote: I like it -8 Vote: I do not like it

mogityant garcheva da mogitynat dedis traki ra aris es bliad??? kide kai ro gavakete B tore eg ro wamekitxa mgitynavdit dedis mutels

→ Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

For 462 Div2A I've seen an interesting solution. When you concatenate all strings and check if this string is a palindrome then the answer will be "YES". I have no idea why these things are connected.

→ Reply
»
11 months ago, # |
  Vote: I like it 0 Vote: I do not like it

hogloid What were you thinking when you wrote an explanation of the Div1/B problem?

→ Reply