Great thoughts come from daily life... XD
Two days ago my classmates(I'm a high school student) invented this easy(but difficult :p) game.. It was just after beginning of new term and they want to find something to do so they create such game imho...
And the rules are at below
Given a N*M board. Each grid contains 1 single piece
Then two players take turns to move away pieces: At each move, he can take any number of pieces in a same row or column (**NOT** necessary to be adjacent ones); The player who takes the last piece wins
Obviously there is a optimal strategy and for given M and N the result is determined(assuming optimal playing), however this is not easy to figure out. Even for small cases(like N=M=4) the game will be very complicated.
So anyone could come up for a solution?











If I am not mistaken, if both N and M are divisible by 2, second player wins, using symmetrical strategy : when first deletes some set of squares, second deletes set of squares, which is got from first set by central symmetry with center in center of board (center of board in this case does not strictly belong to any square).
So, if (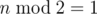 and
and 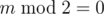 ) or (
) or (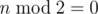 and
and 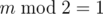 ), first player wins by deleting one row/column and using above strategy on rest of board).
), first player wins by deleting one row/column and using above strategy on rest of board).
I will think about case (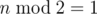 and
and 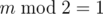 ).
).
The last case is also first player win, since he can just take the center square, then perform the move of the second player, rotated about the center of the board.
EDIT: Never mind, I have misinterpreted the problem, Kaban-5 is correct.
How exactly rotated? By 180 degrees or 90 degrees? In both cases it looks to be not true. May you explain better, please?
For example, you can't win on board 1 X 5 that way (of course, you can take all board, but it is not your strategy), because after you take center, second takes remaining squares and wins.
It appears to work for square boards, if you split the squares into sets likewhere identical letters are paired and no 2 of them are in the same row or column.I still don't get it. How do you answer on second player move
e-g-a(in first column)?Ok, so this doesn't work either :D
There might be a winning strategy for second player in this case sometimes.
I'm sorry about irrelevant question. How can you strikethrough text like your comment.<s></s>tags. Basically any HTML tags work here.Thanksส็็็็็็็็็็็็็็็็็็็( ͡° ͜ʖ ͡°)_ส้้้้้้้้้้้้้้้้้้
I have written a short program. It says that for boards 3 X 3 and 5 X 5 second player wins, but for board 3 X 5 first player wins. So this case seems to be interesting (if, of course, there is not some bug in program, though it works correctly for all small tests, where one of the sides is divisible by 2).
UPD. And for case 3 X 7 first player wins too.
UPD 2. And for board 3 X 9. Unfortunately, even on this test my program works 50 minutes...
EDIT: ignore it, complexity is O((n^(2^m))*C), I have mistakes.
EDIT: I 've tried to strikethrough text in Markdown but I didn't succeed.
There are really that small states (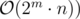 ? It seems to me, that there are not less than
? It seems to me, that there are not less than 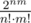 states: each class of equivalent positions contains not more than n!·m! elements (because we have n! permutations of rows and m! permutations of columns), there are 2nm positions (because each positions is subset of (nm)-element set).
states: each class of equivalent positions contains not more than n!·m! elements (because we have n! permutations of rows and m! permutations of columns), there are 2nm positions (because each positions is subset of (nm)-element set).
Of course, some positions are disconnected (so we can use Grundy numbers, and cut amount of equivalent classes), but I still don't understand... For example, for n = m = 15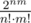 is 43-digit number, even if 10 - 10 of this positions are connected, it is still a lot...
is 43-digit number, even if 10 - 10 of this positions are connected, it is still a lot...
The intention that I post this problem is, in this problem, it's very hard to get split into smaller independent states: if the board can be divided into some independent set of smaller case it should be like
(where 0 denotes a zero matrix)
and looks like very hard to achieve that. And it's also hard to tell if two boards are equivalent. So either Grundy number or prune search doesn't work well.
I've just written a backtrack with optimizations which immediately works on 3x9 and takes a few seconds for 5x7. I noticed an interesting pattern, but I haven't proved it yet (nay, I didn't think about it seriously).
As said above, EVENxEVEN boards are losing because of symmetrical strategy, EVENxODD are winning because we can remove one row and come to the EVENxEVEN game, and ODDxODD are complicated. Say n ≤ m, both of them are odd, n ≠ 1 (because it's a trivial case).
Boards 3x3 and 5x5 are losing. Boards 3x3, ..., 3x13, 5x7 are winning and there is exactly one (up to symmetry) winning move: we should take m - n cells from any row. E.g. the deck 3x7 after the first move looks like this:
I was ready to believe that this pattern always works (because it also explains negative answer for NxN), but... But my program has just found another winning move for 5x9:
The program hasn't stopped yet, so maybe the move given by the pattern is also good. I hope it will finish in a few minutes. Also I'm now computing 7x7, and no winning moves have been found yet.
Unfortunately, the pattern does not work for 5x7: backtrack has found one more winning move and stopped. Here it is:
It took 843 seconds to compute 5x7 pattern, btw.
Can you share some part of your searching method? I cannot get an idea better than brute-force search+AlphaBeta method
I do a backtracking with some optimizations. They are quite simple, actually: precompute all possible moves and split masks into equivalency classes (i.e. sort all rows and columns). A state is a 64-bit integer, of course. One more thing I tried to do is sort moves by the number of affected cells (try to cut more cells first) but it didn't help much.
I don't understand how to use alpha-beta method here because it is a win/lose game and alpha-beta helps when we optimize gained points.
You may take a look at the code.
Wow. Seems like this topic is a huge success XD
Actually creating board games is a interest for us :D but we have never got such a complicated problem. Some previous problems are quite easy that someone who even doesn't know game theory, can come up with an answer by just using math/logic, within a single hour.
And we never expected to get a long lasting problem (And that's good! that means we can keep playing this game; If an optimal strategy for general case is found then why going on?)