Assume that the number of colors $$$c$$$ is fixed. Let $$$mx[i][j]$$$ represent the length of the continuous path ending at node $$$i$$$ with color $$$j$$$. How do we construct $$$mx$$$?

Let's try some approaches. For the connected component formed by the first $$$k$$$ nodes, we can use color 1 for all of them. In this case, the $$$i$$$-th node's $$$mx$$$ array (for $$$1 \le i \le k$$$) would be:
$$$mx[i] = [ i-1 ,0, \dots, 0]$$$.

For the $$$(k+1)$$$-th node, we can use color 2 to connect the connected component formed by the first $$$k-1$$$ nodes. Thus, the $$$(k+1)$$$-th node's $$$mx$$$ array would be:
$$$mx[k+1] = [0, 1, 0, \dots, 0]$$$.

For the $$$(k+2)$$$-th node, we can use color 2 to connect the connected component formed by the first $$$k-1$$$ nodes and color 1 to connect node $$$k$$$. In this case, the $$$(k+2)$$$-th node's $$$mx$$$ array would be:
$$$mx[k+2] = [1, 1,0, \dots, 0]$$$.

At this point, you might realize: The $$$i$$$-th node's $$$mx$$$ array is exactly the $$$(i-1)$$$ in base $$$k$$$ as a mask!

Claim $$$1$$$: for two indices $$$i$$$ and $$$j(i<j)$$$, $$$mx[i] \neq mx[j]$$$.

Proof $$$1$$$: if we use color $$$k$$$ to connect node $$$i$$$ and $$$j$$$, $$$mx[i][k]+1=mx[j][k]$$$ must hold.

So we can assign values to each node's $$$mx$$$ array using a $$$k$$$-base mask from $$$0$$$ to $$$n-1$$$, which gives us a lower bound on the answer.

Claim $$$2$$$: we can always reach this lower bound.

Proof $$$2$$$: for two indices $$$i$$$ and $$$j(i<j)$$$, find $$$k$$$ such that $$$mx[i][k]<mx[j][k]$$$, then use color $$$k$$$ to connect node $$$i$$$ and $$$j$$$.

277722333

• $$$a[1][2]=a[2][1]=a[n-1][m]=a[n][m-1]='.'$$$ must hold.

• We can simply find the shortest path using BFS.

• Robot B can follow behind Robot A. That is, Return to $$$(1,1)$$$ in two steps, then "track" A. So the lower bound of our answer is the shortest path length+2.

• The only remaining problem is: how to find two disjoint shortest paths?

To to find two disjoint shortest paths, we have a classic idea: only walk along the edge of the shortest path tree.

That is, note $$$dis[x]$$$ as the distance from $$$s$$$ to $$$x$$$, we only remain edges $$$u \rightarrow v$$$ such that $$$dis[u]+1=dis[v]$$$.

Official editorial said:

Once all cells on the shortest path are known, sort them by their distance to $$$(1, 1)$$$, i.e., $$$d_1(x, y)$$$ values. Now, if there’s any “level” of the shortest path that contains exactly one cell, every shortest path much pass through this cell and two disjoint paths cannot exist. Otherwise, a valid pair of paths will always exist.

I am confused about how to prove this. After thinking, I came up with a rigorous proof using the maximum flow minimum cut theorem.

Since each node can be visited at most once, we need to split node $$$x$$$ into $$$x$$$ -> $$$x'$$$ when constructing the flow graph. Let's say $$$dis[x]=dis[x']$$$.

What I want to prove is that if the number of nodes at all "levels" is greater than $$$1$$$ (except for $$$s$$$ and $$$t$$$), then for all cuts, the number of cut edges is always greater than $$$1$$$.

Let $$$D[i]$$$ be the set of all nodes $$$x$$$ such that $$$dis[x] = i$$$.

Assume we can find a $$$D[i]$$$ satisfying there are two nodes $$$u,v∈D[i]$$$, such that $$$u∈S$$$ and $$$v∈T$$$ (let's call it "impure"). According to our assumption, there are at least two pairs of $$$x$$$->$$$x'$$$ in $$$D[i]$$$. We will discuss three cases.

• Case $$$1$$$: $$$x$$$ and $$$x'$$$ are from different $$$S/T$$$ sets. In this case, $$$x$$$->$$$x'$$$ is already a cut edge.

• Case $$$2$$$: $$$x$$$ and $$$x'$$$ are both from $$$S$$$. In this case, by following the successors of $$$x'$$$, we can always find a cut edge.

• Case $$$3$$$: $$$x$$$ and $$$x'$$$ are both from $$$T$$$. In this case, by following the predecessors of $$$x$$$, we can always find a cut edge.

In this way, we can always find at least two different cutting edges. Q.E.D.

If we can't find "impure" $$$D[i]$$$, this case is easier — we can find two cutting edges between some $$$D[i]$$$ and $$$D[i+1]$$$. The proof are left to you :)

Note $$$|D[i]|$$$ as the number of nodes of $$$D[i]$$$($$$s$$$ and $$$t$$$ are excluded). If $$$min(D[i])=k$$$, can we find $$$k$$$ disjoint shortest path for any $$$k$$$?

No. It only holds when $$$k=2$$$.

The following is the counter case for $$$k=3$$$:

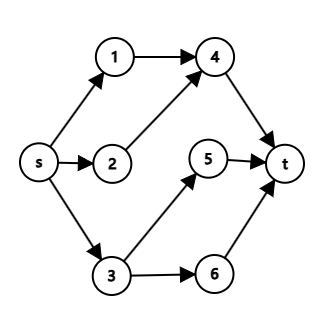
After retaining only the edges on the shortest path tree, we can run a maximum flow algorithm to check if the maximum flow is $$$2$$$. Due to the special nature of the graph, the time complexity is equivalent to performing two BFS traversals on the graph.

We construct the Cartesian tree of the array, where $$$maxa$$$ is the root.

We can think of the process of merging numbers as one slime eating another slime.

If you are at slime $$$a[x]$$$, what would you do? First, you can definitely eat the subtree you are in. After that, you try to eat your parent. If you can do so ($$$subtreesum[x] \ge a[fa[x]]$$$), it is equivalent to being in the position of slime $$$fa[x]$$$. Otherwise, mark the edge $$$(x, fa[x])$$$ as a "blocking edge." We use DSU to link all non-blocking edges, and the size of the set containing the root is the answer.

Maintain the Tree with Data Structures.

We first construct the Cartesian tree for $$$a[1...n]$$$, using a segment tree to maintain its Euler sequence. Some arrays and DSU also needed. Afterward, we "clear" it—set all values in the segment tree to 0, and disconnect every point in the DSU. Then, we add the nodes one by one.

We can also use arrays $$$fa$$$, $$$lc$$$, and $$$rc$$$ to maintain the current parent-child relationships in the tree. When adding $$$a[i]$$$, we set the value at position $$$i$$$ in the segment tree to $$$a[i]$$$ and check whether the edge between $$$i$$$ and its child(at most two children) is a "blocking edge". If it is not, we use DSU to merge $$$i$$$ and $$$a[i]$$$. This step is not hard.

Additionally, all edges on the path from $$$a[i]$$$ to the root may change from being "blocking edges" to "non-blocking edges" (but "non-blocking edges" will never become "blocking edges"—think about why). We check all edges on the path from $$$a[i]$$$ to the root and update them using DSU.

In DSU, for the nodes in the same set, we can maintain the point with the smallest depth in that set. This allows us to quickly skip over many consecutive "non-blocking edges".

For a "blocking edge", it may be checked many times. If there are many "blocking edges" on a path to the root, and after checking they do not change, could we check $$$O(n^2)$$$ times?

No. For a path to the root, there can be at most $$$O(\log n)$$$ "blocking edges."

Why? Let's review: a "blocking edge" $$$(x, fa[x])$$$ is an edge that satisfies $$$subtreesum[x] < a[fa[x]]$$$. Each time we pass through a "blocking edge", the subtree sum at least doubles. Therefore, there can be at most $$$O(\log n)$$$ "blocking edges."

291785878