cgy4ever's blog

Codeforces Round #290 Editorial
By cgy4ever, 10 years ago, In English

Update 1 : here are the reference solutions for this contest:

  1. Div2-A: http://ideone.com/JP1Ksj
  2. DIv2-B: http://ideone.com/udz3bN
  3. Div2-C / Div1-A: http://ideone.com/KVobNb
  4. Div2-D / Div1-B: http://ideone.com/7MQqOm
  5. Div2-E / Div1-C: http://ideone.com/z3FsU2
  6. Div1-D: http://ideone.com/Y7j21a
  7. Div1-E: http://ideone.com/Orbacp

Note that for Div2-E / Div1-C, it is for the harder version: we need to handle '1' in the cycle.

510A - Fox And Snake

There are 2 different ways to solve this kind of task:

First one is to simulate the movement of the snake head, and you draw '#'s on the board. The code will look like:

head = (1, 1)
repeat:
	repeat m-1 times: head move to right
	repeat 2 times: head move down
	repeat 2 times: head move down
	repeat m-1 times: head move to left
	repeat 2 times: head move down
	repeat 2 times: head move down
until head is out of the board

Another way is to do some observation about the result, you can find this pattern:

(4k+1) / (4k+3) line: "#######"
(4k+2) line: ".......#"
(4k+0) line: "#......."

510B - Fox And Two Dots

This task is essentially ask if there is a cycle in an undirected graph: treat each cell as a node, and add an edge if two cells are neighborhood and have some color.

There are lots of ways to do this, for example:

  1. Run dfs / bfs, if an edge lead you to a visited node, then there must be a cycle.

  2. For each connected component, test if |#edges| = |#nodes| - 1, if not then there must be a cycle.

510C - Fox And Names / 512A - Fox And Names

Let's first think about what S < T can tell us: suppose S = abcxyz and T = abcuv. Then we know that S < T if and only if x < u by the definition.

So we can transform the conditions name1 < name2, name2 < name3 ... into the order of letters.

Then the question become: do we have a permutation that satisfy those conditions. It is actually the classic topological order question.

One trick in this task is that, if we have something like xy < x then there is no solution. This is not covered in pretests. :)

510D - Fox And Jumping / 512B - Fox And Jumping

This task equals to: what is the minimal sum of costs that we can select k cards, so their GCD is 1.

First observation is that: GCD(x1, x2, ..., xk) = 1 means that for any prime p, there exist i such that xi is not dividable by p. So we only care about what prime factors a number contain. (So for example, 12 -> {2, 3}, 6 -> {2, 3}, 9 -> {3]})

The second observation is: If x ≤ 109 then it has at most 9 prime factors.

So after we select one number, we only care about these 9 or less primes. Then this problem equals to set covering problem (SCP), it can be done by mask DP. It can run in about O(2^9 * n^2).

510E - Fox And Dinner / 512C - Fox And Dinner

First finding is: if a + b is a prime, then one of them is an odd number, another is an even number. (that's why we set 2 ≤ xi)

Then we could find: every odd number have exactly 2 even number as neighborhood, and every even number have exactly 2 odd number as neighborhood. And that means we need |#even| = |#odd| to have a solution.

So it looks like bipartite graph matching, but every element matched 2 elements. And in fact it can be handled by maxflow: For each odd number, we add a node on the left side and link it from source with capacity equals to 2, and for each even number, we add a node on the right side and link it to sink with capacity equals to 2. And if sum of two numbers is a prime number, we link them with capacity equals to 1.

Then we solve the max flow, it have solution if and only if maxflow = 2 * |#even|.

We can construct the answer(cycles) from the matches.

Note: Actually this task is still solvable if we allow ai = 1. But you need some clever way to deal with it. We think it is too hard so we removed this case. What do you think about this decision?

512D - Fox And Travelling

We could find that some nodes cannot be visited. And more specific, if one node is in a cycle then it cannot be visited. So what about the structure of nodes that we can visit?

Let's first find a way to get all nodes that could be visited. We can deal with this by something like biconnected decomposition, but that is not easy to implement. In fact we can use this simple method: each time we pick one node that have at most 1 neighborhood and delete it. Repeat this process until we can't do it anymore.

We could find these nodes are actually belonging to these 2 kinds: 1. A tree. 2. Rooted tree. (that means, the root is attached to a cycle)

The rooted tree case is simple: we can solve it by tree DP. The state will be dp[i][j] = the way to remove j nodes in the subtree rooted at i.

Then how to solve the unrooted tree case? The way to deal with that is to transform it into rooted case. We have 2 solution:

  1. We select one unvisited node as the root by some rules: for example, we select one with minimal index. Then we just need to modify the DP a bit to adjust this additional condition.

  2. We could find if the tree has n nodes and we visit k nodes in the end, then there will be max(1, n-k) ways to choose the root. That means if we choose every node as the root and sum up them, we will count this case exactly max(1, n-k) times. So we just do the rooted DP for from node n times, and divide max(1, n-k) for ans[k].

The overall complicity is O(n4), and it can be optimize into O(n3) if you like.

512E - Fox And Polygon

Triangulation of polygon is something hard to think about. So the first key observation is that, we can transform this task into operations on rooted trees!

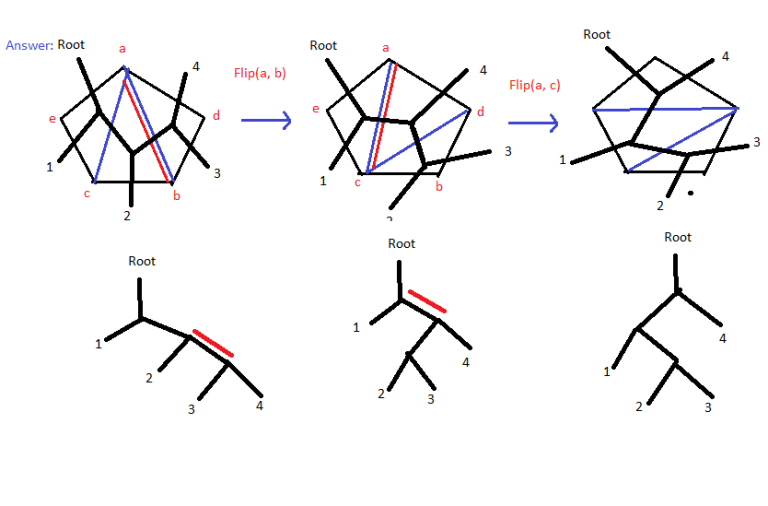
One Triangulation of polygon can be mapping to one rooted tree. And the flip operation can be mapping to the rotation of trees. (It is the operation we used to balance our BST) You can find the mapping from above picture. The red lines indicate the edge that will be flipped and the nodes we rotated.

Then we should find a standard shape of the tree, and solve this task: how to rotate any tree into this standard shape?

My solution is to choose the balanced tree as standard shape. The way to do that is this: find the node that the index is the middle number, rotate it to the top(that what we did for splay tree), and do the same thing for each subtree.

It is easy to see it could work in O(nlogn) steps.

  • Vote: I like it
  • +156
  • Vote: I do not like it

Comments Comments (70)
| Write comment?
»
10 years ago, # |
← Rev. 4   Vote: I like it +144 Vote: I do not like it

There is much easier solution for problem E. Let's convert any triangulation to triangulation where all diagonals go from first vertex. Suppose there are 2 adjancted edges (including sides) going from first that are going to not adjancted vertices, say f and t. Then there is diagonal from f to t. We can replace this edge with edge going from 1 to something. On each step we add one new edge going from 1, so in at most N - 3 steps we will have our base triangulation

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +17 Vote: I do not like it

    ...and running this on both the initial triangulation and the target traingulation can solve the problem: print the steps for [initial -> base] in order and the steps for [target -> base] in reverse order to get [initial -> base -> target] in at most 2N - 6 steps, which will always be at most 1994.

    → Reply
»
10 years ago, # |
  Vote: I like it +67 Vote: I do not like it

Div1 B can be solved with map, that stores all posibles GCD.

→ Reply
»
10 years ago, # |
  Vote: I like it +31 Vote: I do not like it

I solve C in a strange way... I find that the answer can be divide into two different perfect matches (with no common edge) of the bipartite graph. So I find the first perfact match of the graph, then delete the edge in the first match, then find the second perfact match. After that I can get answer from edges of the two matches. It gets accepted. But I don't know why. I can't prove it is right and I still think there maybe some cases can make it wrong (I haven't find yet). 9690671

→ Reply
»
10 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Actually, I implemented a much simpler solution for Problem B. I did a Dijkstra-like algorithm that stores the minimum cost of arriving at a certain GCD by using maps to store the costs.

Suppose we're on node g with cost c and we want to use coupon i, then the destination node would be gcd(g, Li) and the future cost would be c + Ci. The answer will be the cost of getting to node 1, and in case there's no path to node 1, then it's impossible.

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    I just solved this problem after a little help, and I don't even know how . this is my code. But I am confused how the inner loop is working. Since I am adding(in some cases) a new element to the map while iterating, how is it not TLEing? Does iteration on map create a copy of the map which it then iterates? Besides, when I am doing this adding separately , and then joining the two maps in the end, it gives wrong answer!

    → Reply
»
10 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Is there anyone can explain me a little bit more about the details of the solution to problem Div1-B, or is there any related code for it? Thank you guys!

I solved it by the naive DP method (unfortunately I did the initial part wrong during the contest), but the solution mentioned in the editorial is interesting.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +20 Vote: I do not like it

    Here is my code: http://ideone.com/bxjvtX

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thank you!

      → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 7   Vote: I like it 0 Vote: I do not like it

      I got the iterative approach! :D Thanks anyways :P

      9705405


      s = primes.size();

for(int mask = 0; mask < (1<<s); mask++){
	dp[mask] = INF;
}
		
dp[m[i]] = c[i];
		
for(int mask = 0; mask < (1<<s); mask++){
	for(int j = 0; j < n; j++){
		if(dp[mask] != INF)
			dp[mask | m[j]] = min(dp[mask | m[j]], dp[mask] + c[j]);
	}
}

ans = min(ans, dp[(1<<s) - 1]);
      → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Why can we get any number having the set of numbers which gcd of all numbers is 1?

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 3   Vote: I like it 0 Vote: I do not like it

        If you have two numbers a and b such that xa + yb = 1, with x and y being integers, then you can move to any point of the integer line.

        There is a very interesting lemma which states that what I said above is possible if a and b are coprime:

        Bézout's identity

        → Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    I

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Aaah, feels good to be blue again ;)

→ Reply
»
10 years ago, # |
  Vote: I like it +21 Vote: I do not like it

I'm glad that you didn't include the case a_i = 1 for div1C. It is a tricky case to deal with, and the problem is much cleaner without it.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +43 Vote: I do not like it

    Thanks for your feedback!

    I'll try to avoid tricky cases in the future!

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Div.2 B has simple and not too slow solution: delete all the letters which has less than 2 same neighbors (O(N*M)^2 ?), if any is left — there must be a cycle.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Does it work for this input:

    3 3
BAB
AAA
BAB
    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Em... Ou yes, it works: the central letter A will be deleted after some iterations, not immediately, but when the number of it's neighbors will decrease enough (example code: 9692376).

      → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In div 1. E, can't you find the root of the second tree, splay it to the root and recursively solve left and right subtrees? It's the same idea but without transforming to a canonical shape as you say and the complexity is still O(n lg n).

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    How can you guarantee that the second tree has a depth of O(lgn)? It could be a chain also.

    → Reply
»
10 years ago, # |
  Vote: I like it +34 Vote: I do not like it

"Note: Actually this task is still solvable if we allow ai = 1. But you need some clever way to deal with it. We think it is too hard so we removed this case. What do you think about this decision?"

Great decison! I don't like dealing with special cases when I already worked out the main idea.

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I wanna ask something, is there any possibility that the output of my IDE (I use Codeblocks) is different from the online judge?, here is the screenshot(using the same code but the output is different) here is the link of the screenshot :Screenshot

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Yes there is a possibility, as Codeblocks that you are using as an IDE use MingGW as its compiler and in Codeforces the compilation is done through g++/gcc compilers. And Codeblocks presumes many things, like if you use #include<Stdio.h> in codeblocks, it will run the program without giving any error, which is not so in g++/gcc compilers. Similarly, codeblocks doesn't handle the cases of overflows correctly. So its better to use ideone if you use Windows machine, or you switch to a linux machine. :)

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I solved Div1.B by just searching the answer. At first I got TLE, but when I removed some elements that will never be choosed, I got AC. It is hard to estimate the time complexity but it works :). My solution: 9694518

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    your solution seems interesting!! can you explain your solution a little bit ??

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Is it always the case that in lexicographical ordering, shorter words come before longer ones assuming all else is equal? The div1a example "xy < x equals no solution" seems to imply so, but I couldn't find any sources stating that this is always the case, so I was wondering if it's possible for the empty space to be lexicographically larger than any letters, or if anyone has a source saying otherwise?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    From the problem statement:

    Lexicographical order is defined in following way. When we compare s and t, first we find the leftmost position with differing characters: si ≠ ti. If there is no such position (i. e. s is a prefix of t or vice versa) the shortest string is less. Otherwise, we compare characters si and ti according to their order in alphabet.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Reading the problem statement — the secret to staying in division 1 :)

      Thanks!

      → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anybody explain how to solve 512B - Fox And Jumping by mask DP?

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

What's test 12 for 512A - Fox And Names?! I can't see full test. It's a huge test and shows "..."!
I try all of the special test cases mentioned in this post but my code still shows "Impossible" instead of "abcdefghijklmnopqrstuvwxyz" (the answer for the test 12).
Here's my submission: 9688819

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Your code gives "Imposible" in this case: 3 a ba bb If there are multiple edges from 'a' to 'b', your code will add indeg['b'-'a'] more than 1, but minus only 1 when checking edges from 'a' to 'b'.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      OMG! Thanks for your answer and great test case!

      → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For problem C, my solution is just using the binary-match. Use the Hungarian Algorithm, and add an additional condition: match[cur] != i, to restrict two points be circle. Like this: http://codeforces.net/contest/512/submission/9708200

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it +8 Vote: I do not like it

The solution for Div1. D is not clear for me. I get the idea of finding all vertices that can never be reached, and then making trees and rooted trees, however I can't seem to get how do we compute the dp[i][j], even only for rooted trees. Could some kind soul help me on that?

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 3   Vote: I like it +13 Vote: I do not like it

    Let's suppose we had a rooted tree. Suppose {w_i} is the set of children of i. Then the recurrence is

    where all the k_i are greater than or equal to 0. As a base case dp[i][j] = 0 if j is bigger than the size of the subtree rooted at i, and dp[i][0] = 1.

    To actually write this in code, let define an intermediate dp2[i][j][k], meaning we're computing dp[i][j], but we've already computed k of the children. Then,

    with some appropriate base case once k is equal to the number of children.

    Actually, my implementation was quite messy, so maybe there's a cleaner way to do this, though this is the basic idea.

    EDIT: Actually, there's also a special case when j=size of subtree of i, in this case, it's the number of topological sorts of the tree. I did this as a special case, though the idea is the same.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 2   Vote: I like it +8 Vote: I do not like it

      "EDIT: Actually, there's also a special case when j=size of subtree of i, in this case, it's the number of topological sorts of the tree. I did this as a special case, though the idea is the same." - dp[i][sz[i]] = dp[i][sz[i] - 1]

      :))

      → Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 3   Vote: I like it +29 Vote: I do not like it

    Lewin already gives a detailed explaination.

    Here is my code: http://ideone.com/zHeV5h

    See the dfs function for the calculation. It is not that complicated:

    dpValue dfs(int cur, int from)
{
	dpValue ret;
	ret.x[0] = 1;
	for(int i = 0; i < e[cur].size(); i++)
	{
		int t = e[cur][i];
		if(t == from) continue;
		ret = combine(ret, dfs(t, cur));
	}
	for(int i = 0; i < MAXN; i++)
		if(ret.x[i] == 0)
		{
			ret.x[i] = ret.x[i-1];
			break;
		}
	return ret;
}

    where:

    dpValue combine(dpValue A, dpValue B)
{
	dpValue ret;
	for(int i = 0; i < MAXN; i++)
		for(int j = 0; i+j < MAXN; j++)
		{
			ret.x[i+j] += ((A.x[i] * B.x[j]) % mod) * C(i+j, i);
			ret.x[i+j] %= mod;
		}
	return ret;
}
    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can Div1 C be solved without maxflow, using Kuhn's algotithm? I tried to split each number into two vertices, but had problems with a table with 2 foxes. Is it impossible and how can it be proved?

→ Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

>>Triangulation of polygon is something hard to think about. So the first key observation is that, we can transform this task into operations on rooted trees!

Lol nope, for this case triangulations are much simpler

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    Haha you are right.

    When I saw your solution passed all test cases within 2000 operations I know there are much more simple way to solve this task than I thought. :P

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone please explain me what is written in tutorial for DIV 1-B.i get that we have to find minimum cost subset with gcd=1.But,i am unable to understand the next few lines in the tutorial about prime numbers.help!!

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    An example: suppose you choose a 12, then you know for other numbers: there must a number that can not be dividable by 2 (otherwise the gcd will be dividable by 2), and there must a number that can not be dividable by 3 (otherwise the gcd will be dividable by 3) -- what's more, if we meet these 2 conditions, then gcd must be 1.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      "So after we select one number, we only care about these 9 or less primes. Then this problem equals to set covering problem (SCP), it can be done by mask DP. It can run in about O(2^9 * n^2)." Can you explain this part, please?

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Still the example above, if you select 12, then state will be: dp[do we have a number which can not be dividable by 2][do we have a number which can not be dividable by 3], this is 22, we have at most 9 prime factors, so we have at most 29 states.

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
          ← Rev. 3   Vote: I like it 0 Vote: I do not like it

          Why we can select one number? What happens if we chose not optimal number?

          For example 

          4
2 4 5 7
1 1 1 1000000000

          We select 7, and have one prime number: 7...

          → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Maybe it is a bit late, but I guess this is still helpful: here are the reference solutions for this contest:

  1. Div2-A: http://ideone.com/JP1Ksj
  2. DIv2-B: http://ideone.com/udz3bN
  3. Div2-C / Div1-A: http://ideone.com/KVobNb
  4. Div2-D / Div1-B: http://ideone.com/7MQqOm
  5. Div2-E / Div1-C: http://ideone.com/z3FsU2
  6. Div1-D: http://ideone.com/Y7j21a
  7. Div1-E: http://ideone.com/Orbacp

Note that for Div2-E / Div1-C, it is for the harder version: we need to handle '1' in the cycle.

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Sorry for bad English.

I found that the test case not strong enough.

My Solution : http://codeforces.net/contest/510/submission/10173150 get accepted even though it's wrong for this test case. 5 ab bc cd db ba

I hoping for test case update, thank you.

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

For Div1 C. is there any solution without using maximum flow?

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anyone tell me what is wrong in my solution http://codeforces.net/contest/510/submission/19968471 for Fox And Names.

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

May you please explain this part of solution for D?

Spoiler

Why in worst case there is only 9 prime factors??!

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I think harder version for Div1C can be solved via Hopcroft-Karp bipartite matching.

Nodes in the bipartite graph will be formed from the given numbers-if two indices x and y, a[x] + a[y] is a prime, then node (x, y) will exist.

Thus, we have pairs (xi, yi) on both sides of bipartite graph. Create edge between pair p on left side and pair q on right side if a[p.second] + a[q.first] is a prime and p.second != q.first.

Run Hopcroft-Karp algorithm on this new graph, and we can find answer from this.

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In div1 B, can somebody please explain to me why does the naive DP of f(i, gcd) isn't giving TLE? How to prove that total number of gcd will not exceed the limit?

→ Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

div2C code doesn't give valid output for such inputs

2
abc
abc
→ Reply