Закончилась четвертая личная интернет-олимпиада.
Здесь предлагается поделиться впечатлениями.

Задачи
Результаты
Тесты и решения жюри (41 мб)
Генераторы тестов и решения жюри

Краткий разбор

А. Муравьи-мутанты
Будем для каждой ловушки слева направо искать муравья, который в нее попадёт. Для первой это будет самый правый муравей, начинающий слева от нее, для второй — самый правый из всех начинающих слева от нее, кроме того одного, который уже словушился, для третьей... Идея понятна, для эффективной реализации достаточно было пройти ловушки постепенно кидая муравьев в стек.

В. Разбиение на камеры
Нельзя, когда n < k, k = 1 или n нечётное, а также если k нечётное и n = k или n = k + 1.
Возможное решение: можно на первые две позиции поставить 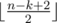и 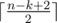а на все остальные — 1.
Поправьте меня, если я неправ.

С. Производство паутины
Несложная динамика. Пусть dp[i] — минимальная стоимость произвести на свет префикс длины i.
Понятно, что перед удалением нет смысла делать добавление символа. Тогда можно ограничиться двумя операциями: добавить символ (стоимость a) и добавить в конец какой-то префикс текущей строки (стоимость b + c·dellen, где dellen — это длина текущей строки минус длина добавляемого префикса).
Тогда dp[1] = a; dp[i] = min(dp[i - 1] + a, min_j(dp[j] + b + c·(j - (i - j)))), где j — все возможные длины префиксов, из которых мы можем получить текущий префикс нашей второй операцией.
Как же теперь определить все нужные j? Для этого стоит заметить что каждый j будет учитываться при пересчете какого-то количества подряд идущих dp[i], причём этот отрезок явно определяется Z-функцией от j. Также нелишним будет учесть, что в формуле пересчета dp[j] + b + c·2·j зависит только от j. а -c·i -- только от i.
Исходя из вышеупомянутого, используем алгоритм заметающей прямой: пусть мы храним множество всех отрезков для всех j, в которых мы сейчас находимся, и для каждого храним первое слагаемое, тогда пересчет очевиден. Поддерживать множество тоже несложно.

D. Эвакуация
Тоже несложная динамика. В этот раз на дереве.
Подвесим дерево. Пусть dp[v] — максимальный момент времени, в который мы можем начать бежать из вершины v вниз по дереву, чтобы спастись, если мы можем это сделать, и -1 иначе. Пересчет: dp[v] = max( - 1, max(min_u(dp[u], t_u) - l_u)), где u — дочерняя вершина, t_u и l_u — параметры ребра .
Решение на 40: ну подвесим дерево за все вершины по очереди и запустим такую штуку.
Решение на 100: применим стандартный приём для подсчета динамики на неподвешенном дереве. Подвесим за произвольную вершину и посчитаем динамику. Затем запустим DFS из корня и для каждой вершины, кроме него, представим, что ребро из нее в предка является как будто является ребром в новую дочернюю вершину, и пересчитаем dp[v] с учетом неё.
Но просто брать для этого пересчета dp[parent] нельзя, так как оно само уже посчитано с учетом (бывшего) dp[v]. Поэтому каждый раз при переходе от parent к v мы передаем параметр up, который показывает, каким бы было dp[parent], если не существовало v. Как найти up? Оно очевидным образом получается из максимального из значении динамики всех дочерних вершин parent, кроме v (а еще и up, который для parent), а чтобы считать его для всех v, надо еще поддерживать два максимальных таких значения.
Для лучшего понимания можно посмотреть мой код.
Судя по всему, решения жюри в архиве основаны на другой идее (сливаемых-переливаемых множеств).