pranay2063's blog

Inverse modulo of a range of numbers modulo m
By pranay2063, 10 years ago, In English

Hi all,

While searching about inverse modulo, i got to know about a concise algorithm to find inverse modulo of numbers in range[1...n) under modulo m.

Time complexity of this approach is O(n).

Implementation of the algorithm:

r[1] = 1; for (int i=2; i<n; ++i) r[i] = (m — (m/i) * r[m%i] % m) % m;

Here is the link: http://e-maxx.ru/algo/reverse_element

I am unable to understand the proof of the algorithm. It would be very helpful if anyone explains the same in a simple way.

  • Vote: I like it
  • +3
  • Vote: I do not like it

»
10 years ago, # |
← Rev. 3   Vote: I like it +1 Vote: I do not like it

m mod i = m — m/i*i
m mod i = — m/i*i (mod m)
// multiply by r[i]
r[i] * (m mod i) = — m/i*i *r[i] (mod m)
r[i] * (m mod i) = — m/i (mod m)
// multiply by r[m % i] — reverse to (m mod i) (reverse modulo m)
r[i] = — m/i * r[m % i] (mod m)

→ Reply
»
10 years ago, # |
  Vote: I like it +1 Vote: I do not like it

This is the simplest I can think of:

We want to prove that .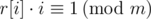

Now multiply both sides by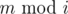 . We assume that 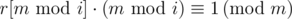already.

And note that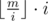 is the largest multiple of i that is not greater than m. In other words, .

Thus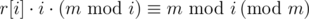 , and so 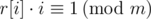. That is, r[i] is the modular inverse of i modulo m.

There are some massive holes (mathematically) there, but should be easily patched up; but you want a simple explanation, not a completely correct one.

→ Reply
»
7 years ago, # |
  Vote: I like it +11 Vote: I do not like it

I was discussing with mgold earlier about another way to find the modular inverse of the first N numbers mod a prime number P.

Find the factorial of the first N numbers, let's say fak[n] = n!, 

fak[0] = 1
for k=1...N:
    fak[k] = fak[k-1] * k % P

Find the modular inverse of N!. This is a result of Fermat Little Theorem and it can be computed in O(logP)

ifak[N] = modpow(fak[N], P - 2)

Now we can calculate the inverse of each factorial backwards in O(N).

for k=N-1...0:
  ifak[k] = ifak[k+1] * (k+1) % P

Most of the times I need to pre calculate the inverse of each of the first N numbers just to calculate the inverse of the factorial. So I can get C(n,k) in O(1). In that case we are done.

But If you actually need the inverse of the first N numbers you can compute them:

for k=1...N:
    inv[k] = ifak[k] * fak[k-1] % P

Here is my code using this method: 35525761

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    Can you explain how the ifak[k] = ifak[k+1]*(k+1)%P works? More specifically, how modpow(fak[N],P-2) and ifak[k+1]*(k+1)%P produce the same result?

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      Can you explain how the ifak[k] = ifak[k+1]*(k+1)%P works?

      Notice that the inverse of factorials is computed in reverse order. You start by correctly computing the inverse factorial of $$$n$$$ which is $$$n!^{p - 2} mod(p)$$$: ifak[n] = modpow(fak[n], p - 2)

      Now that we now the inverse of $$$n!$$$ we can deduce smaller inverse in a similar fashion as we compute the factorials themselves

      $$$(k + 1)!^{-1} = (k! \cdot (k + 1))^{-1}$$$
      $$$(k + 1)!^{-1} = k!^{-1} \cdot (k + 1)^{-1}$$$
      $$$(k + 1)!^{-1} \cdot (k + 1) = k!^{-1}$$$

      So we deduce $$$k!^{-1}$$$ from $$$(k+1)!^{-1}$$$ easily using: ifak[k] = ifak[k + 1] * (k + 1) % p.

      More specifically, how modpow(fak[N],P-2) and ifak[k+1]*(k+1)%P produce the same result?

      Not sure what do you mean by this.

      • modpow(fak[N],P-2) is only used to compute the inverse of $$$N!$$$.
      • The recurrence ifak[k+1]*(k+1)%P is used to compute the remaining factorial inverses. $$$0 \le k \lt N$$$
      → Reply
      • »
        »
        »
        »
        5 years ago, # ^ |
          Vote: I like it +10 Vote: I do not like it

        What I meant earlier is that we could calculate inverse of each x! for x from 0 to N separately using modpow(fak[x],P-2) or we could do it faster with the iterative version, and I wanted to know how using both of them would give the same result.

        With the proof for the iterative step, it is very clear now, Thank you for this wonderful explanation!

        → Reply