I've participate in Div.2 contest and enjoyed many of the problems. Let start discussions about problems?
How did you solve N, O?
Upsolving is ON.
Next: 12. 29.03.2015 11:00 Grand Prix of America
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
I've participate in Div.2 contest and enjoyed many of the problems. Let start discussions about problems?
How did you solve N, O?
Upsolving is ON.
Next: 12. 29.03.2015 11:00 Grand Prix of America
| Название |
|---|



Как решать С и К?
В С у меня динамика за O(N^4). На плюсах упихалась.
Давайте взглянем на грань, содержащую ребро 1-n, и будем ее строить по порядку: 1-a1-a2-...-n. Тогда на каждом ребре 1-a1, a1-a2, ..., у нас торчит по многоугольнику с меньшим числом вершин и треугольников, соответственно будем использовать динамику. Будем считать динамикой две вещи: ответ в задаче для (n, k), и количество "частично построенных" граней — цепочек 1-a2-...-at, с добавленным многоугольником на каждом ребре, суммарно содержащих n вершин и k треугольников. Ну и нужно аккуратно учесть, что свежепостроенная грань 1-a1-n может оказаться треугольником тоже. Получается O(N^2) состояний и переходы тоже за O(N^2).
У нас что-то похожее и тоже сдали за O(n^4), но там легко можно свести пересчет к перемножению многочленов и улучшить асимптотику.
Но как? Фурье же не помогает умножать многочлены по модулю 10**9+9?
Карацуба?
Ну либо Карацуба, либо две Фурьешки. Что именно будет тут быстрее не берусь судить, но скорее всего Карацуба, эффективный размер многочленов там порядка 100.
А как через две Фурьешки?
Одну обычную, чтобы примерно понять, какие числа, вторую по модулю, чтобы уточнить значения. Числа в произведении порядка 10^20 (поэтому одного ффт в инт128 не хватает), но модуля порядка 10^9 должно хватать, чтобы уточнить (а если бы не хватало можно было бы влезть в инт128)
Понял, спасибо! Написал, и на (300, 150) даже работает правильно, но в несколько раз медленнее выходит, чем с тупым умножением многочленов :( На Карацубу больше надежды, наверное.
Решение для K (на контесте не сдали, но зашло в дорешке).
Идея 1. Пусть k (число апельсинов в английской постановке, которые мы делим) большое. Тогда дележ в зависимости от n будет выглядеть так:
1) n = 1 -- всё берет первый, результат (k)
2) n = 2 -- всё берет первый, результат (k, 0)
3) n = 3 -- результат (k — 1, 0, 1). Тут первому надо кого-то подкупить, и это может быть только третий.
4) n = 4 -- результат (k -1 , 0, 1, 0).
5) n = 5 -- результат (k — 2, 0, 1, 0, 1). И так далее.
Идея 2: а что же происходит, если k не очень большое, то есть на каком-то этапе у первого при дележе остаётся ноль? Если число человек нечётное, то ситуация однозначная -- первый хочет не уйти в минус, поэтому себе оставит ноль но подкупит остальных. Если число человек чётное, то он не может купить всех прошлых нулей но может купить часть. Поэтому тут у некоторых появится вывод в ответ min = 0, max = 1.
Идея 3: Что происходит дальше при росте числе участников, то есть когда один человек не может купить себе победу? Мотивирующий пример: очень много человек и 2 апельсина. Тогда разумно проголосовать за почти последнего чтобы хотя бы остаться.
Как это формализовать: проще всего понять на частном случае k = 1. Тогда если человек 5, то первый никак не останется. Но если человек 6, то пятый гарантированно поддержит шестого, и тому надо лишь одного человека подкупать. Итого, с 6 всё хорошо. Далее получается похожая ситуация, и до 10 плохо, а с 10 хорошо. Размеры таких групп растут как +2, +4, +8, ..., то есть таких будет логарифм. Раздача апельсинов: не влезли в группу (то есть за ней) -- (-1, -1), Влезли: (0, 0). До группы (1, 0).
Код с AC: http://paste.ubuntu.com/10608540/
С. Пусть f(n, k, s) — количество разбиений n-угольника на k треугольников, при этом из вершины s в вершину с бОльшим номером проводится разрез, отсекающий часть, которая больше не разрезается и при этом нет разрезов, проходящих через вершины, номера которых больше s. Состояния такой динамики просчитываются за квадрат, что даёт решение О(n5). Но можно заметить, что при расчёте переходов мы просто суммируем значения f для некоторого фиксированного k, а первый и третий параметр просто принимают значения из некоторого прямоугольника. Это позволяет, рассчитав частичные суммы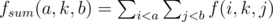 , считать сумму на любом прямоугольнике за О(1) и, соответсвенно улучшить предыдущую оценку до О(n3).
, считать сумму на любом прямоугольнике за О(1) и, соответсвенно улучшить предыдущую оценку до О(n3).
Кроме того, имеется ещё такое решение за квадрат, но как его получить самому — совершенно непонятно.
Как решать F div1?
Ну там нужно найти минимальное число, у которого ровно n нечетных делителей.
Как только дошли до этого, дальше пишем перебор. Сравнить два числа можно, взяв логарифм, так как у нас есть их факторизация.
А как доказать, что именно минимальное число у которого ровно n нечетных делителей будет ответом?
что значит, что k представляется как какая-то сумма?
$2k = (b - a)(b + a + 1)
То есть нам нужно представить 2k как произведение двух чисел разной четности(вроде можно понять, что любое такое разбиение задает какие-то a,b, но 2-ка входит ровно в один из множителей, значит добавление в k двоек не добавляет нам новых способов. Кол-во способов так разбить и есть кол-во делителей.
Примерно так.
Ок, давайте поподробнее. Фактически, надо найти наименьшее нечётное число с ровно n делителями.
Пусть p0 = 2, p1 = 3, p2 = 5, .... Тогда, как известно у числа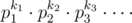 ровно (k1 + 1)·(k2 + 1)·(k3 + 1)·... делителей. Тогда для наименьшего числа, у которого ровно n делителей k1 ≤ k2 ≤ k3 ≤ .... То есть, все ненулевые ki идут в начале. Если k20 > 0, то у числа не меньше (1 + 1)20 > 105 делителей. То есть, в разложении интересующего нас числа входят лишь простые от p1 до p19. Скажем, что pi имеет номер i. Пусть также
ровно (k1 + 1)·(k2 + 1)·(k3 + 1)·... делителей. Тогда для наименьшего числа, у которого ровно n делителей k1 ≤ k2 ≤ k3 ≤ .... То есть, все ненулевые ki идут в начале. Если k20 > 0, то у числа не меньше (1 + 1)20 > 105 делителей. То есть, в разложении интересующего нас числа входят лишь простые от p1 до p19. Скажем, что pi имеет номер i. Пусть также
bound = 19.Пусть теперь . Теперь у нас есть
. Теперь у нас есть
dp[num][k]— наименьшее число, имеющее ровно k делителей и использующее в своём разложении простые с номерами отnumдоbound. Изначально посчитаемdp[bound][k]— это простоdp[num][k], мы хотим его вычислить. Переберём, в какой степени pnum войдёт в ответ. Тогда если эта степень d (очевидно, k делится на d + 1), то нужно сравнить текущее значениеdp[num][k]сdp[num + 1][k / (d + 1)] * (p_num)^kи, если надо, обновиться.Ответ будет лежать в
dp[1][n]. Асимпотика no(1), если перебирать только делители n, но в любом случае не должно получать TL, по идее.Как хранить
dp[num][k]? Будем хранить остаток по модулю 109 + 9 и long double, содержащий ответ (для сравнения). Если будут проблемы с точностью, то можно дополнительно хранить остаток по модулю 264, чтобы сравнивать подозрительно близкие числа.Код..
P. S. HTML-рендерер странно обрабатывает верхние и нижние индексы, приходится добавлять пустой фантомный объект, чтобы нормально работало.
P. P. S. А также интерпретирует
\pmodкак\pm od.А можно просто в длинке хранить.
А еще можно прологарифмировать и сумму логарифмов хранить.
Только тут гораздо менее очевидно, что ответ найдется корректный
Кстати, насколько близкие между собой могут быть значения для различных вариантов? Проблемы с точностью вообще могут возникнуть, у кого-то есть какие то плохие тесты, или же там всегда все хорошо и можно доказать, что какого-нибудь логарифмирования гарантированно хватает?
Я проверял все ответы, удовлетворяющие ограничениям — логарифмов хватало.
Расскажите пожалуйста G и L?
G — Не читал.
L — просто переберем какого парня и куда мы хотим переместить. Быстро отвечать на измененный мир можно, храня мапку для количества и сет для максимума.
Вопрос снят))
Если ноль, то не надо пытаться с этой дорожки никого перекидывать, может проблема в этом.
G: Переведём все показания в секунды. Очевидно (в силу кусочной линейности целевой функции), что минимум достигается, когда все часы привели к какому-то из исходных показаний. Отсортируем показания, посчитаем префиксные и суффиксные суммы, после этого уже не сложно считать ответ при фиксированном финальном значении за O(1). Итого .
.
А как именно считать префиксные и суффиксные суммы?
Ещё раз, у нас есть набор чисел по какому-то модулю, нужно к каждому прибавит что-то и сделать все равными. Переберём финальное значение — x.
Тогда, если ai < x, то к ответу прибавим x - ai. Иначе к ответу прибавляется M - ai + x.
Если числа предварительно отсортировать, то ответ для x = ai можно подсчитать через сумму всех чисел, меньших ai (префикс) и всех больших.
На Л найдем из массива: 1) мах. значение дорожки, 2) число мах. значений, 3) число (мах. — 1) значений. Тогда едем по массиву, и приостанавливаемся толко на мах. дорожках. Проверяем соседние к мах. дорожки: можем ли туда скинуть плавца, и как тогда измениться количество несчастных. Надо описать все возможные сценарии. Например тут (3 3 3 1 4) из 5-ой дорожки в 4-ую плавца нескинем, так как много дорожек станут несчастными. А тут (4 3 3 1 4) можем скинуть.
Удивила P и что её так мало команд решило. Конкретно у меня с того момента как я узнал условие задачи (с того момента как мне его перевели, ибо я не знаю английский) ушло 24 минуты на решение. Всего 9 строчек кода: Код
O: ternary search.
Is it possible to solve O using golden section search or binary search?
Расскажите, пожалуйста, D и J.
J: факторизируем m и посчитаем для каждой степени простого отдельно, потом "сольём" по КТО. Пусть теперь m = pa,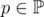 .
.
Тогда посчитаем отдельно степень p, входящую в цэшку (легко) и часть этой цэшки, взаимно простую с m. По модулю m мы умеем обращать за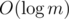 , так что надо лишь научиться быстро считать "факториал без p-шек" по модулю m (то есть каждое от 1 до n делят на p, пока оно делится, а результаты перемножают).
, так что надо лишь научиться быстро считать "факториал без p-шек" по модулю m (то есть каждое от 1 до n делят на p, пока оно делится, а результаты перемножают).
Но его можно посчитать, как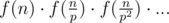 , где f(n) — произведение всех чисел от 1 до n включительно, взаимно простых с m, по модулю m. Так как m мало, то можно считать
, где f(n) — произведение всех чисел от 1 до n включительно, взаимно простых с m, по модулю m. Так как m мало, то можно считать 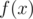 за
за 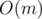 (будет по модулю m много одинаковых кусков и "хвост").
(будет по модулю m много одинаковых кусков и "хвост").
Можно подробности о слиянии?
В нашем случае (так как m ≤ 106) можно просто перебрать остаток по модулю m из условия и проверить, удовлетворяет ли он полученным сравнениям (по КТО такой остаток есть и ровно один) с break-ами. Сложность O(m), так как не более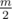 остатков переживут первое сравнение, не более
остатков переживут первое сравнение, не более 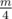 второе и так далее.
второе и так далее.
Код в правке 5.
При более высоких ограничениях можно было бы уменьшать количество сравнений, превращая два сравнения по модулям n, m (gcd(n, m) = 1) в сравнение по модулю mn (m в этом комментарии не имеет отношения к условию).
Действительно, пусть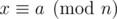 ,
, 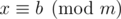 , где a ≠ b (случай a = b очевиден).
, где a ≠ b (случай a = b очевиден).
Тогда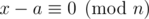 ,
, 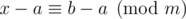 , то есть если k таково, что
, то есть если k таково, что 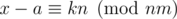 , то
, то 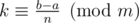 , откуда
, откуда 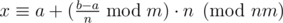 то есть мы вычислили x по модулю nm (а
то есть мы вычислили x по модулю nm (а 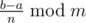 можно вычилить за
можно вычилить за 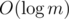 с помощью расширенного алгоритма Евклида).
с помощью расширенного алгоритма Евклида).
D:
Построим centroid decomposition of the tree (вроде так называется).
В каждой вершине храним
set(dist, time, color)-- значит, что умеем во времяtimeпокрывать вершины на расстоянииdistот текущей.Обновление: проходим по предкам вершины (их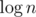 ) в декомпозиции и пихаем в
) в декомпозиции и пихаем в
set[par](d - distance(v, par), time, color).Запрос: также проходимся и узнаём, кто наиболее поздний покрыл вершину.
J:
Посчитаем для pk потом восстановим по КТО.
Для этого надо научиться представлять n! = py·x, где x не делится на p. Это делается также, как здесь, но по модулю pk.
D: О, эта штука как-то называется по умному, неожиданно.
а как в таком сете узнать
кто наиболее поздний покрыл вершину?На самом деле при добавлении
(d, t, c)нужно удалять все записи у которых записано расстояние меньшее, чемd.Теперь для каждого из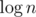 предков узнаем, когда этот предок покрыл вершину из запроса (это наименьший элемент в сете для
предков узнаем, когда этот предок покрыл вершину из запроса (это наименьший элемент в сете для
par, который не меньшеdist(par, v)) и возьмём того, кто покрыл позднее всех.D — зачетная задача! Спасибо, почему-то про центройд даже не думали :(
Я думал про центроид, но в сторону divide-and-conquer, а не структуры данных :(
Спасибо за D, наконец-то пошел и разобрался с этим разбиением.
А я правильно понимаю, что у авторов какое-то другое более медленное решение (это же за O(n * log(n)2)), так как TL аж 9 секунд?
У авторов решение такое же. Просто по каким-то необъяснимым причинам на нашем контестере решение работало в три с половиной раза медленней, чем на полигоне. Поскольку выяснилось это слишком поздно, разбираться с этим времени уже не было.
Возможно, не у авторов более медленное решение, а авторы допускают использование более медленных решений участниками)
У нас, например, N*sqrt(N)*log(N) — построили для дерева что-то вроде корневой декомпозиции, выбрав sqrt(N) вершин, которые разбивают дерево на блоки.
а I и H можно?
I:
Жадно пытаемся сделать xm как можно больше и т.д.
Можно увеличивать xm по единице для всех m > 2, для 1 и 2 бинпоиск (можно и для остальных бинпоиск, но могут быть проблемы со сравнением).
Как понять, что жадность работает: условие утверждает, что для любых входных данных ответ есть :)
H:
Пусть s < f.
Пусть s = 1, иначе обязательно нужно сначала сходить налево (иначе туда уже не попадём) и вернуться в s + 1 затратив 1 прыжок длины 1.
Аналогично f = n.
Теперь нужно пройти от границе к границе, это выгодно делать так: s -> s+2 -> s+1 -> s+3 и т.д.
А если мы прыгали сначала слева и f!=n, то мы должны допрыгать от s+1 до f-1?
Да, по аналогии:
Было 1 < s — теперь стартуем из s + 1,
Было f < n — теперь прыгаем до f - 1.
Как понять, что жадность работает: условие утверждает, что для любых входных данных ответ есть :)
"Решение всегда существет" != "жадник всегда найдет решение".
Ну да, но в данном случае, почти очевидно, что он работает, так как мы просто сводимся к задаче с меньшим m и выгодно сделать xm как можно более большим.
Более строго: рассмотрим жадник — пусть жадно выбрали xm и xm - 1 и оказалось, что xm ≤ xm - 1. Тогда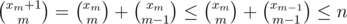 , то есть xm можно было взять больше. Противоречие.
, то есть xm можно было взять больше. Противоречие.
Даже получилось доказательство существования, поскольку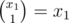 .
.
I: В моём первом решении, при
m < 7, при подсчете числа перестановок случалось переполнение. Случалось оно в выражении видаx * y / z. Произведениеx * yточно делится нацело наz, поэтому пришлось писать "умное" деление, когда перебираются все делителиzи либоx, либоyделятся на эти делители. Но это умное деление работало очень долго на тестеm = 2, поэтому для этого случая я отдельно написал подсчет числа перестановок, какx * (x + 1) / 2. И поправка:m >= 2по условию. Хотя на тестеm = 1можно сразу выводитьn, странно что решили сделать такие ограничения.Вместо умного деления можно разделить на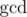 .
.
А чтобы вообще было безопасно, можно писать так:
Что-то я и не вспомнил про gcd... Хотя я еще и минут 20 думал как модернизировать решение, чтобы оно быстро работало при m=2, хотя это очевидно и просто... 4 часа контеста дают о себе знать.
А по Н ва4 никто не ловил? (Решено)
Yeah, help on O would be strongly appreciated. We tried binary search and golden section search, but somehow kept getting WA.
Можно B и C ещё? Как там считать динамику?
B:
dp[i][j][l], 0 <= i <= n/2, 0 <= j <= i, l = 0,1. сколько последовательностей с i открывающими, j — закрывающими, и если l = 0, то еще не было суммы k, иначе была.А когда будут настоящие результаты? А то слабо верится, что ITMO#1 решили 8, а Тапиры — 7 (при этом за первые 2 часа, а потом видимо ушли отдыхать)
Последнее обновление из Казани было на 2:48; с этого времени никаких апдейтов не приходило.
У нас 12, у Тапиров 10.
Спасибо за информацию; а где-нибудь можно посмотреть окончательный монитор онсайта? Пока ждем на синхронизацию с таблицей OpenCup)
O: что может быть плохого в 10 тесте?
Важно было искать ответ не на отрезке
(x1,y1) - (x2,y2), а на прямой заданной этими точками. То есть если решение — тернарный поиск, то нужно было расширить отрезок, на котором ищется решение. И есть два способа это сделать:Первый и более сложный способ — найти проекции всех точек на прямую (то есть опустить перпендикуляр) и взять самую маленькую и самую большую точку по
x(y). Ответ находится точно между этими точками.Второй способ: просто взять точки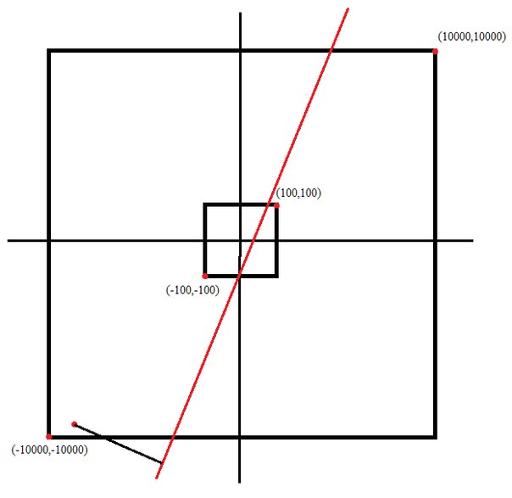
(-20000,yy1)и(20000,yy2)((xx1,-20000)и(xx2,20000)для вертикальной прямой) принадлежащие прямой. Но тут у вас может возникнуть вопрос: а зачем брать такие большеx, если ограничение на ввод10^4. Ответ прост: проекция точки на прямую может лежать за пределами прямоугольника ограничивающего ввод:Думаю где-то в этом тексте вы найдёте ответ на свой вопрос.
спасибо :)
Delete.
А как решали Q(Микросхемы) div2? Есть ли там формула или последовательность известная?
Я динамику написал:
i— количество точек,j— количество прямых,dp[i][j]— количество способов.Начальные состояния:
dp[i][0] = 1при любомi,dp[2][1] = 1.Допустим нам нужно провести
kпрямых. Теперь переберём стартовую точку и точку с котором мы будем её соединять (здесь подразумевается, что если мы берём за стартовую точкуz, то все точки меньшеzмы не с чем соединять не будем, иначе это приведёт к повторению способов). Соединив их у нас по обе стороны оказалось некоторое количество точек (за исключением тех, которые мы не с чем соединять не будем):xиy, и нам нужно провести на одну прямую меньше, а значит можно перебрать количество прямых, которое будет по одну сторону —l. И тогдаdp[i][j] += dp[x][l] * dp[y][k - 1 - l].Решение за O(n^5) (хотя на самом деле за O(n^3 * k^2) )
Код
Можно решать за четвёртую степень если зафиксировать один конец. При этом нужно не забыть прибавить количество разбиений в котором этот конец не участвует (
dp[i-1][j]).Код
P.S. У меня там пара кривых ифов. Уверен что их можно как-нибудь убрать.
How to solve problem E div 1? It seems that it is useful to try different rotations of source points with maybe some ternary search, but we did not get any further.
There is always an answer with at least one side parallel to some edge of the convex hull
в задаче N сказано что дистанции телепорта целые числа, но по моему наблюдению это не так.
Ко всем задачам делаются валидаторы, которые проверяют корректность входных данных. Только что посмотрел, валидатор к этой задаче проверяет, что все дистанции — целые числа.
Спасибо за ответ. Я понимаю что всё проверяется, но если можете проверять заявки 980 и 999, думаю ясно, что-то не так.
У меня на руках исходники только тех команды, которые приезжали в Казань. Если вы у нас не были, то я бессилен.
А у тебя есть доступ к тестам? Можно узнать ва4 по задаче Н?(Решено)
Next OC round in shedule have appeared: 12. 29.03.2015 11:00 Grand Prix of America
Спасибо авторам за интересный контест!
Дописывал Е около 4 часов, залил на Upsolving — уже 3 дня не могу преодолеть 2й тест, хотя все мои тесты проходит на "ура". Можно открыть 2й тест? (можно в ЛС)
Он с большими числами. Тест:
Ответ:
А вообще — скоро выложу контест в тренировки.
Спасибо! Оказалось, не знал особенностей cout при выводе дробных чисел :)
Выложил контест на тренировки. Первый и второй дивизион.
Спасибо.
Как решается O и N?
How to solve C, I don't no how to solve this problem in DP way