Heisenbug's blog

Binomial coefficients with constant "k"?
By Heisenbug, 10 years ago, In English

Is there a stupid trick to calculate n-choose-k for a range of n with k always the same, which is faster than forming the full Pascal's triangle? With some fixed k, I need to calculate all n-choose-k modulo 10^9+7 for n up to 100,000 but there's no way I can calculate all the coefficients within 3 seconds.

  • Vote: I like it
  • +3
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it -11 Vote: I do not like it

C(N, K) = N! / (K! * (N — K)!) => C(N + 1, K) = C(N, K) * (N + 1) / (N + 1 — K), that's obvious.

I think, you don't know how to perform the division, so please read about modular multiplicative inverse.

→ Reply
»
10 years ago, # |
  Vote: I like it +17 Vote: I do not like it

You can divide by x over a prime modulus M by multiplying by xM - 2. This lets you use factorial formula for n choose k.

→ Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Well, for that task you don't even need the fact that K is constant, if you precalculate all the factorials, you can answer the nCk query in logarithmic time.

→ Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Won't you answer the query in O(1) time then?

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      Nope, you will need to calculate modular inverse(O(logN)).

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Actually, you can calculate modular inverse O(1) with O(n) pre-calculate.

        Let rv[x] is the inverse of x under M, then rv[x] = rv[M % x] * (M — M / x) % M and of course rv[1] = 1.

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          That's awesome!! I'm eager to know why it works. Would you explain please?

          → Reply
          • »
            »
            »
            »
            »
            »
            10 years ago, # ^ |
              Vote: I like it +1 Vote: I do not like it

            let M = kx + r, r < x, then k = M / x, r = M % x and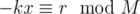

            both multiple rv[x] we will get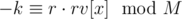

            so,

            → Reply