Problem A:
https://youtu.be/xIvFJYo9928?t=1h57m56s
Problem B:
https://youtu.be/xIvFJYo9928?t=5h43m9s
Problem C:
https://youtu.be/xIvFJYo9928?t=2h35m50s
Problem D:
https://youtu.be/xIvFJYo9928?t=2h58m55s
Problem E:
https://youtu.be/xIvFJYo9928?t=3h12m36s
Problem F:
https://youtu.be/xIvFJYo9928?t=4h1m56s
Problem G:
https://youtu.be/xIvFJYo9928?t=5h34m30s
Problem H:
https://youtu.be/xIvFJYo9928?t=4h17m29s
Problem I:
https://youtu.be/xIvFJYo9928?t=3h30m17s
Problem J:
https://youtu.be/xIvFJYo9928?t=4h31m59s
Problem K:
https://youtu.be/xIvFJYo9928?t=5h16m49s
Problem L:
https://youtu.be/xIvFJYo9928?t=3h41m51s
Problem M:
https://youtu.be/xIvFJYo9928?t=4h49m29s
--- Thanks to: SuprDewd ---
More solution sketches: http://www.csc.kth.se/~austrin/icpc/finals2015solutions.pdf
6-Hour Live Coding with SnapDragon where he goes through the WF problems: https://www.youtube.com/watch?v=fFs8-cTq83k










Problem A:
Ad hoc.
Problem F:
Use multiple Dijkstra's algorithms for every letter of text. As a starting vertex for ith iteration use fields with text[i - 1] and computed distance. For first iteration starting point is at (0, 0) and distance 0.
F had a rather strict time limit and some (not all) solutions that used Dijkstra got TLE.
F can actually be nicely implemented as a single breadth-first search.
My Dijkstra's solution passed time limits with 2s. reserve. Can you elaborate on that?
Yes, I didn't take part in the Finals, but I solved Problem F using BFS.
I don't know about exact solutions but in yesterday's live streaming, some analysis and solution approach was given in between the telecast.
Youtube link
Hope this helps...
Thank you! I've added links to all problems.
As an extension, If someone can clip these analysis snippets and upload them seperately !!
AFAIK, this will quite probably be done in the near future by the official ICPC channel. And if it isn't, we still have the sources of those recordings somewhere :)
Problem C went straight over my head. I have no clue why the construction in the video is working :/ I am familiar with the basic maximum-flow problem (as given in CLRS) but don't know how minimum cost is playing it's role here.
Here is what I understood, a unit flow into a vertex means that one catering team is serving an event and in addition to a capacity, each edge has been given a cost per unit flow. Now,
Could someone please give a more detailed explanation? I don't find the problem to be trivial :/
Here's how I solved it:
build a suitable weighted bipartite graph
incrementally, for each x, find the value M[x] of the cheapest matching with exactly x edges (by always applying the cheapest augmenting path)
the smallest of the values M[N-K] through M[N-1] gives you the solution
First, imagine you want to use exactly N teams. The cost is obvious: it's the sum of all distances start-location (i.e., the sum of the second row of the input file). This will be called the basic solution.
Now, imagine you want to use exactly F teams fewer (i.e., use exactly N-F teams). What is the cheapest way to do it?
Well, exactly F times we need to send a team from some party location to some other party location. Compared to the basic solution, how much will we save if we send a team from party X to party Y? That's easy: We have to pay the cost from X to Y, but not the cost from headquarters to Y, so we save the difference of those two.
Now, imagine a bipartite graph where each partition has N vertices (one for each party). For each X < Y there will be an edge from vertex X in the left partition to vertex Y in the right partition, and the weight of this edge will be the amount we save by sending a team from party X to party Y.
Clearly, if you are sending a team from X1 to Y1 and also sending a team from X2 to Y2, then X1 must be distinct from X2 and Y1 must be distinct from Y2. Hence, any valid way of using N-F teams corresponds to a matching of size F in our bipartite graph. And therefore, the cheapest way to do so is the minimum weight matching with exactly F edges.
(Note that in the above situation it might be the case that Y1=X2. In other words, the same team gets sent to multiple parties.)
And that's it. As we get to use 1 through K teams, we are interested in minimum weight matchings that consist of N-K through N-1 edges.
First, imagine you want to use exactly N teams. The cost is obvious: it's the sum of all distances start-location.
I cannot find why it is impossible to carry equipment using client which was already served. Is it clear from the problem statement?
It is possible to carry equipment from one party to another. Finding the optimal cost of doing so is the actual problem we are solving here. I'm doing that later using the min cost matching, others are doing it using the mincost maxflow.
In the part of my solution you are quoting I'm just computing the cost of one special case: the one where each party is served by a different team. (This special case may not even be a valid solution.)
Let's see, the actual question is:
Why is impossible for two equipments to start by the same party?
It is not clear enough in the problem statement the fact that an equipment can be carried to one party only if this party has not been served by other equipment.
Yes, this was ambiguous. As far as I know, the only global clarification during the contest was the announcement that this is not allowed.
Problem C:
I constructed the graph this way:
Consider the N+1 locations as nodes. Construct an edge from Source to Location 1, with capacity=K, and cost=0. Construct edges from Source to Locations [2..N] with capacity=1, and cost=0. Call the Source as Layer 1, and this set of locations as Layer 2.
Consider a Layer 3, with N+1 nodes. We can consider Layer 2 to be Input Nodes and Layer 3 to be Output Nodes. As per input given in the problem, construct edges from Layer 2 to Layer 3 with cost(i, i + j)
Construct edges from Layer 3 to Sink with capacity=1 and cost=0.
Perform min cost max flow on this graph.
did you got AC with this method? seems pretty wrong to me, especially where you just pump flow 1 to all nodes [2...N]
Yes, I got AC.
For problem L, Do we need to take care of floating point precision issue? May be something like multiplying all the probabilities with 10^2.
Edit: I tried solving the problem and it worked without need of any special care. Can anyone help me how can we prove that there won't be any precision loss in the solution?
Can any one explain complete solution of H and E? I saw the video but its not that clear to me.
Who can explain the answer in the first sample of problem I?
Misof,
regarding problem L/Weather, could you explain how you arrived at 12k equivalence classes?
I assume you mean for n = 20. Do you mean classes of symbol words that have the same number of each weather letter (RSFC)? In this case, I am only able to identify 1771 of them, listed here: http://pastebin.com/ZK0seLyV
You are correct, I was wrong. I also get only 1771 now. I probably accidentally used 40 instead of 20 when doing the calculation seconds before the broadcast :)
Thank you. May I ask a follow-up question. How exactly do you compute the Huffman on the equivalence classes? I've tried a number of attempts without success.
For instance, in testcase 1, the optimal Huffman tree encodes the string "CS" as 000 (3bits) but the string "SC" as 0111 (4bits), even though they have the same probability of occurring. How do you account for that?
There is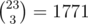 ways to divide sequence of 20 days into 4 groups. Why? Consider 23 empty places in a row. We want to put 3 walls in three different places. It gives us 4 segments separated by walls and their lenghts are our four numbers with sum equal to 20.
ways to divide sequence of 20 days into 4 groups. Why? Consider 23 empty places in a row. We want to put 3 walls in three different places. It gives us 4 segments separated by walls and their lenghts are our four numbers with sum equal to 20.
Thanks — I'm not confused about why there are only 1771 classes — I'm asking how to process those classes when computing the Huffman tree. In the Huffman tree, each class ends up as a combination of multiple subtrees whose numbers of leaves add up to the numbers of elements of that equivalence class. I'm wondering how to find those efficiently. Is there another insight that is needed here?
If you have 15 nodes, each with probability 0.001, you will have 7 nodes, each with probability 0.002, and 1 node with probability 0.001. Then, the single remaining node will get paired with something else.
Here's my AC code if you want to take a look: http://ideone.com/ZhvoD1
Ah, of course. I had made the mistake of dissolving each equivalence class into nodes/subtrees once it reaches the head of the heap/queue, but this is of course not necessary since if you simply insert an equivalence class with probability 2*pp and sz//2 into the queue.
.
Someone know about a site where i can find the solutions in plane text, because i dont have access to youtube, thank in advance?
How to avoid messy code and/or copy-paste in M, where you need to do the moving for 4 directions?
Edit: nevermind
What I did is, for each window I declared two arrays called "pos" (position) and "dim" (dimension) with size 2. Whenever I wanted to use the X positions and the widths I used pos[0] and dim[0], and then for Y positions and heights I used pos[1] and dim[1]. With that, I could simply send this value (0 or 1) as a variable to my procedures, called "dir", and use pos[dir] and dim[dir] throughout my code.
So far the best thing I came up with is this: instead of considering x/y/+/- cases we can transform the whole field by transposing if it's a 'y' query and flipping if it's a negative delta query, and then implementing move only for positive 'x' delta. After Move is done, simply apply the same transform but in the reverse order.
For problem K, the explanation kind of skips over the only difficult part, which is that it's necessary that every equivalence class has equal amount of every color. He just gives one example, and I can't turn it into a proof because of 2 reasons:
First, the difference of cycles is a sum of equivalence classes, but it's not clear that every equivalence class can be written as a difference of cycles.
Second, you want to know something about the sum of the amount of colors, but you only get the difference. The only thing I can come up with is that they are the same mod 2, but that's not enough.
Hmm, I think that the following argument works (but maybe not :).
First, every equivalence class really looks like the example, i.e., a cycle of edges connecting biconnected components. As soon as one believes that this is really an equivalence relation (which requires some proof), this follows because after removing one edge we consider the bridges of the remaining part of the graph, and these lie on a single path in the tree of biconnected components. Adding the additional edge to the path gives us the cycle.
Now we want to argue that the number of edges of color 1 is the same as the number of edges of color 2 for every equivalence class. Consider a single such class, which is a cycle connecting some biconnected components as in the example, and denote these numbers cnt(1) and cnt(2). Consider two big cycles as in the explanation (disjoint except for the edges from the equivalence relation) and "add" them. Then "subtract" all small cycles fully contained in the biconnected components. More precisely: every biconnected component has two nodes where we attach the edges. There is a simple cycle connecting these two nodes because the component is biconnected. This is our "small cycle", and two big cycles are created by taking one of the two possible paths connecting the two nodes from every biconnected component. After adding and subtracting we get that 2(cnt(1)-cnt(2))=0, because the difference on both big cycles and every small cycle is zero. But this really means that cnt(1)-cnt(2) as desired.
Thanks. It's trivial when you think about it, right? ^^
Misof, I am intrigued by your comments about H, Qanat.
I solved it by writing down the cost function in terms of xi and taking its partial derivatives. Setting the partial derivative to zero yields a recursion of xi + 1 in terms of xi and xi - 1, and then I used a binary search to find x1.
Specifically,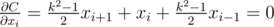
where k = h / w as in your presentation and x0 = 0 and xn + 1 = w for convenience.
You say you would instead use a numerical method — could you elaborate more on how that would be useful? You could solve a system of 10,000 equations with 3 variables each, but that would require that you implement some kind of sparse solver; and in any event, with the equations as given, finding x1 with a binary search seems kind of obvious. Which numerical method that should converge reasonably quickly were you thinking of?
Also, I tried using the method of gradient descent on the cost function with a line backtracking search. This works for small n, but fails to converge in time for large n as I expected.
If I understand you correctly, you are looking for Tridiagonal matrix algorithm..
It is based on Gaussian elimination and, therefore, the word "convergency" is inappropriate. Moreover, it works O(n) instead of Gaussian O(n^3) thanks to the "sparse and arranged" matrix.
Misof was referring to an algorithm that would "converge quickly" but there is no notion of convergence when solving the entire system determistically, or is there?
No, there's not, you're right. I don't know what particular algorithms he meant, but I guess one can use tridiagonal algorithm to solve the matrix equation.
More solution sketches: http://www.csc.kth.se/~austrin/icpc/finals2015solutions.pdf
6-Hour Live Coding with SnapDragon where he goes through the WF problems: https://www.youtube.com/watch?v=fFs8-cTq83k