Hello :)
I was the writer for the Round 2. I'm very sad that the contest platform failed and you couldn't do your best solving them -- for me it's also sad as my work on the problems is now wasted. Hopefully you liked the problems themselves.
Here are the problem statements:
- A http://pastebin.com/raw.php?i=U8SfbSL8
- B http://pastebin.com/raw.php?i=bAi07eMm
- C http://pastebin.com/raw.php?i=R72vqKkk
- D http://pastebin.com/raw.php?i=Ar5CmJ8j
- E http://pastebin.com/raw.php?i=wiCtb0ab
- F http://pastebin.com/raw.php?i=iaMnb9cs
And below are brief solution ideas. Ask if anything is unclear.
A (ascending the stairs)
Dynamic programming in O(n).
Let W[x] be the number of ways to climb the first x steps of the stairs. (We will call that "state x".)
W[n] is the answer we want.
For each x, let y be the lowest state that we can go directly from state y to state x -- i.e., the sum H[y]+...+H[x-1] is still <= m. Then W[x] is simply the sum of W[y] through W[x-1].
Using two pointers, we can find the right y for each x in linear time. We can also maintain the sum of the Ws that corresponds to the current y and x.
B (back to the start)
Compress the coordinates. Then, realize that the optimal curve never has to pass through a corner of the unit square grid (we can always go around it on either side -- if the corner is available, so are the four sides that meet there). Thus we can turn this continuous problem into a discrete one and solve it using BFS. Consider the unit squares around the curve. Build a graph where two unit squares are adjacent iff they share a side and the curve doesn't use that side. Then, start the BFS from all four unit squares adjacent to the start and check whether you can reach at least one of the four squares adjacent to the end.
Generating good test data for this is a lot of fun :)
C (candy game)
This is known as misère NIM. Each color represents a pile in the game of NIM, and the number of candies of that color is the size of the pile.
The optimal strategy is the same as in the classical NIM: the losing positions are precisely those where the xor of pile sizes is zero. But there is one exception: if all pile sizes are 0 or 1, it is reversed: the ones with an odd number of 1s are losing.
Here is a proof: For situations where the largest pile is 1 it is obvious. In all situations where the largest pile has more than 1 token, the player who has the winning strategy in classical NIM can follow the same strategy in this NIM. This player must be the one who will eventually make the move that will lead into a situation with all pile sizes 0 or 1. And at this moment, the player may choose the opposite: if the winning move in classical NIM was to decrease the current pile to 0 she will decrease it to 1 and vice versa.
D (divisibility from last digits)
Obviously, we have to look at the k-th digit (zero-based index from the right) if and only if 10^k is not a multiple of d. Hence, we are looking for the smallest k such that d divides 10^k. This is only possible if d is of the form 2^a * 5^b, and the answer is max(a,b). Note that a can be at most 59. (Some solutions probably failed because they tried too few values for a, instead of simply dividing d by 2 while it still goes.)
E (exactly divisible by sum of largest digits)
The standard first trick is to write the answer as solve(b+1)-solve(a) where solve(x) counts all solutions in [100,x).
To implement solve(x), use three cycles to run through all possibilities for the three largest digits, and then count all numbers with those three largest digits. (I used two cases: I separately count those with fewer than x digits and then for each prefix of x I count those that are smaller than x in the last digit of the prefix. For example, if x is "1234567", one of the subproblems will be to count all numbers of the form "12341..".)
The core of the solution is a memoized recursive function go(a,b,c,found,rem,left) that generates the number from the left to the right. It has the following arguments:
- a,b,c are the three largest digits, with a>=b>=c. E.g., a,b,c = 9,7,7
- found is a bitmask stating which of them I've already used. E.g., found=5 means that a,c already appeared but b didn't.
- the number I have generated so far gives the remainder rem when divided by a+b+c
- left is the number of digits I still have to generate
Note that once I fixed a,b,c I can maintain the remainder modulo a+b+c while generating the number, and I also know that all digits other than a,b,c must be less than or equal to c.
F (fractions)
The simplest O(n log^2 n) algorithm by Patrascu and Patrascu, described in this paper, should be sufficient. (There are faster known algorithms but I didn't want to make the problem too hard.)











The problems were nice (expect for problem C: it appeared on various competitions many times, and e-maxx.ru/algo (a very popular site among Russian competitors) even has the solution for this specific problem: http://e-maxx.ru/algo/sprague_grundy#25).
Thanks for problemset, we still were able to enjoy it (even though submitting solutions was close to impossible, getting statements was fairly easy — ~20-30 refreshes were enough :) ). Personally I would've enjoyed it even more if the announcement that the round is unrated would be published after the end of the contest, but people who prefer sleeping to solving problems would probably disagree with me.
Thanks. Btw, you mistyped the link to the paper (http// instead of http://), please edit.
Fixed, thanks.
Yes, the problems were really nice, probably except for the fact the last one requires specific knowledge and C also benefits people who know the solution right away.
The last one is just Euler-function-related number theory: you need to come up with a way to tell how many of the simple fractions are smaller than some boundary, and the counting you do is the same inclusion-exclusion as elsewhere. The pattern "smaller than n and relatively prime to n" is not just specific to this problem.
I was aware that C is so basic that some people will certainly know it, but I haven't seen it in a contest recently so I considered that acceptable. I mean, if you've seen all the problems everywhere, you are certainly good anyway :) I still think there are way more people who know how to solve the standard NIM but not the misere version and for those this is a nice problem to think about.
BTW, why do you use the pronoun "she" for "player"? I also remember "she"-rabbits and many other examples on programming contests. And I have never seen this in other English texts. I also asked several English teachers about that and all of them said that such usage is nonsense.
I guess the English teachers you asked are pretty old :) Historically people said "he" when the gender was unknown. But some time ago it suddenly became a sign of "sexism", go figure. So now if you don't want any trouble you should always use "she".
I think in modern English the proper pronoun is "they". "She" might be also acceptable, but "he" is widely considered offensive (see e.g. the story behind this pull request on github).
The short answer is "because I can". I usually use the singular "they" if I don't want to talk about gender, but occasionally I go for the female pronouns as well -- to bring some balance to the Force ;)
It's not intended to be any kind of a strong cultural statement, it just feels nice to go against the stream sometimes ;) and it's good that people notice it. If I need to talk about both players, I will usually make one male and the other female. This has both the benefit that the story is "balanced" and the benefit that I can unambiguously refer to each player using a different pronoun.
Still, the problem authors are predominantly males, and even if we aren't doing that consciously, we tend to make male-friendly problem statements. Sometimes it's good to realize that and do something different. The next time you write a story to a programming contest problem, try writing one that would be more interesting to a girl.
(Incidentally, the problems for this round have close to no story at all. That is both because I wanted to keep them as short as possible and because I had close to zero time when writing them :) )
A trivial, D trivial, C well known, B standard, F known and based on paper :(. I have encountered F few times, I already read this paper: http://www.mimuw.edu.pl/~pan/papers/farey-algorithmica.pdf and have it opened during contest, but I was unable to convert it to code at 5:30AM.
I suggest everyone reading this to consider much more challenging version of problem B. We are given n<=1e5 segments (not necessarily parallel to axis) such that number of intersections is not very big (let it be also <= 1e5). We are also given two points (not on segments) and need to state whether they can be connected. We can assume that we are given list of pairs of segments that intersect (there is algorithm which quickly list occurences and is very nice, but that is somehow irrelevant to matter of that question). That problems has very short and beatiful solution!
... says Swistakk who failed the well-known C and the trivial D :P
Sorry for the jab but I think you are way too critical here. Let's see you do a better job at some point in the future ;)
I guess you are entitled to your opinion, but so am I to mine, and mine is that you are being too harsh in your evaluation.
D is indeed trivial for you. That's perfectly fine -- because I'm not writing a problem set just for you. Do you see everyone solving it? You don't.
A is harder than D, and judging by the number of WAs and TLEs, it's not that trivial. Plus, it is significantly different: it is purely algorithmic whereas D needs basic number theory. There are people who solved just either one of those, and there are a lot of people who solved both quickly. Both of those problems worked out exactly the way I intended: the contest wasn't boring for everyone not in the top 100.
C has only 59 correct solutions, most of them submitted after one hour of the contest. Granted, given the "service not available" error this data is not really reliable, but that doesn't really sound that well-known. As I said above, I expected that a few of the top contestants will know it, and that's precisely what happened. Nobody other than Gennady got more than 4 so I guess there was still enough work for those contestants as well.
The "standard" B has only 15 solutions. I agree that this is a problem that is "standard" in its topic. Still, most people will avoid it or fail to solve it precisely because the only solutions they see are the ugly geometric ones that need a lot of heavy duty machinery. This is a problem where the main problem isn't coming up with an efficient algorithm. Instead, the main problem is to come up with a solution that has no special cases and can be implemented in a few lines of code. Is that really so "standard"?
And seriously, what the "F" is wrong with problems based on paper? A contest that can be solved entirely in your head is way too easy. I wrote 6 pages of stuff while solving today's GCJ.
By the way, I have a short solution to your B (as my B was actually a simplification of a similar harder problem) but I don't really find it beautiful. What's the idea you have in mind?
Fully support you on this opinion
When 50-100 best people discussing problems which 2,000 were trying to solve usually sound strange. Everything is "too well-known", "too standard" and "too easy".
Usually when I solved something and particularly happy for my performance — which is not "star" performance, but fulfilling for me — I get to Codeforces to learn that problems I solved were "too simplistic" or simply "Failed problems", like problem B in Yandex Algorithms Round 1A, that the contests where I got some decent place (e.g. getting T-shirt) were badly balanced or badly executed (like this year's Facebook Hacker cup). So my happy state quickly goes away.
I understand that on websites like Codeforeces one you get skewed opinions — mostly of those people who live programming contests, not just participate.
For me problem set was challenging and interesting. I solved just two problems, though still scored within 200, so I am not at 25% bottom of participants. Thank you! It's sad that platform failed.
"... says Swistakk who failed the well-known C and the trivial D :P" — yes, in corresponding subject I already admitted that I have a serious mental disability :D. (I will do not ever send blind submission at 5AM. I will do not ever send blind submission at 5AM. I will do not ever send blind submission at 5AM.)
OK, maybe my feelings are strenghtened by combination of 5 AM and Internal Server Error :P. I admit that it may be the case that I oversimplified my evalution and that problemset consisting of 6 problems meant to be solved in 1:40 should not consist only of problems which are hard for redcoders :P.
And I got a feeling that a funny misunderstanding happened :D. When I said "based on paper" I meant that main idea comes from a scientific publication (which I abbreviated as "paper" :), not that in order to solve this task we need to use pen and paper :D. Though I admit that it is very nice problem!
Idea I have to harder version of B relies on winding number (in fact it's not my idea, but I'm enchanted by it). Simplest solution to come up with is to somehow consider facial cycles and check if there is such face that one point is inside it and second is not. However we do not have to limit ourselves to facial cycles! It is obvious that if we find any cycle that has different winding numbers wrt to our points then they can't be connected. We build a graph where intersections are vertices and pieces of segments between consecutive intersections within one segment are edges (though we do not even need "consecutive" here!). We run DFS on that graph and check if it encountered any cycle such that those winding numbers are different. If it finds one then answer is obviously "no", but what if it doesn't? The trick is that in this case answer is yes! Proof of this is highly nontrivial and beatiful.
Consider any cycle in that graph. It is a linear combination of all facial cycles contained in its interior (formally, we consider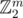 space). It follows that facial cycles generate subspace of that space such that each vertex has even degree and it has dimension equal to number of bounded faces, which by Euler's formula is equal to m - n + 1. It can be easily seen that cycle DFS found are linearly independent since each such cycle has one own nontree edge. There are m - n + 1 such edges, so subspace generated by them is exactly the same subspace as previous one (their dimensions are equal)! Since that, facial cycles are also contained in it, so it is sufficient to check just DFS cycles!
space). It follows that facial cycles generate subspace of that space such that each vertex has even degree and it has dimension equal to number of bounded faces, which by Euler's formula is equal to m - n + 1. It can be easily seen that cycle DFS found are linearly independent since each such cycle has one own nontree edge. There are m - n + 1 such edges, so subspace generated by them is exactly the same subspace as previous one (their dimensions are equal)! Since that, facial cycles are also contained in it, so it is sufficient to check just DFS cycles!
What we need to code is almost no geometry (we do not even need that consecutiveness of intersections on edges), so only geometrical thing we need is counting winding number which is done with every step of DFS and that is whole solution :))).
Oh, now I get what you were saying about F! :) It's indeed a funny "paper" vs. "paper" misunderstanding.
The problem is actually not based on the paper, it's more the other way round. I know it from Mihai, and he wrote the paper after thinking about the problem and I believe that back then at least a part of his original motivation was also to set it as a problem in some contest. Now I just linked to the paper because I was lazy to type the solution into the editorial :)
Can you give an example to combine the problem with winding numbers?
If point is inside a cycle then it's winding number wrt to that cycle is either 1 or -1, if it's not then it's 0. Winding number is pretty much the same as ray casting algorithm of checking whether point lies inside polygon. I think there's not much anything more to it here.
Isn't the way to build graph which uses the intersection of two polyline as vertices and two adjacent vertices as edges? Then count every cycle and winding numbers?
Hi Michal, thanks for the nice problem set (and sorry about the internet issue)
Could you post your code for task E? I have implemented something similar, but it was 10 times slow..
Sure. Here it is: http://ideone.com/9pHuFs
For all rounds, the problems will be original.So you violated this rule consciously (I don't criticize you, but violations of this rule already happened in at least three rounds, so it looks like this rule is ignored by problem coordinators)?
I was not told any rules :)
Anyway, "originality" is very ambiguous. I believe that if the organizers made the above promise, you should interpret it as "we will not copy problems from older contests" (which is something that can be guaranteed) and not as "we will guarantee that nobody ever saw anything similar to our problems" (which is something that you cannot reasonably guarantee).
when 2nd round will be held?
I still can't understand your solution of problem B. Can you explain it using an example?
misof, can we submit solutions to these problems somewhere? If not, can you share the test data?