How can we prove this : no of unique outputs to (i*j)%k where i can be any number j and k are known is k/__gcd(k,j);
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | djm03178 | 152 |
| 7 | adamant | 152 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/23/2025 10:25:32 (k1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










You need to find for which a there exists a solution to ij ≡ a (mod k) where i is a variable. Obviously if (k, j) = 1 then j has an inverse mod j so for any a < k there exists an unique solution.
Now suppose (k, j) = d! = 1, then your equation becomes equivalent to finding an l such that ij = lk + a or ij + ( - l)k = a. A pair i, l exists if and only if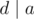 , so a = dx where x has some random value. Now you have d * x < k so x < k / d, so x can range from 0 to k / d - 1, so there are exactly k / d variables for which there exists a solution.
, so a = dx where x has some random value. Now you have d * x < k so x < k / d, so x can range from 0 to k / d - 1, so there are exactly k / d variables for which there exists a solution.