Hi,
Just wanted to double check if my solutions for Distributed Code Jam practice problems are reasonably correct. This is not the full description, but just ideas on how to solve:
Sandwich
Cut sandwich into number_of_nodes pieces. Every node is responsible for delivering four numbers to central node. Four numbers being "maximum eating from the left", "maximum eating from the right", "total sum", "maximum eating from both ends". Central node having all this numbers can do any algorithm (even O(n^4) if you wish) to come up with an answer, as n is not more than 100 at that point.
Majority
Population is split evenly between every node. Every node sends to central node the best candidate and the runner-up candidate. Central node combines No'1 and No'2 candidates and picks two most frequent (maybe one is enough?). Central node sends request to all other nodes to provide vote count for two most frequent candidates. Nodes respond, central node adds votes up and produces result. (UPD — wrong approach — see in comments below)
Shhhh
I found it most interesting. My solution went like this — we have to go through the whole circle to get the answer, there is no way around it. We want to split work across nodes, but we can't do it evenly, as we don't know where each person sits. Randomization helps (was it intended solution?). I played with numbers a little bit to see that if we have 100*number_of_nodes "key numbers", every node can start from each of it's 100 key_numbers and go right until getting to another key_number. Then send to the central node information in form "from key number x to key number y distance is D". Central node combines all this data and give out result. I think we are protected by statistics from situation where one node might get unusually long sequence leading to TLE.
Load Balance
Classical partitioning problem. I only used 8 nodes for small and 64 nodes for large (not 100). With 52 numbers you can split them into 64 sub-tasks with 45 numbers each. 45 numbers are solvable by "meet in the middle" algorithm for sub sequence sum search. So each node receives 45 numbers and sum to search for. Sum to search for is Total / 2 adjusted depending on whether you include first 7 numbers in this sub-task or not.











I think the ideas you have work (and I guess that your result proves them :) ).
I think that for Majority, it is possible to craft a test case that defeats your algorithm, but it's really hard to actually make sure that it will be defeated (since I don't know what exact heuristic you use, and what split between nodes will you make). In a sense, it's a randomized algorithm :)
The testcase is basically as follows: On 1/4 of the nodes, you get all votes for A, and one vote for B. On 1/4 of the nodes, you get all votes for A, and one vote for C. On 1/4 of the nodes, you get 1/3 votes for B, 1/3 for C, and 1/3 — 1 for A. On 1/4 of the nodes, you get 1/3 votes for B, 1/3 for C, and 1/3 — 1 for A.
A is the clear majority (with roughly 2/3 votes). However, B and C are reported as one of the top two by 3/4 nodes, and A is reported only by 1/2 nodes, so your algorithm would treat B and C as global candidates.
I see, however, multiple ways of modifying this heuristic in also incorrect ways that will defeat this testcase; this basically made this a problem not suitable for a real round :(
For Load Balance, your solution works, but it's O(2^(N/2) / sqrt(M)). There is a randomized solution that runs in O(N 2^(N/2) / M) — which is actually worse for this problem, but is "perfectly parallelized" — that is, it scales better with the number of nodes.
Thank you for first-hand response. Based on your comment I'll definitely focus on other contestant's solutions for majority and try to find something on that perfectly parallelizable idea for Load Balance — any more clues on where to look? ;)
It seems that algorithm I used can be parallelized, but only into powers of two (64 nodes or 128 nodes, not in between).
I think the correct idea for majority is based on the fact that if there is a global winner then it should win in at least one node no matter how you split the nodes. So you calculate all local winners and then pass them back to all nodes to get their full score and choose the global winner.
Thank you!
It makes perfect sense — as candidates has at least 50% + 1 votes, there must be at least one group where he won.
It wouldn't work if we were just searching for the top candidate, but as we are searching for majority candidate — this is it.
Honestly when I was solving it, biggest challenge for me was to get that simple idea that central node can process something, then ask other nodes AGAIN for additional information — I just didn't think about it at first. Then I was trying to limit size of second query, which was not a good idea as I see now. Should have gone with full 100 candidates.
For both shhhh and sandwich I get bigger runtimes on small cases than large ones. Is there any possible explanation?
Actually for shhh going from single vertex on each node is enough
Probably for given constraints it is enough, but it result in worse complexity. If I recall correctly if you pick n random points on unit circle then biggest space between two consecutive points should be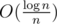 , so we get another
, so we get another 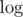 factor. If we will start from many points then this log disappears.
factor. If we will start from many points then this log disappears.
I cannot see why it will disappear. Though with more points it should be faster, yes, I just not sure asymptotically faster
Hmmm... Intuitive argument goes like this. If we will consider 100 points assigned to one node then it is 'impossible' for all/many of them to fall in large gaps. I guess that rigoristic argument should use either some estimation of variances or if it won't work then central limit theorem.
Actually thinking about it this should not help at all — why total length of k out of nk segments should change between randomly selected segments or consecutively selected ones?
Uh, you got me for a moment and I really doubted my intuition, but I believe it again :D. In fact random nd consecutive k segments are the same thing, but I think that fault with your argument is that k consecutive segments out of nk of them is something very different from 1 out of n of them. If you will take n random points then large gap will appear, but if you will add (k-1)n new points then many of them will fall into that large gap, much more than k-1!
Probably it means that if you continue increasing number of dots in proportion to log(n), log factor disappears. And 100 dots already covers A LOT LARGER n.
I came up with idea of making more points only because I was afraid of overrunning the time limit. I couldn't make Parunner work with release version of my code (still can't — somehow number of nodes becomes zero when I switch to release version and I get division by zero), and debug version gave me very uncertain feeling about performance.
See my comment above. Expected maximal total number of moves by one node should not really change until total number of special nodes are comparable to total number of nodes
My intuition is like this:
The main issue we have with this algorithm is Standard Deviation of lengths each node has to run through.
Comparing two situations:
In second case Standard Deviation of total length will be much smaller — I think you should divide Standard Deviation by sqrt(N), which is 10 here.
So the busiest expected node should be much closer to the mean. Not sure by how much. Maybe log factor.
Yeah, that argument with standard deviation is very clear here. In fact that is approximately the same what I meant by estimation of variances :). However there is slight overlooking here, because those random variables corresponding to random distances are not independent :(... But they are "almost independent", it is clear that their dependence is very small and I'm sure that it can be somehow proven that it doesn't matter much, but I have other things to do now :P.
Btw, of course 100 was not used as 100 in a general case xD. Of course if we will start from constant number of points on one processing unit then it won't change anything asymptotically, but if we will replace 100 by some sufficiently fast growing function then we will get even distribution of work.