I am learning DP and I am a litle frustrated. I am stucked in this problem http://codeforces.net/problemset/problem/466/C I drew some pictures to find out some states this is the image http://i61.tinypic.com/de4rpe.jpg theres is a pattern in these pictures to get this formula n = n — 2 numberOfTotalCombinations = n * (n-1) / 2 the worst case(5 * 10^5) would be = 124999750000 and it will not pass. My questions Should I consider all the combinations? How to define my states? How I need to construct a DP solution based on the previous states? Thansk in advance and sorry for my bad english
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
28:14:55
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
28:14:55
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 13:20:05 (h1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|










No, you shouldn't consider all combinations. This is DP, it's all about avoiding cases where you can't get a result. This problem is solved this way: Let: x=sum(k=1, i-1)a[k]; y=sum(k=i, j)a[k]; z=sum(k=j+1, n)a[k]; and s=sum(k=1, n)a[k], the sum of all numbers in the array We observe that x+y+z=s, and how x=y=z (that's what the problem states) => 3*x=3*y=3*c=z, thus x=y=z=s/3. You can figure it out from here, but here is the rest of the solution (dont't read unless you gave up on the problem): Let v be an array such as v[i]=sum(k=1, i)a[k]. If vn is not divisible by 3, that means we can't divide s into three equal parts. Now, we will work with the sums in the array v. So, how x=y=z=s/3, we need to find all sums equal with s/3. The number of ways we can achieve that sum is the number of x's we can obtain. Afterwards, when we can no longer obtain s/3, we try to obtain 2*s/3 (from array v), that is x+y. When we find one, we add the number of ways of getting x to the solution. The code looks something like this: http://codeforces.net/contest/466/submission/11713930
If you consider all possible combinations, then it's not DP, but brute froce. Anyway, this problem is something else.
Let S be the sum of all elements. First of all, if that sum is not a multiple of 3, then the answer is 0. OK, now calculate Li, which means how many positions p are there with p ≤ i such that the sum of all elements from 1 to p is equal to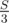 . Then iterate from the right (from N down to 1) and keep track of the sum of all elements so far. If at position i, that sum is
. Then iterate from the right (from N down to 1) and keep track of the sum of all elements so far. If at position i, that sum is 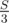 , add Li - 2 to the answer (you must have at least one element in the middle section).
, add Li - 2 to the answer (you must have at least one element in the middle section).