rossatron's blog

Summation of a weird function.
By rossatron, history, 9 years ago, In English

I found this question at http://math.stackexchange.com/.

Let n is a positive integer.

n = p1e1p2e2... pkek is the complete prime factorization of n.

Let me define a function f(n)

f(n) = p1c1p2c2... pkck where ck = ek - 1

Example:

72 = 2332, so f(72) = 23 - 132 - 1 = 2231 = 12

144 = 2432, so f(144) = 24 - 132 - 1 = 2331 = 24

Now let

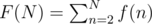
Example: F(10) = 1 + 1 + 2 + 1 + 1 + 1 + 4 + 3 + 1 = 15

Now I want to evaluate F(N) for a fairly large value of N, say 1012. Can I do it without factorizing each number?

It appears quite interesting. I think maybe it requires some kind of inclusion-exclusion, but so far was unable to implement. Any idea how to solve?

  • Vote: I like it
  • +31
  • Vote: I do not like it

Comments Comments (10)
| Write comment?
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

If the constraints on this problem are smaller like say N <= 10^6 then it can be solved using sieve only.

→ Reply
»
9 years ago, # |
  Vote: I like it +47 Vote: I do not like it

Notice that there is small number of different values for f(n).

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Yeah, I noticed that. For the squarefree numbers f(n) is always 1. Many numbers are mapped to same f(n). But how can we use this to calculate F(N)?

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +21 Vote: I do not like it

      It seems that it should be possible to calculate for how many numbers f(n) = x holds, given x.

      If x = p1^c1 * p2^c2 * .. * pk^ck then n = p1^(c1+1) * p2^(c2+1) * .. * pk^(ck+1) * r1 * r2 * .. * rt where r1..rt are distinct primes different than p1..pk.

      So you basically want to know how many square free integers (with no prime factors in p1..pk) are there between 1 and N/(p1^(c1+1) * .. * pk^(ck+1)).

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
        ← Rev. 3   Vote: I like it 0 Vote: I do not like it

        Wow, that is a superb idea. I shall try to implement it. Thanks.

        There are 7 square-free numbers <= 10 : 1, 2, 3, 5, 6, 7, 10.

        f(n) = x

        x can take the values 1, 2, 3, 4

        C(x) = No. of integers for which f(n) = x

        C(1) = No. of square-free numbers less than (10/1) = 7

        C(2) = No. of square-free numbers less than (10/4) = 2

        C(3) = No. of square-free numbers less than (10/9) = 1

        C(4) = No. of square-free numbers less than (10/8) = 1

        Here the sum F(N) is defined for n = 2 to N, so C(1) = 7 — 1 = 6

        But we are counting 8 twice, for c(2) and C(4). How can I remove the duplicates?

        → Reply
        • »
          »
          »
          »
          »
          9 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Yes, those square free numbers should be coprime with x. So you should count 8 only in C(4) because f(8) = 4. You should be able to modify your square-free counting algorithm to not count numbers that have common prime factors with x.

          → Reply
        • »
          »
          »
          »
          »
          9 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          Counting squarefree numbers is a classical problem. The conclusion is really interesting.Check it out HERE.

          Use Möbius function, U can do it in .

          → Reply
»
9 years ago, # |
  Vote: I like it +27 Vote: I do not like it

Let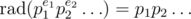 . We know that 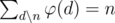, so

If d divides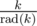 , then 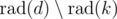and 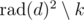. Let's replace k with :

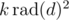Now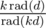 can be replaced with k, as it doesn't change any prime factors included in 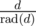. So again let's replace k with :

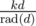As there is a bijection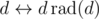 , let's sum over values of :

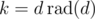The sum is over numbers with all prime factors powers greater than 1 (squarefull numbers), I guess there should be about of them, so it should be fast enough for n = 1012.

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Thanks for the wonderful explanation. What does the last term [rad(k)2 k] means? Is it k is divisible by rad(k)2, or just ?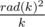

    There are 2158391 square full numbers  <  = 1012, so the sum can be indeed calculated in reasonable time.

    → Reply