helpme's blog

Help needed in counting problem
By helpme, history, 9 years ago, In English

Hello everyone,

I need some help understanding the solution of a problem. The problem is, find the number of ways to represent a number. For example, 4 can be represented in 8 ways: 4, 1+3, 3+1, 2+1+1, 1+2+1, 1+1+2, 2+2, 1+1+1+1

After some calculation I found that, answer of this problem is f(n) = 2^(n-1). e.g.

f(1)=1
f(2)=2
f(3)=4
f(4)=8
f(5)=16

can anyone explain why the answer is 2^(n-1) ? Thanks in advance!

  • Vote: I like it
  • +1
  • Vote: I do not like it

»
9 years ago, # |
  Vote: I like it +4 Vote: I do not like it

Imagine you have n apples and want to split them into the boxes, so in each box you have at least 1 apple. You put apples into the row and add separators between some. There are n - 1 possible places for separators and each subset of set of possible separators is correct( there are 2^(n — 1) subsets). Now you need just understand that it is the problem you've written above :)

→ Reply
»
9 years ago, # |
← Rev. 3   Vote: I like it +3 Vote: I do not like it

you know that every number(for example n) can written by n number 1 so every way can be written by some 1 in this way.

5=2+3 --> 5=(1+1)+(1+1+1)

also we know that if you have n number 1, you can make all of the answer for example:

1+1+1+1+1=5 --> (1+1+1)+(1+1)=3+2=5

or

1+1+1+1+1=5 --> (1+1)+(1+1)+(1)=2+2+1=5

so we suppose that we have n number 1 and know I want to make all the answer thus it is need to discuss on the number of parenthesize of the answer.if want to divide it to k parenthesis we have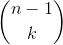 way to do it and since that k is a variable between 1 to n the answer is:

Excuse me if I explain bad.

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Imagine you have N ones written in a row. Now to represent N like a sum, you have to separate your summands.

There're exactly N - 1 places (between consecutive ones) where you can separate or do not separate. So the answer is 2N - 1

→ Reply