| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
What is the sum of number of divisors of divisors of number which is smaller than n, such that sum of number of divisors of divisors of this number is maximum?
For example,
g(n) = number of divisors of n
f(12) = g(1) + g(2) + g(3) + g(4) + g(6) + g(12)
f(12) = (1) + (2) + (2) + (3) + (4) + (6) = 18
Can you help about it?
What is the problem source?
There is no source. I found it in one of my old codes.
http://codeforces.net/contest/439/submission/6821984
The complexity of f function is equal to this.
What's the source of your problem?
Edit: perfect timing :)
If given x then f(x) would be product of (αi + 1)(αi + 2) where αi is degree of ith prime which divides x. It is possible to make DP for small values of x, but I don't see how to solve problem for large x > 107. Ups typo.product of (αi + 1)(αi + 2) / 2. Anyway, how to solve easier problem: find maximum g(x) where x < n for 0 < n < 109.
Auto comment: topic has been updated by kalimm (previous revision, new revision, compare).
Almost a palindromic topic :P
Let's factorize your number x. For example, x = x1α1 * x2α2 * ... * xnαn
Let's take one of it's divisors. For example, it's y = x1λ1 * x2λ2 * ... * xnλn where λi < = αi.
It's obvious that divisors of number y is (λ1 + 1) * (λ2 + 1) * ... * (λn + 1). Than total sum is
. To found it's sum, you can run all possible λ, e.g. all divisors of x, it's not too much, something like log(x). I don't sure that you really need to count sum really fast, because factorization seems longer than sum.
Edit: you can count this sum quickly, it's easy.
Let
It means that
Than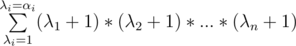
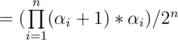
ACM-ICPC Asia Regional contest dhaka site ........... Problem-(E) needs this concept. Problem link : http://www.northsouth.edu/acm-icpc-2015/Problem_Set_2015.pdf
Nope. That is simply the sum of divisors. Not sum of sum of divisors :P