HI Folks,we Have SRM tomorrow at Time
Good luck to everyone.
Let us discuss problems here after the end of the contest
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 3898 |
| 2 | tourist | 3840 |
| 3 | orzdevinwang | 3706 |
| 4 | ksun48 | 3691 |
| 5 | jqdai0815 | 3682 |
| 6 | ecnerwala | 3525 |
| 7 | gamegame | 3477 |
| 8 | Benq | 3468 |
| 9 | Ormlis | 3381 |
| 10 | maroonrk | 3379 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 165 |
| 3 | Dominater069 | 161 |
| 4 | Um_nik | 160 |
| 5 | atcoder_official | 159 |
| 6 | djm03178 | 157 |
| 7 | adamant | 153 |
| 8 | luogu_official | 151 |
| 9 | awoo | 149 |
| 10 | TheScrasse | 146 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jan/31/2025 16:50:51 (k2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Why the downvotes?
Where is chrome?
I was the author for this round. Here are some hints and code:
code here:
all of div2: http://pastebin.com/YtdPjtHm
all of div1: http://pastebin.com/xSEVNXmW
Some vague hints
div2 easy: Suppose you just wanted to reduce time by 1 second. What's the best strategy in this case?
div2 med: The first step is to clearly define the state of the game. Then, you need to determine how to classify states as either winning or losing.
div2 hard: For each node in the tree, you can find some intervals of time where you definitely need to do one switch in that interval. How can you generate these intervals? Afterwards, does this modified problem look familiar?
div1 easy: Given an output rate, can you determine if the tank will overflow?
div1 med: The first step will be to compute some sprague grundy numbers. Can you see any patterns?
div1 hard: 2 different approaches
1) Given a time, can you compute the minimum budget needed to achieve this time?
2) Suppose you just wanted to reduce the time by 1. What's the best strategy in this case? (I'm not sure how to prove it, but it seems to pass all tests).
>(I'm not sure how to prove it, but it seems to pass all tests).
Isn't that risky? Especially in competitions with challenges.
I implemented the first approach as reference, which I know how to prove. I thought the second was interesting to mention, but I'm not sure why it works.
Oh, I misread that part.
It seems I could've solved 450 much more easily — I tried to find a pattern on paper, but it failed, so I just wrote a bruteforce for Grundy numbers, tried finding a period of Grundy numbers for some random tests (because they should be periodic if it's just 450 :D) and found out that it's 2 for large enough k...
Well, if the first approach can be proven then it's ok.
The second solution uses critical path, looks like a well researched method so it's probably proven somewhere already.
Strange solution for div1 hard that passes all systests: http://ideone.com/knlGNZ
Basically, generate all paths from vertex with indegree 0 to a vertex with outdegree 0, then solve a linear program inside a binary search to find the answer.
Seems to pass all system tests in at most 14ms (!), but I didn't have much confidence in this during the contest so I missed submitting by a few minutes :p.
I think this solution is correct, because maximum number of edge is 50.
For div2 Med : It is possible to determine the winner of the game in O(1).Some case analysis needed . My solution : Link
In div1 med of referenced implementation I found this code:
How this can be proven/inferred without generating any sprague grundy values? Is mentioned hint about it?
Failed System Test Div1/250 :'(
How can you determine a good number of iterations for a floating-point binary search? I always make the same mistake of using an epsilon as a stop condition :(
It was a very silly mistake :'(
A better approach in such situations is to manually set the no. of iterations ( >= 300 is fine)
Suppose [L; R] is the search range and P is the number of digits after floating point you should calculate.
log2(R - L + 1) + log2(10P) + C will be enough for C <= 5.
In today's 250p you could just set the number of iterations to 1024 and fit into the TL comfortably.
I also used epsilon and passed. You just have to make sure that it's not too small; since the required precision is 10 - 6, I set it at 10 - 7. And the initial max. R at 106.
I don't trust in the epsilon as the stop condition anymore :(
It cost my team a problem in the ACM ICPC Latin America Regional contest of this year (a ternary search with dijkstra), and now this xD
Thanks guys!
What is at least one reason not to use epsilon as stop condition, what caused a problem here? I was used to perform constant number of iterations, however recently I got 2 TLEs in 2 different problems within few days, because I set that constant a bit too high and after changing this to epsilon condition it passed, so now I think that eps condition is a safer way. However we should be aware that epsilon condition is applicable if value we are searching for is exactly what we want to output, I mean such thing will be bad:
"Print result with error not larger than 10 - 6."
because maybe it doesn't hold that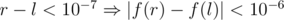
When L and R are something large while eps is very small, it can go into the dead loop — (l+r)/2 will be exact l or r.
I failed by this reason 6 years ago: https://community.topcoder.com/stat?c=problem_solution&rm=303097&rd=13909&pm=10563&cr=22769059
I heard this kind of problem can be dealt with in the following way: Let's not subtract r from l :-) . We may define h=r-l and halve it after each step. The while condition will be h>eps.
But I only heard about it and never used it. Iterative search seems more reliable...
I was able to cruze for first two problems div2 with comfort, but had no idea how to solve div2 hard, can anybody explain how to solve ? I did not get lewin solution
I haven't coded it yet, so not 100% sure if it will work, but this is the best I could come up with.
We can easily figure out the path (sequence of nodes) required for each train.
Then we can figure out at what time, which nodes need to be in what state, eg(node 2, R).
If we figure out all possible changes required to all possible nodes, and sort it by time, and then make the change at the top of the sorted list, followed by all possible changes, such that the same node is not changed twice (i.e stop changing node k, if it's ith iteration is different from it's first iteration in the list, and don't change it in this action) , in the same action, deleting the changed items from the list.
Repeat till empty list, the number of times we had to iterate is the answer.
I couldn't code this during the contest (ran out of time). Will try coding this after classes today.
Look at some specific node. For each train that passes through this node you will get an information "at time t[i]+epsilon the switch needs to point in the direction dir[i]".
For example, you can obtain the information (3,left), (5,left), (12,right), (15,right), (33,left).
Then, this particular node needs to be flipped twice: once in the interval (5,12] from left to right and once in (15,33] from right back to left. This is possible if and only if there is an action during each of these intervals.
So, now you have a collection of intervals and you want to cover all of them using as few actions as possible. To do this, just notice that it never hurts to perform the actions as late as possible. For example, if your intervals are ( l[i], r[i] ], it makes no sense to perform the first action sooner than at min(r[i]). This allows us to solve it greedily: always find min(r[i]) among intervals that don't contain any actions yet.
Finally uploaded my screencast