I was searching for this well-known technique, but I couldn't find any good tutorials about it, so I had to figure it out myself. And now I want to write my first contribution. The binary lifting method for answering LCA queries is explained in many places, like this, this and this (the method with cost ). I'll explain it one more time, emphasizing how it can be adapted to answer queries about paths on weighted trees (static version, so topology/weight updates are not supported).

Suppose we have a weighted tree G = (V, E), where V = {1, 2, ..., n} and 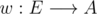is the weight function. First, we need to define some things, which can all be calculated with a simple DFS:

1. p(u) is the parent of vertex u in the DFS spanning tree. p(r) = r, if r is the root.

2. pw(u) is the weight of the edge from u to its parent, p(u). Therefore, pw(u) = w({u, p(u)}). If r is the root, pw(r) must be the identity element of your query, like ∞ for min, or  - ∞ for max.

3. L(u) is the level of vertex u and is defined as L(u) = L(p(u)) + 1. L(r) = 0, if r is the root.

This method is interesting because it combines dynamic programming and divide and conquer paradigms. Let f(u, i) be the 2ⁱ-th ancestor of vertex u. So what is the recurrence relation? How can we break path from u to its 2ⁱ-th ancestor into pieces, so we can compute it more easily? Stop and think. If we're storing ancestors in powers of two, how about breaking the path in its half? Which vertex is exactly in the middle of u and its 2ⁱ-th ancestor? Yes, its 2^i - 1-th ancestor. More precisely, f(u, i - 1). So the acyclic recurrence is

and the base case is

The greatest i that makes sense for f(u, i) is such that 2ⁱ = O(n). So 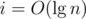. Then we have 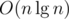DP states and computing one state costs O(1). Therefore, preprocessing will take up to 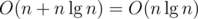operations (DFS + DP).

The intuitive algorithm to find LCA(u, v) using f(u, i) follows:

1. Let r be the root. Choose u to be the farther vertex from r of u and v. In other words, swap u and v if L(v) > L(u).

2. Let 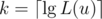. Set u to be its ancestor in the same level of v, climbing up the tree. This can be done with 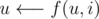, for i = k, k - 1, k - 2, ..., 0, if, at each iteration, f(u, i) is still not above v, that is, if L(f(u, i)) ≥ L(v).

3. At this point, if u = v then LCA(u, v) = v and we can stop the algorithm.

4. Finally, climb up the tree with u and v. In other words, make 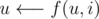and 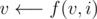, for i = k, k - 1, k - 2, ..., 0, if, at each iteration, f(u, i) and f(v, i) are still not above their LCA, that is, if f(u, i) ≠ f(v, i). At the end of this stage, p(u) = p(v) is the LCA we seek.

No doubt, this algorithm runs in 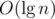time. Now, let's observe the strategy it is based on. First, we climb the path from u to its ancestor in the same level as v, then we climb from v and this new u to their LCA. Note that all these jumps split the path between original u and v vertices in disjoint paths. Therefore, we're actually dividing the problem in smaller disjoint subproblems. This is the principle of divide and conquer and all those algorithms and data structures for RMQ and LCA. So is easy to adapt the algorithm described above to answer queries about paths in the underlying tree. All we need is to define a function g(u, i) to give the optimal (or total) result for path from u to its 2ⁱ-th ancestor, which can be formally defined as

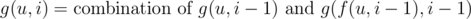
and

The adaptation to the 4-stage algorithm described above is very simple. Start the answer with the identity element of your query (like ∞ for min, or  - ∞ for max). Whenever you make 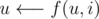or 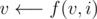(stages 2 and 4), improve the answer with the respective result: g(u, i) or g(v, i). If stage 4 is actually executed, then is necessary to improve the answer with pw(u) and pw(v) in the end. That's all!

Thanks to dalex for the insight (here).

For more dynamic versions of this problem, we have:

1. Heavy-light decomposition (here and here), so you can update weights.

2. Link cut trees (here), so you can update both weights and topology.

Both HLD and LC trees can answer queries in 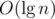time, but they're harder to code and understand.