Так как остальные задачи я не то что не пытался решить, а даже не читал, публикую те решения, которые узнал
Задача A. Домино
Для начала поймём, что на квадраты 2x2 всё поле разбивается однозначно и это можно сделать жадным алгоритмом. Теперь у нас есть 14 квадратов. Далее можно сделать необязательное преобразование, от которого лично мне стало жить проще: построим граф на 14 вершинах, ребро между вершинами будет тогда и только тогда, когда у соответствующих квадратов есть общая доминошка. В принципе, это даже какой-то оптимайз по времени, но не суть важно.
Теперь задача такова: есть граф на 14 вершинах, надо раскрасить их в цвета от 0 до 6 так, чтобы все рёбра были разными (два ребра одинаковы, если цвета концов совпадают). Утверждается, что решение - перебор. Перебираем цвет первой, второй, третьей, ..., 14й вершины, на каждом шаге проверяем, что у нас не появилось ребро той же расцветки, что уже было (естесственно, делаем это массивом bool'ов). После чего останется вывести ответ и какую-нибудь раскраску.
Однако это решение может не зайти по времени. Остался один мощный оптимайз. Заметим, что, по сути, разницы между цветами нет. Значит, цвета в раскраске можно переставлять как угодно. Теперь научимся считать количество ответов с точностью до перестановок цветов, а в конце домножим его на 7!=5040. Это просто: достаточно ввести условие, что цвет очередной вершины либо встречался раньше, либо идет сразу после максимального использованного цвета. Например, после цветов 0 1 2 1 0 2 могут идти только цвета 0..3.
Чтобы уверовать в то, что это решение зайдёт, можно грубо оценить количество ответов. Каждая вершина раскрашена в один из семи цветов, каждый цвет встречается ровно два раза, плюс мы не учитываем различные перестановки. Итого получается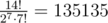 , что, очевидно даже при отсечении на последнем шаге рекурсии, влезает в TL.
, что, очевидно даже при отсечении на последнем шаге рекурсии, влезает в TL.
Теперь задача такова: есть граф на 14 вершинах, надо раскрасить их в цвета от 0 до 6 так, чтобы все рёбра были разными (два ребра одинаковы, если цвета концов совпадают). Утверждается, что решение - перебор. Перебираем цвет первой, второй, третьей, ..., 14й вершины, на каждом шаге проверяем, что у нас не появилось ребро той же расцветки, что уже было (естесственно, делаем это массивом bool'ов). После чего останется вывести ответ и какую-нибудь раскраску.
Однако это решение может не зайти по времени. Остался один мощный оптимайз. Заметим, что, по сути, разницы между цветами нет. Значит, цвета в раскраске можно переставлять как угодно. Теперь научимся считать количество ответов с точностью до перестановок цветов, а в конце домножим его на 7!=5040. Это просто: достаточно ввести условие, что цвет очередной вершины либо встречался раньше, либо идет сразу после максимального использованного цвета. Например, после цветов 0 1 2 1 0 2 могут идти только цвета 0..3.
Чтобы уверовать в то, что это решение зайдёт, можно грубо оценить количество ответов. Каждая вершина раскрашена в один из семи цветов, каждый цвет встречается ровно два раза, плюс мы не учитываем различные перестановки. Итого получается
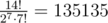 , что, очевидно даже при отсечении на последнем шаге рекурсии, влезает в TL.
, что, очевидно даже при отсечении на последнем шаге рекурсии, влезает в TL.Задача B. Надмножество
Задача была немножко (или множко?) идейной. Одним из возможных решений является разделить множество точек пополам веритикальной прямой (если не получается ровно, та так, чтобы разница была минимальна), решить задачу рекурсивно для двух половин, и добавить на разделяющую прямую точки со всеми встречающимися в ответах для половин y'ами.
Докажем корректность. Если точки лежат в одной половине, всё мы верим, что верно решили подзадачу. Если же они лежат в разных половинах, то их bounding box пересекает нашу прямую, и в точках пересечения выделенные точки есть (посльку их y'и встречались слева и справа).
Прошу сообщество рассказать остальные задачи в комментариях
Докажем корректность. Если точки лежат в одной половине, всё мы верим, что верно решили подзадачу. Если же они лежат в разных половинах, то их bounding box пересекает нашу прямую, и в точках пересечения выделенные точки есть (посльку их y'и встречались слева и справа).
Прошу сообщество рассказать остальные задачи в комментариях










