620A - Робот профессора GukiZ
Легко видеть, что ответ в задаче равен max(|x1 - x2|, |y1 - y2|).
Сложность: O(1).
620B - Калькулятор дедушки Довлета
В этой задаче достаточно было пройти по всем числам от a до b и прибавить к ответу количество сегментов, необходимое для отображения очередного числа. Для подсчёта этой величины нужно пройти по всем десятичным цифрам числа и прибавить к ответу количество сегментов, необходимой для отображения очередной цифры. Последние величины можно просто посчитать по картинке и вбить в один массив.
Сложность: O((b - a)logb).
620C - Жемчужинки
Будем решать задачу жадно. Давайте набирать жемчужинки в самый левый хороший подотрезок по одному, начиная с первой жемчужинки. Как только подотрезок станет хорошим (то есть встретится повторение) начнём набирать новый хороший подотрезок. Если мы не смогли набрать ни одного хорошего подотрезка, то ответ - 1. В противном случае, в конце массива может остаться некоторое количество различных элементов, их нужно отнести к последнему набранному отрезку. Легко доказать, что такая жадность правильная: нужно рассмотреть первые два отрезка в оптимальном ответе и понять, что второй отрезок можно расширить пока первый не станет размера первого подотрезка в нашем ответе.
Сложность: O(nlogn).
620D - Профессор GukiZ и два массива
Случаи когда нужно сделать одну операцию или их не нужно делать вовсе легко разобрать в лоб (за O(nm)). Теперь рассмотрим случай когда нужно сделать две операции. Заметим, что можно считать, что после двух операций два элемента первого массива перейдёт во второй массив и наоборот, поскольку в противном случае то же самое можно сделать и за одну операцию и значит мы уже рассмотрели этот случай. Давайте переберём пару чисел, которая перейдёт во второй массив и сложим суммы в некоторую структуру данных (например, можно сложить в map в C++). Далее переберём пару чисел во втором массиве bi, bj и найдём в нашей структуре данных сумму v наиболее близкую к числу x = sa - sb + 2·(bi + bj) и обновим ответ значением |x - v|. Нужную сумму можно искать бинарным поиском по структуре данных (для map есть функция lower_bound).
Сложность: O((n2 + m2)log(n + m)).
620E - Новогодняя ёлка
Запустим dfs из корня дерева и выпишем вершины в порядке в котором их обойдёт dfs (эта перестановка называется обходом Эйлера). Легко видеть, что поддерево в этой перестановке является подотрезком. Заметим, что цветов всего 60, таким образом, мы можем хранить множество цветов просто как маску двоичных битов в 64-битном типе (*long long* в C++, long в Java). Построим дерево отрезков над Эйлеровым обходом, который поддерживает операцию покраски подотрезка и нахождения маски цветов на подотрезке.
Сложность: O(nlogn).
620F - Ксоры на подотрезке
В этой задаче неудачно были подобраны ограничения в связи с чем некоторые участники сдали решения со сложностью O(n2 + m).
Заметим сначала, что 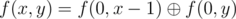 . Значения f(0, x) можно было просто предподсчитать или заметить что в зависимости от остатка числа x по модулю 4 значение функции равно x, 1, x + 1, 0 соответственно.
. Значения f(0, x) можно было просто предподсчитать или заметить что в зависимости от остатка числа x по модулю 4 значение функции равно x, 1, x + 1, 0 соответственно.
Воспользуемся алгоритмом Мо. Разобьём все запросы на  блоков по левому концу. Внутри каждого блока отсортируем запросы по правому концу. Пусть r наибольшая левая граница внутри блока, тогда все левые границы отстоят от r на расстояние не более чем
блоков по левому концу. Внутри каждого блока отсортируем запросы по правому концу. Пусть r наибольшая левая граница внутри блока, тогда все левые границы отстоят от r на расстояние не более чем  , а правые границы идут в порядке неубывания, поэтому их можно двигать по одному (в сумме на один блок мы сделаем не более n передвижений правой границы). Передвигая правую границу, внутри блока для чисел в позициях от r + 1 до текущей правой границы будем поддерживать два бора: первый для значений f(0, x - 1), второй для значений f(0, x), в первом будем поддерживать наименьшее значение x, во втором — наибольшее. Понятно как добавлять число в боры, после добавлений нужно найти наибольшее значение, которое может образовать текущий x для этого будем спускаться по первому бору, поддерживая инвариант того, что в текущем поддереве минимальное значение не больше x, и по возможности ходить по биту отличному от нашего. Аналогичное нужно делать во втором боре, только нужно поддерживать инвариант, что максимальное значение не меньше x. После того как для текущего запроса мы сдвинули правую границу на сколько нужно, нужно пройти от левой границы запроса до r и, не добавляя значения в бор, обновить ответы. Ещё отдельно для каждого запроса в новом (пустом) боре нужно пройти от левой границы до r добавляя значения в бор и обновляя ответ.
, а правые границы идут в порядке неубывания, поэтому их можно двигать по одному (в сумме на один блок мы сделаем не более n передвижений правой границы). Передвигая правую границу, внутри блока для чисел в позициях от r + 1 до текущей правой границы будем поддерживать два бора: первый для значений f(0, x - 1), второй для значений f(0, x), в первом будем поддерживать наименьшее значение x, во втором — наибольшее. Понятно как добавлять число в боры, после добавлений нужно найти наибольшее значение, которое может образовать текущий x для этого будем спускаться по первому бору, поддерживая инвариант того, что в текущем поддереве минимальное значение не больше x, и по возможности ходить по биту отличному от нашего. Аналогичное нужно делать во втором боре, только нужно поддерживать инвариант, что максимальное значение не меньше x. После того как для текущего запроса мы сдвинули правую границу на сколько нужно, нужно пройти от левой границы запроса до r и, не добавляя значения в бор, обновить ответы. Ещё отдельно для каждого запроса в новом (пустом) боре нужно пройти от левой границы до r добавляя значения в бор и обновляя ответ.
С++ solution: в коде 0-й бор соответсвует второму, а 1-й — первому.
Сложность: 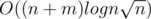 .
.











what about problems E and F ?
E problem can be solved with lazy propagation. The main thing some subtree is represented as list of neighboring elements on dfs list. After that you task is: change elements from interval [L,R] to X, and count how many different elements you have on interval [L,R]. It is clear seg. tree problem and also I think that solution with sqrt decomposition will pass tests.
F problem is pretty hard, if you think about my solution. You can run MO algorithm for queries and after that you can solve task with two tries. Also you should know some performance of xor operation. This solution has complexity O(M sqrt (n) log Ai). Second solution is O(n^2) solution, it is short and interesting. You can read some accepted solution for better understanding that approaches.
For problem E just use the fact that c <=60 then you can make a segment tree where each node contains a bitmask of colours used in this segment and the rest is easy to do.
Done.
Can someone explain E in a better way please ?
I didnt get the part about storing colours as binary bits .
assuming you know how segment tree works, in segment tree: you want to store number of different colors in the range(subtree) covered by a certain node so you can use a bit mask for every node and store that information as following:
for bit_i that represents color_i:
0represents color_i never appeared in the range,1if it appeared one or more times.when updating:
bit-mask_for_node_i = bitmask_of_right_child | bitmask_of_left_childwhen querying: preform binary or
|with all nodes lie in the range you are querying. The answer will be the number of ones in the final mask you get.hope that helps a little bit.
Yeah that helped! Thanks
В задаче С использовал вектор, запихивал в него элементы и, полностью проходя по вектору смотрел есть ли совпадения. После нахождения совпадения обнулял вектор и так далее. Не прошло по времени на 32 тесте. Посмотрел как делают люди и наткнулся на set. set.find, как оказалось, работает в разы быстрее. В чем существенная разница?
Вставка, поиск и удаление в
setработают заО(logn), что естественно в разы быстрее чем полностью пробежаться по массиву заO(n).Is is possible to generalise the problem D for any k?
I don't beleive in it. I was thinking about such option during preparation, but I didn't manage to solve it. Maybe some red coder can help with it ;)
At least it is definitely going to be very hard for large values of k.
Let's take first array with sum S and second array consisting of 0's only. Now it turns out that we want to pick subset of first array and move it to second array in such a way that sum of this subset is as close to S/2 as possible. In case k>=n/2 you have to solve knapsack problem :)
This is good solution for k>=n/2, but I am interested how would you save informations about swaps ? I think that is only possible in cases with really small Ai.
I must think about some harder problems in next period, now I don't have them for next round :D
Complexity will grow for bigger k. nC1+nC2+nC3+...+nCk is the general complexity, AFAIK.
Problem F is really interesting and I think it's a mixture of these two : 86D - Powerful array (MO Algorithm)
282E - Sausage Maximization
Nice :)
Who can tell me why I got TLE on #64, the last test case, in problem E? I have tried so many ways to solve it but they all didn't work... It's just so strange...
I am getting timeout error for problem C. Please Refer this to view my code. I am not able to find the possible solution to this. Please if anyone can indicate what's wrong!
Change temp from vector to set.
Also, check your solution again as it doen't even give correct answer for the sample test case. It gives -1 instead of
1
1 5
I run my code on ideone.com but it gave -1. I run the same code on codeforces custom test section, it gave correct ans. I don't know what caused the error on ideone! And I got timeout error on test case 32 even when I used set instead of vector for temp! Can you suggest any other modifications?
http://www.cplusplus.com/reference/algorithm/find/
http://www.cplusplus.com/reference/set/set/find
Can you see the difference? First algorithm doesn't know what's under the hood (is it vector or set) so it has to go through elements one by one. Second one can use knowledge about the structure to optimize findings and therefore reduce complexity from linear to logarithmic ("default" complexity for search in a set).
Can anyone give me any ideas why this solution is getting TLE:http://codeforces.net/contest/620/submission/17684134? It's pretty much the same idea as listed in the editorial but implemented with set instead of map.
Why is inserting / lower_bound on a set much slower than it is in a map in this particular case?
Can anyone please explain the logic behind this code for F written by waterfall:
include <bits/stdc++.h>
using namespace std;
int n,m; int pref[1<<20]; int a[50013], b[50013]; int dp[50013];
int l[5013], r[5013]; int ans[5013];
int main() { pref[0] = 0; for (int i=1;i<(1<<20);i++) pref[i] = pref[i-1]^i; scanf("%d%d",&n,&m); for (int i=1;i<=n;i++) { scanf("%d",&a[i]); b[i] = pref[a[i]]; } for (int i=0;i<m;i++) scanf("%d%d",&l[i],&r[i]); for (int i=1;i<=n;i++) { memset(dp,0,sizeof dp); for (int j=i;n+1-j;++j) { dp[j] = max(dp[j-1],b[i]^b[j]^min(a[i],a[j])); } for (int j=0;m-j;++j) { if (l[j]<=i) ans[j] = max(ans[j],dp[r[j]]); } } for (int i=0;i<m;i++) printf("%d\n",ans[i]);
}
Can someone explain the logic behind this code for F written by waterfalls
15602452
please tell me anyone, why my soltuion of problem E is give wrong output in first code but it give correct answer in second code (https://codeforces.net/contest/620/my)
You have to also take care of long long,check all 61 bits. I was doing the same mistake.