Komyona_neko's blog

an array A how many indexes (i,j) are there and cumulative sum%K = 0?
By Komyona_neko, history, 9 years ago, In English

Problem Type 1)

Lets say I have an array A[x1,x2,x3,...xN] of size N.

for N = 4 , A = {x1,x2,x3,x4}. [1 based index]

Now,I have to tell how many tuples (i,j) are there such that i<=j and cumulative sum(i,j) is divisible by K.

For example, N = 4

A = { 3,2,5,7} and K = 5.

Now , For this case the answer is 3. as, ( 1,2 ) [cum_sum = 5 ,divisible by K(5)], (3,3) [cum_sum = 5 ,divisible by K(5)] , (1,3) [ cum_sum = 10 ,divisible by K(5)] are such tuples.

I can do this in O(N^2) easily.But how to do this in O(N) or O(N*log(N)) ?

Please give me some problem links based on this (or similar) idea/trick from CodeForces.

  • Vote: I like it
  • +10
  • Vote: I do not like it

Comments Comments (8)
| Write comment?
»
9 years ago, # |
← Rev. 3   Vote: I like it +1 Vote: I do not like it

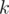Hint: use that is divisible by precisely when .

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Sorry,But that part is just too obvious . Can you give some more hints?

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      Define b0, b1, ..., bi, ..., bn as the sum of the first i elements. Can you give an expression for the sum of the subarray [l, r] for some l ≤ r? If you compare that expression to the hint I gave above, does that give you any ideas?

      Another hint in the previous revision. That should help you understand the solution.

      → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Sum(L, R) = Sum(1..R) — Sum(1..L-1)
So, let F[i] = (a[1] + a[2] + a[3] + ... + a[i]) % K
Then you just do it like this, since to get Sum(L,R) = 0 (mod K), you should have F[L-1] and F[r] equal mod K:
cnt[0] = 1;
for (int i = 1; i <= n; i++) {
ans += cnt[F[i]];
cnt[F[i]]++;
}

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    For example , if my array is {3,2,5,7} Then F{3,0,0,2} cnt{1,0,0,0,0,..........................0} so,in the first iteration ans += cnt[3] = 0 and cnt[3] is now 1.

    in the second iteration ans += cnt[0] = 1 and cnt[0] is now 2.

    in the third iteration ans += cnt[0] = 2 and cnt[0] is now 3.

    in the fourth iteration ans += cnt[2] = 0 and cnt[17] is now 1.

    so,ans = 3.

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I think this the same problem on codeforces ([Link]).(http://codeforces.net/problemset/problem/577/B)

See the tutorial for more help on it.

→ Reply