WalidMasri's blog

Modulo behavior
By WalidMasri, history, 9 years ago, In English

Hello everyone!

i was trying to solve this problem , but the modulo behavior caused me to get WA as a verdict.

When computing the formula 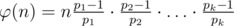, once n is reduced by modulo, the prime divisors (p1,p2... pk) wont remain divisors of n, hence, getting a non-integer result.

MORE Explanation : Given (n%k)/ m, where m is a divisor of n ... if i performed n%k then divided by m, i will get a non-integer result.

What can i do to avoid such problem?

Thanks!

  • Vote: I like it
  • -2
  • Vote: I do not like it

»
9 years ago, # |
  Vote: I like it +6 Vote: I do not like it

You can use the modular multiplicative inverse (109 + 7 is prime).

→ Reply
»
9 years ago, # |
  Vote: I like it +2 Vote: I do not like it

Use this

(a/b)%m = ((a%m)(b^(m-2)%m))%m.

Source

→ Reply