_h_'s blog

Short modular inverse
By _h_, history, 9 years ago, In English

Hi! Modular inverses are used in the solutions to a lot of number theory problems, such as 622F - The Sum of the k-th Powers from the latest educational round. I want to share a one-liner (essentially) that computes modular inverse with the same complexity as the exteneded Euclidean algorithm (a and b are supposed to be positive co-prime integers, and inv(a,b) is the inverse of a modulo b, lying between 1 and b):

long long inv(long long a, long long b){
 return 1<a ? b - inv(b%a,a)*b/a : 1;
}

The idea behind the code is that to compute inv(a,b), we find x such that and 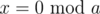, and then return x/a. To find x, we can write x = yb + 1 and solve for y by recursively computing inv(b,a). (Actually inv(b%a,a))

This isn't the fastest method if you're worried about performance, and you will probably get overflow if a*b doesn't fit inside a long long. But I think it's neat.

  • Vote: I like it
  • +173
  • Vote: I do not like it

»
9 years ago, # |
← Rev. 2   Vote: I like it -51 Vote: I do not like it

Another idea for calculating inv( when b is prime ):

int inv(int a,int b){
int ans=1;
int mod=b;
for(b-=2;b;b>>=1 , a*=a , a%=mod)
  if(b&1)
    ans*=a,ans%=mod;
  return ans;
}

This can work because inv(a,b) is a^(b-2) ( b is prime ).

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Shouldn't the code be

b+[1-inv(b%a,a)*b]/a
→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    http://e-maxx.ru/algo/reverse_element


    b%a = b - [b/a]*a

b%a = - [b/a]*a   mod b

// Multiplying both sides by inv(a) and inv(b%a) 

inv(a) = b - [b/a]*inv(b%a) mod b

    Note that here we have taken inverse wrt b in both the case that is a and b%a and not wrt a in case of b%a as mentioned in the blog so shouldn't the code be the following when taken wrt a ??


    x = 1+yb //where y = -inv(b%a,a) since x=0 mod a

inv(a,b)=x/a

inv(a,b) = b+[1-inv(b%a,a)*b]/a  mod b

    What do you say?

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    That's clearer since there's no remainder in the division, and reading it modulo b you just get 1/a. But it's equivalent to what I wrote when a>1, if you do integer division.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      Ok, So you are taking advantage of C++/Cpp rounding towards zero.And since -inv(b%a,a) is negative and [1-inv(b%a,a)*b]/a will be same as -inv(b%a,a)*b/a. When I first saw it, I was confused so I have written the above comment. I got it now. At least I have learned two ways of finding the inverse. Thanks. Learn and Let learn.

      → Reply
»
7 years ago, # |
  Vote: I like it -44 Vote: I do not like it

Another idea for calculating inv( when b is prime ):

int inv(int a,int b){ int ans=1; int mod=b; for(b-=2;b;b>>=1 , a*=a , a%=mod) if(b&1) ans*=a,ans%=mod; return ans; } This can work because inv(a,b) is a^(b-2) ( b is prime ).

→ Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it -16 Vote: I do not like it

So the final code snippet is 

// m must be positive
template<typename T>
static T mod(T a, T m)
{
    a %= m;
    if (a < 0)
        a += m;
    return a;
}

// a must be relatively prime to m
template<typename T>
static T inverse(T a, T m)
{
    a = mod(a, m);
    if (a <= 1)
        return a;
    return mod((1 - inverse(m%a, a) * m)) / a, m);
}
→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +9 Vote: I do not like it

    This code is conceptually clearer. But I don't understand why so many downvotes. Beautiful Codes are MUCH better than 'Shorter' ones!

    → Reply