dcordb's blog

Looking for a closed formula for summation
By dcordb, history, 9 years ago, In English

sin 1 + sin 3 + sin 5 + sin 7 + sin 9 + ...
Any ideas? PD: The angle is in radians.

  • Vote: I like it
  • +1
  • Vote: I do not like it

»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

If you have no clue about a summation, Wolfram Alpha will save your butt. Link

Apperently a closed formular for the first n + 1 elements is: sin(n+1)^2/sin(1). I guess you can prove this formular using induction and a few trigonometrical identities.

→ Reply
»
9 years ago, # |
← Rev. 7   Vote: I like it +22 Vote: I do not like it

sin α = Re(eiα)

→ Reply
»
9 years ago, # |
  Vote: I like it +11 Vote: I do not like it

Lol, I have written my previous post 4 days ago, got 22 upvotes and nobody pointed out, that there should be Im instead of Re :P. Btw even given that equality, I still don't know how to compute that sum : D.

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it +15 Vote: I do not like it

    You have a sum of geometric progression inside Im, you may calculate its sum in O(1) as some fraction and explicitly express its imaginary part by carefully dividing numerator by the denominator.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +11 Vote: I do not like it

      OK, that geometric progression is what I had in my mind when I was writing first post, but somehow I got stuck when computing imaginary part of [tex_crapped_on_cf]\frac{e^{(2n+1)i} — e^i}{e^{2i} — 1}[\tex_crapped_on_cf], but of course it can be done.

      → Reply
»
9 years ago, # |
  Vote: I like it +53 Vote: I do not like it

It is good idea to multiply this by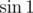 or 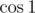(because, for example, 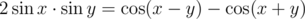and there will be a lot of summands that "kill" each other, it is general way to simplify such sums) to get telescopic series, let's multiply (for example, 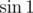, it works better in this case):

So, .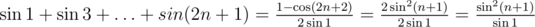

→ Reply