С подачи e-maxx подзагрузился доказательством факта d(n) = o(n^ε). Факт, вроде бы, не очень известный и весьма содержательный с теоретической точки зрения (но не с практической, как будет видно дальше).

Ниже вы можете ознакомиться с моим вариантом доказательства. За комментарии и (тьфу-тьфу) указания ошибок буду благодарен. Если что-то непонятно, готов объяснить.

У меня при просмотре из Firefox 10 наблюдается такой спецэффект: при отображении записи рендерятся не все формулы, причем если обновлять страницу, то рендерится другое подмножество формул. =) Надеюсь, это поправят, а пока дочитав до места, где должна быть формула, надо обновлять, пока она не появится. =)

Итак, что же мы хотим доказать? Для любого ε > 0 верно, что 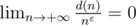, где d(n) — число делителей числа n.

Сперва заметим, что достаточно доказать, что 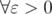d(n) = O(n^ε), т.е. существует положительное C, зависящее от ε, такое что d(n) ≤ Cn^ε. Действительно, пускай это так. Тогда d(n) ≤ Cn^ε / 2 = o(n^ε).

Приступим к доказательству d(n) = O(n^ε). Далее ε считаем фиксированным.

Пусть n = p₁^b₁... p_k^b_k, где все p_i — различные простые числа и все b_i натуральные (т.е. это каноническое разложение числа на степени простых). Тогда известно, что d(n) = (b₁ + 1)... (b_k + 1). Поделим d(n) на n^ε:

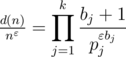
Мы доказываем, что это отношение не превосходит некоторого C.

Рассмотрим вспомогательную функцию 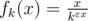, где k — некоторое положительное число, а ε ровно тот, что мы фиксировали (вид этой функции очень похож на вид одного множителя из последнего произведения). По ее виду сразу понятно, что если x стремится к 0 или к  + ∞, то f_k(x) стремится к 0. Значит, в некоторой положительной точке она достигает максимума (таких точек может быть несколько), и в ней производная равна нулю. Для удобства мы будем дифференцировать логарифм f_k(x), поскольку у него точка (или точки) максимума там же, где и у f_k(x):

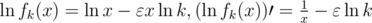
В точке максимума производная равна нулю, т.е. 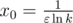— глобальный максимум (т.к. других нулей у производной нет).

В любой другой точке x

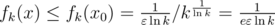
Теперь применим доказанное к нашему отношению:

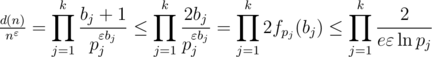
Из последней формулы видно, что если p_j больше e^2 / eε, то соответствующий член произведения будет меньше 1, поэтому, исходя из того, что все p_j различны:

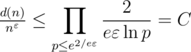
, где C зависит только от ε.

UPD: А вот еще прикол с этим доказательством, сам только что случайно наткнулся. Можно в качестве функции f_k(x) взять как раз элемент произведения 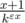. Тогда при применении того же метода построения верхней оценки получится, что 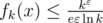, что стремится к бесконечности с ростом k, и потому не годится для оценки произведения. Каково? =)