Problems ABCG will be described better soon.
problem A — watch out for test like "1 1 1 2 2 2 2 3 3 3". It shows that it's not enough to sort number and check three neighbouring elements. You must remove repetitions. The easier solution is to write 3 for-loops, without any sorting. Do you see how?
problem B — you should generate all 6n possible starting strings and for each of them check whether you will get "a" at the end. Remember that you should check two first letters, not last ones (there were many questions about it).
653C - Bear and Up-Down — Let's call an index i bad if the given condition about ti and ti + 1 doesn't hold true. We are given a sequence that has at least one bad place and we should count ways to swap two elements to fix all bad places (and not create new bad places). The shortest (so, maybe easiest) solution doesn't use this fact but one can notice that for more than 4 bad places the answer is 0 because swapping ti and tj can affect only indices i - 1, i, j - 1, j.
With one iteration over the given sequence we can find and count all bad places. Let x denote index of the first bad place (or index of some other bad place, it's not important). We must swap tx or tx - 1 with something because otherwise x would still be bad. Thus, it's enough to consider O(n) swaps ~-- for tx and for tx - 1 iterate over index of the second element to swap (note that "the second element" doesn't have to be bad and samples show it). For each of O(n) swaps we can do the following (let i and j denote chosen two indices):
- Count bad places among four indices: i - 1, i, j - 1, j. If it turns out that these all not all initial bad places then we don't have to consider this swap — because some bad place will still exist anyway.
- Swap ti and tj.
- Check if there is some bad place among four indices: i - 1, i, j - 1, j. If not then we found a correct way.
- Swap ti and tj again, to get an initial sequence.
Be careful not to count the same pair of indices twice. In the solution above it's possible to count twice a pair of indices (x - 1, x) (where x was defined in the paragraph above). So, add some if or do it more brutally — create a set of pairs and store sorted pairs of indices there.
TODO — add codes.
CHALLENGE — can you solve this problem if the initial sequence is already nice (if it doesn't have bad places)?
653D - Delivery Bears — invented and prepared by Lewin, also the editorial.
Java code: 16825205
C++ code solving also the harder version: 16825257
Let's transform this into a flow problem. Here, we transform "weight" into "flow", and each "bear" becomes a "path".
Suppose we just want to find the answer for a single x. We can do this binary search on the flow for each path. To check if a particular flow of F is possible, reduce the capacity of each edge from ci to 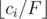 . Then, check if the max flow in this graph is at least x. The final answer is then x multiplied by the flow value that we found.
. Then, check if the max flow in this graph is at least x. The final answer is then x multiplied by the flow value that we found.
MUCH HARDER VERSION — you are also given an integer k (1 ≤ k ≤ 104) and your task is to find the answer for x paths, for x + 1 paths, ..., and for x + k - 1 paths. There should be k real values on the output.
653E - Bear and Forgotten Tree 2
C++ code: 16826422
You are given a big graph with some edges forbidden, and the required degree of vertex 1. We should check whether there exists a spanning tree. Let's first forget about the condition about the degree of vertex 1. The known fact: a spanning tree exists if and only if the graph is connected (spend some time on this fact if it's not obvious for you). So, let's check if the given graph is connected. We will do it with DFS.
We can't run standard DFS because there are maybe O(n2) edges (note that the input contains forbidden edges, and there may be many more allowed edges then). We should modify it by adding a set or list of unvisited vertices s. When we are at vertex a we can't check all edges adjacent to a and instead let's iterate over possible candidates for adjacent unvisited vertices (iterate over s). For each b in s we should check whether a and b are connected by a forbidden edge (you can store input edges in a set of pairs or in a similar structure). If they are connected by a forbidden edge then nothing happens (but for each input edge it can happen only twice, for each end of edge, thus O(m) in total), and otherwise we get a new vertex. The complexity is 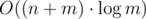 where
where 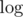 is from using set of forbidden edges.
is from using set of forbidden edges.
Now we will check for what degree of vertex 1 we can build a tree. We again consider a graph with n vertices and m forbidden edges. We will first find out what is the minimum possible degree of vertex 1 in some spanning tree. After removing vertex 1 we would get some connected components and in the initial graph they could be connected to each other only with edges to vertex 1. With the described DFS we can find c (1 ≤ c ≤ n - 1) — the number of created connected components. Vertex 1 must be adjacent to at least one vertex in each of c components. And it would be enough to get some tree because in each component there is some spanning tree — together with edges to vertex 1 they give us one big spanning tree with n vertices (we assume that the initial graph is connected).
And the maximum degree of vertex 1 is equal to the number of allowed edges adjacent to this vertex. It's because more and more edges from vertex 1 can only help us (think why). It will be still possible to add some edges in c components to get one big spanning tree.
So, what is the algorithm? Run the described DFS to check if the graph is connected (if not then print "NO"). Remove vertex 1 and count connected components (e.g. starting DFS's from former neighbours of vertex 1). Also, simply count d — the number of allowed edges adjacent to vertex 1. If the required degree k is between c and d inclusive then print "YES", and otherwise print "NO".
653F - Paper task — invented and prepared by k790alex, also the editorial.
Java code (modify-SA-solution): 16821422
C++ code (compressing-solution): 16826803
There are two solutions. The first and more common solution required understanding how do SA (suffix array) and LCP (longest common prefix) work. The second processed the input string first and then run SA+LCP like a blackbox, without modifying or caring about those algorithms.
Modify-SA-solution — The main idea is to modify the algorithm for computing the number of distinct substrings using SA + LCP.
Let query(L, R) denote the number of well formed prefixes of substring(L, R). For example, for substring(L, R) = "(())()(" we would have query(L, R) = 2 because we count (()) oraz (())().
How to be able to get query(L, R) fast? You can treat the opening bracket as + 1 and the ending bracket as - 1. Then you are interested in the number of intervals starting in L, ending not after R, with sum on the interval equal to zero. Additionally, the sum from L to any earlier right end can't be less than zero. Maybe you will need some preprocessing here, maybe binary search, maybe segment trees. It's an exercise for you.
We can iterate over suffix array values and for each suffix we add query(suffix, N) - query(suffix, suffix + LCP[suffix] - 1) to the answer. In other words we count the number of well formed substrings in the current suffix and subtract the ones we counted in the previous step.
The complexity is  but you could get AC with very fast solution with extra
but you could get AC with very fast solution with extra 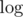 .
.
Compressing-solution — I will slowly compress the input string, changing small well-formed substrings to some new characters (in my code they are represented by integer numbers, not by letters). Let's take a look at the example: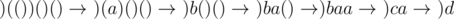
or equivalently: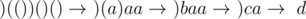
Whenever I have a maximum (not possible to expand) substring with single letters only, without any brackets, then I add this substring to some global list of strings. At the end I will count distinct substrings in the found list of strings (using SA+LCP). In the example above I would first add a string "a" and later I would add "baa". Note that each letter represents some well formed substring, e.g. 'b' represents (()) here.
I must make sure that the same substrings will be compressed to the same letters. To do it, I always move from left to right, and I use trie with map (two know what to get from some two letters).
problem G — you can consider each prime number separately. Can you find the answer if there are only 1's and 2's in the input? It may be hard to try to iterate over possible placements of the median. Maybe it's better to think how many numbers we will change from 2^p to 2^{p+1}.











I strongly believe suffix automaton to be the most convenient suffix structure to use in almost all cases. 16808872
But anyway, second solution is very interesting! But can you please describe it in more details? Maybe provide a full algorithm on example of some short string.
Can you describe your solution?
Sure. Each state in suffix automaton corresponds to some set of strings which are suffixes of each other and can be found as substring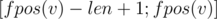 where
where 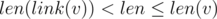 and
and 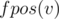 is the first position where these strings can be found.
is the first position where these strings can be found.
Now for each state we should calculate how many there is such suitable substrings. To do this you can keep in sparse table for each position in string where there is character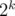 noncontracting correct sequences.
noncontracting correct sequences.
)how many letters we should step to the left from this position to get the concatenation of exactlyIf we maintain that, now we can just do some kind of binary search to get the answer for each state (more precisely we can do binary search on sparse table to count f(x) — how many correct sequences we can concatenate starting at some position without extending length . Then the answer for state is
. Then the answer for state is 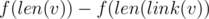 ). Since sets of substrings in all state pairwise non-intersecting, we can just sum all these values.
). Since sets of substrings in all state pairwise non-intersecting, we can just sum all these values.
By the way, you probably didn't know about it, but there was similar problem from tourist in Petrozavodsk Camp 2013: link.
Could you explain the term: "non-contracting" correct sequences. That would be really helpful.
This seems to be a bad problem to advocate suffix automaton usage, especially because that solution looks almost identical to the one with suffix arrays.
I should really get to learn automata sometime, but it seems to be a really magical structure at times.
I would appreciate a more detailed editorial for problem G.
My solution: Consider only one prime p. Let sequence of exponents at p in a1, a2, ..., an be e1 ≤ e2, ... ≤ en.
In one move we can increase some
Unable to parse markup [type=CF_TEX]
by 1 or decrease it by 1. It is well known that, in order to minimize number of moves, we should change each number to the median.In fact the number of moves needed is - e1 - e2 - ... - e[n / 2] + e[(n + 1) / 2] + ... + en. For example when n = 2 it is e2 - e1, when n = 3 it is e3 - e1, when n = 4 it is e4 + e3 - e2 - e1, etc.
Now we want consider all subsets of e. We will obtain sum of ei with some coefficients. For example when n = 3 we will get e3 - e1 for subset (e3, e1), e3 - e2 for subset (e3, e2), e2 - e1 for subset (e2, e1) and e3 - e1 for subset (e3, e2, e1). In total 3e3 - 3e1. For example when n = 4 we will get in total - 7e1 - 3e2 + 3e3 + 7e4, etc.
The general formula for this will be:
We precompute those coefficients, and its prefix sums. There are not so many ($\leq 20$) possible values of ei. So we can compute the above sum very fast.
We do the same thing for each prime and sum up.
How do you derive 'the general formula'? I cannot see where does it come from..
I didn't prove it. I wrote the brute-force up to n = 10, and then I realized that differences between consecutive coefficients are just newton symbols.
In fact for every element you need to know how many times it appears in the "left" part of a subsequence, and how many times it appears in the "right" part. For element ek, if it's in the "left" part of a subsequence, it means this sequence has less elements in e1...ek - 1 than ek + 1...en. Consider following polynomial: (1 + x)k - 1(1 + x - 1)n - k = (1 + x)n - 1 / xn - k, number of sequences equals to the sum of coefficients of non-positive degree x power.
Beautiful. Thanks!
For the less polynomially inclined:
You want to know in how many ways we can pick some elements from the L left ones and some from the R right ones, such that we pick more elements from the right than from the left.
Let's suppose we pick exactly k more from the right part, so that we pick l from the left part and l+k from the right. If you flip the elements in the right (so that unpicked become picked and vice-versa), the total number of elements picked becomes l+(R-l-k) = R-k. In this way, we find a bijection between number of ways of choosing exactly k more from the right part and choosing R-k elements from all elements, but the second one is easy to count: it's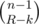 .
.
To get our final answer just sum for all possible k.
This is the mostest bestest awesomest thing I have ever seen
+99999999999999999999999999999
I posted my solution below.
Thanks for the very nice problem set! Sadly I made some small mistakes on D and E, but DEFG were all interesting problems (since I was able to solve all of them after a few hours of thinking :) ).
Here's my solution for G: 16825992
Disclaimer: There might be some off-by-one errors in the formulas at the end, because my drafts used zero-based indices.
First, factor all ti, and for each prime p, let mp, e be the number of ti with exactly e factors p. Now, we solve the problem for a single prime p. The final answer will be the sum of the answers for all primes. When we are given a set of numbers with (sorted) exponents E = {e1, ..., ek}, with k odd, the fastest way to make all exponents equal is to move them towards the median, e(k + 1) / 2. If k is even, we can choose any value between ek / 2 and ek / 2 + 1, but I will assume we always choose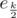 . Thus, let m = k / 2 be the median. Now, it would be nice if we could determine the total cost of making the median equal to em. We do this by calculating the average cost of \emph{moving} all ei to em over all subsets of E containing em.
. Thus, let m = k / 2 be the median. Now, it would be nice if we could determine the total cost of making the median equal to em. We do this by calculating the average cost of \emph{moving} all ei to em over all subsets of E containing em.
In my first attempt, I made separate calculations for even and odd subset sizes, but after seeing the final expression, it turns out we can use a nice combinatorial argument:
Lets devide E in two parts: El = {e1, ..., em} and Eh = {em + 1, ..., ek}. If we choose i elements from both El and Eh (call these sets A and B), we know that em is an optimal target. If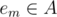 , we have a good subset
, we have a good subset 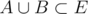 , with an even number of elements. If
, with an even number of elements. If 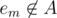 , we can add it to A, to obtain the subset
, we can add it to A, to obtain the subset 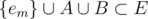 . This has an odd number of elements. In this way, we enumerate all subsets of E containing em as a median.
. This has an odd number of elements. In this way, we enumerate all subsets of E containing em as a median.
Next, we calculate the distances we have to move all elements to em. Since we iterate over all subsets, we can use an expected value argument to get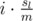 for average total distance we have to move the elements of A to em. Here, sl is the value of
for average total distance we have to move the elements of A to em. Here, sl is the value of
A similar expression holds for the elements of B, which will be left as an exercise for the reader ;)
Using this, we obtain the following formula for the total distance we have to move elements in A to em:
Using a combinatorial argument,
Thus, for every prime, we have to evaluate
where sl is the total distance from the current element to all previous elements. In fact, it is sufficient if we only do this calculation once, and precalculate the changes in sl for every prime p. Have a look at the code linked above for details (or rather, code), as this is a bit tedious to explain.
The sum of the moves from the right can be done in a similar way, but requires a bit more care in the precalculation of the differences.
The last formula has a flaw: it should be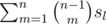
You're right; I fixed the mistake.
In the editorial for problem E, you describe printing "YES" and "NO", but the problem statement says you should print "possible" or "impossible" (trivial things).
In problems such as D where you binary search on doubles, what is the best way to avoid both TLE and wrong answer? I had the line
while(high - low >= EPS)and had to change the value of EPS multiple times to get accepted.You can iterate a fixed number of times, generally 80/100 times is enough.
I saw that most submissions used this. However, I can't understand why this is more effective; it seems like it has the same chance to time out or give wrong answer as
while(high - low >= EPS).You are iterating a constant number of times, choosing a good constant will ensure a low error and is easier to play with it, with EPS you are doing a dynamic number of iterations and is easier to get TLE in this way.
Using a fixed error tolerance with values that can take multiple orders of magnitude is bad.
A loop of the form you describe might not even terminate (becoming an infinite loop) if eps is small enough compared to the double precision. And if eps is too large you get WA. Fixed number of iterations just works reasonably in every case.
Iterating a fixed number of times is better, but if you really want to play with EPS I suggest you use long doubles instead of doubles — they have much better precision.
I would like to share my solution from the official finals to 653E-Bear and Forgotten Tree 2, because I find it rather interesting.
First, I wanted to compute the connected components if we exclude vertex 1. In order to do this I repeatedly chose a non-visited vertex x and "expanded" its connected component starting from x. I did this with a BFS, in the usual way, by considering all the non-forbidden neighbors and, if they were not visited before, I added them to the queue. The trick here was to choose a threshold T, which is slightly more than sqrt(M). Then, once T nodes were considered in the BFS, we stop (i.e. we don't necessarily compute the connected component fully). During the BFS's I might encounter vertices which were visited as part of some other component, but were not expanded further due to the threshold. For these cases I used Union-Find, in order to merge the newly expanded component to other components which were not fully expanded because of the chosen threshold.
In the end we get a number of connected components. Any component with less than T vertices was fully expanded (thus, it's a full connected component — no more vertices can be added to it). Any components with >= T vertices can actually be merged in a single component. Why? It's easy to see. Let's assume that we have two such components, one with A vertices, the other with B vertices, with both A and B >= T. There are A * B possible edges between these two components. But, since T > sqrt(M), we have A*B>M. Thus, there exists at least one pair of vertices, one from the first component, the other from the second component, such that the edge between them is not forbidden.
After this we just need to check that:
The overall time complexity is dominated by O(N * sqrt(M) * Union-Find time complexity). I implemented Union-Find with path compression and union-by-size. During the algorithm there can be at most N-2 successful Unions, but many more Finds. Thus, path compression was very useful here to flatten the Union-Find trees and make the complexity of each Find very close to O(1).
Here's another method for finding the connected components: let Si be the set of vertices adjacent to i in the given graph. We know that for i = 2, 3, ... , n, all vertices not in Si belong to the same connected component. This is sufficient information to break the graph into connected components. It's easy to see that if there exists some k which is not in either Si or Sj, we can replace Si and Sj by instead without losing/changing any information. The second observation is that if |Si| < n / 2 and |Sj| < n / 2, there must always exist such a k. So we can replace all sets with size < n / 2 with their intersection instead (the sum of the sizes of the sets is 2m, so this part takes O(m)). It is easy to solve the remaining part in
instead without losing/changing any information. The second observation is that if |Si| < n / 2 and |Sj| < n / 2, there must always exist such a k. So we can replace all sets with size < n / 2 with their intersection instead (the sum of the sizes of the sets is 2m, so this part takes O(m)). It is easy to solve the remaining part in 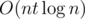 where t is the number of sets remaining (maintain a dsu; iterate from i=2 to n, for each i, for each set not containing i merge it with the previous set not containing i (if any)). This is actually
where t is the number of sets remaining (maintain a dsu; iterate from i=2 to n, for each i, for each set not containing i merge it with the previous set not containing i (if any)). This is actually 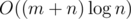 at most: there cannot be more than 4m / n vertices with degree > n / 2 (otherwise the sum would be more than 2m), so t ≤ 4m / n + 1.
at most: there cannot be more than 4m / n vertices with degree > n / 2 (otherwise the sum would be more than 2m), so t ≤ 4m / n + 1.
My solution for F is a combination of compression and generalized suffix automaton :) And it's like 20 lines of code besides standard SA implementation.
http://codeforces.net/contest/653/submission/16834751
Explanation added:
Basically we enumerate simple correct bracket subsequences as they are encountered and they are letters in the suffix automaton we build. Initially we have only one
(), that is empty inside and has index 0.If the bracket opens, we go to the next stack level. If one closes — the current level is enclosed in the pair of brackets, so we get a letter. In order to know its index, we add the string representing current level to the automaton and look at the endIndex of the state (this is non-standard field, but very easy to maintain).
For example, we can get
() = 0,(()) = (0) = 1,((())()()) = (100) = 2.What we need to count is actually the number of different substrings of everything we added to the automaton. Since we can have open brackets without corresponding closed ones, we also add everything left in the stack before printing the answer.
I am so slow, we can just use state index as a letter index. So we have an automaton with alphabet equal to its set of states :D
http://codeforces.net/contest/653/submission/16862065
The idea is similar to Errichto solution and your code is much shorter.
Is interesting the way you applied suffix automaton to do it, I definitely will learn it someday.
In B I found better solution than greedy one. My idea was to go from the end to beginning : let dp[i][j] is number of correct sequences with length i, which ends by letter j. dp[0][a] = 1. Conversion is dp[i][j] += dp[i — 1][k] if we have request like 'jx k'. Time complexity is O(Q * S * N), where s is number of different letters.
P.S. sorry for poor english.
The beginning of dp should be: dp[2][x]= number of operations that convert to letter x.
And I believe time complexity is O(n × q), since you should check all letters from a to f, which means S = 6.
My code: 17198645
This problem is based on same idea :)
https://www.spoj.com/problems/MAIN113/
Can anyone explain the solution for problem C in more detail ?
I solved this way:
First mark which [a, b = a + 1] intervals are good and which are bad.
Bad interval if:
even x and T[a] > = T[b]
odd x and T[a] < = T[b]
otherwise good interval
If there are 5 or more bad intervals, then it is impossible to reach a nice sequence by making a single swap because a swap can fix at most the four intervals the two swapped values affect. So this way we discarded the majority of the cases in only O(N)
Now we need to deal with the cases there are four or less bad intervals
We can bruteforce the only swap we can make with all the values that are part of the bad intervals (of course a solution would swap one of these values). We'll test to swap all these values with each of the ith members of the array, and if any of them make a nice array then we've find the solution, otherwise there is no solution because the wrong intervals are not affected)
Beautiful. But there is a technical problem, how can we test if a swap chance make a nice array? We could do this on O(N) by iterating the array but because we are already under an O(N) testing all the items to swap then this would make a time limit O(N2)
We need to get if the array is nice in O(1) and the trick is simple, we need to note that when we make the swap we only affect the status of the four intervals that the two swapped values take part.
So we can make a sum range query of the unmodified values by computing before solving the problem for each value of the array How many errors are between the items [0,x], and this way we can query the errors of any range of values [a, b] = p[b] - p[a - 1]. And we can sum the errors of the intervals that are affected by the swap to the queries that make all the unmodified values in O(1).
And that's all! In my case I used a set to avoid counting two times the same swap solution but I think this can be avoided somewhat.
16822666
Good Luck
In problem D , I tried implementing Edmonds–Karp algorithm , but I got TLE. ( Here is my submission if interested: http://codeforces.net/contest/653/submission/16878976 ) Is it possible to use that algorithm, or it will be too slow, and I should use Dinic, as shown in example codes?
Update: finally I could make it work, and I got AC.
Yes, Dinic is much better in this case because it is working in n*n*m, but Edmonds-Karp working in n*m*m. Also you must bin search on answer(it is 100-200 operations), so in the worst case Edmonds-Karp algorithm will done 200*50*500*500=2,5*(10^9) operations and Dinic will done 200*50*50*500=2,5*(10^8); So Dinic will run ten times faster.
Why are you multiplying by 200? log2(10^6)~=20 So both implementations are ten times faster then you said and my solution using Edmonds-Karp got 30ms.
I found a week tests for problem D. I solve it via Ford Fulkerson and forget push revers flow but get AC.
My submission: http://codeforces.net/contest/653/submission/16901974
for problem E in java i got tle in 6th case in which i have used hashset to store remaining element and when i changed it to TreeSet it has been accepted why? i dont understand. can anybody help me with this.Thanks Accepted:http://www.codeforces.com/contest/653/submission/16919180 Tle:http://www.codeforces.com/contest/653/submission/16919201
In your dfs method you are iterating over values of 'rem', iterating over a HashSet is too slow due to HashSet internal structure, you can try LinkedHashSet instead which is better for iterating.
http://codeforces.net/contest/653/submission/19413553
Adjacency can handle Problem B in a very decent time complexity. Time complexity: O(logn) for quick power algorithm.
For problem B we have a test case as
We can have three strings as
But the answer is 2 How?
there is no 'bc' in the test case, mate