Hello everyone,
Some days ago we had an annual programming contest in Samara, and yet again we copy it into Codeforces Gyms. The gym contest takes place on Sunday, 17 April, at 11:00 MSK. Site clist.by says that there are no intersections with something important that day.
Previously, it was a team contest, but this year we decided to make it personal. So we ask everyone to participate solo. This is how the results will be the most adequate.
And as usual,
The list of our previous contests











Great :D
I really like the previous Samara contests :)
Islam-Emam Rashwan MoHaMe_KhaLed amrsaeedhosny zoma Andrew_Emad
No, it's Codeforces not Facebook. Tagging your friends won't appear for them in notifications.
But what if it did actually work?
I mean instead of messaging five different people on CF about the same contest, wouldn't it be nice and convenient if we could just tag them and they receive notification or something?
I don't think that tourist will like it , as he's going to be fully spammed.
Not if only the people in friend list of tourist are allowed to tag him ;)
A person should get notified only if his/her friend tags him/her.
PS — BTW I had no idea you replied to my comment till I revisited this page just now. :P May be a person should get notified if someone replies to his/her comment?
You will get notified through your email. I think it would be more convenient to get notified here rather than in email.
how to solve E?
The one half of the figure can be translated into the other by some linear transformation. Let's iterate over all possible transformations. There are three important parameters of a transformation:
1) translation by X axis from -50 to 50 and by Y axis from -50 to 50
2) rotation on 0/90/180/270 degrees
3) mirroring — yes or no
This gives us a total of 101x101x4x2 transformations.
For each transformation, let's consider an oriented graph, where vertices are cells of the figure and edge (u,v) means that cell u is transformed to cell v by this transformation.
Our transformations are invertable, so there are at most one incoming and at most one outcoming edge for each vertex.
Because of this, the graph is formed by cycles and chains. If all cycles and chains are of even length, we can color the graph vertices in red and blue so that no edge connects vertices of same color. The red and blue parts of graph would mean the two parts of the input figure.
If for each transformation there is at least one cycle or chain of odd length, the answer is Impossible.
I had a slightly different approach. I let the top-left point of the figure be a point in the A figure, and brute forced over the corresponding point in the B figure, as well as the rotation and flipping. Then, on the remaining points, I constructed a 2-SAT instance with a variable for each cell and where being part of A is equivalent to being set to true and being part of B is false. if a given cell was a part of A, its corresponding cell (the cell with the same, possibly rotated/flipped, offset relative to the top-left corner of figure B) must be a part of B, and vice versa.
Here is my game, on which the Bisection problem from this contest was based.
Can anyone show, how to solve "L"-Chess Match.
We want to understand are there any permutations
AofaandBofbsuch that the number of positionsiwithA[i]>B[i]is more thann / 2.Let's find the worst case(when the number
kof such positions is the greatest possible) . It is easy to see in this case some of thekleast numbers ofbare less than someknumbers ofa. So let's findkgreedily step by step. Every step needs to find the least numberxinb, and the least numberyinawhich satisfies a conditiony > x. So k = the number of times when you can find suchyFor doing this you may use set or simple sorting
Just do this algorithm with
(a, b)and(b, a)and print the answerYour text to link here...
I compared the
n/2 + 1smallest elements ofAwith the same number of the largest elements ofB, element-wise (0th with 0th, 1st with 1st, etc.).Could anyone tell me how to solve pro H and pro J? Thanks in advance.
Answer is YES if there is cycle in graph or cell with three or four free neighbours.
Is that an arbitrary cycle?
Yes. Code
Oh, it's really amazing :D. Thank you so much :D.
What should be the output of this test case?? and why
4 5
#####
...#.
...#2
1..#.
It's incorrect test. From statement: "From every free cell it's possible to reach every other free cell by moving only through the cells sharing a side."
oh.. Thanks :)
Solution H
For size i we need to find i-th smallest index of friend among friends going to the party of that size.
It can be done next way: iterate over party size from 1 to N. For size i:
Segment tree can perform these operations with O(logN) complexity, it is enough in this problem.
C++ has a cheating data structure — a set with methods order_of_key() and find_by_order(). Link
(if you didn't know the cheat above) In this problem such data structure can be emulated by 2 sets, one of which stores the lowest k values, and the other one stores the rest values. Since the find_by_order(k) calls are not arbitrary — parameter k is increasing — it's easy to maintain this data structure by moving the smallest elements from the second set to the first one.
Of course, segment tree or (fenwick tree + binary search) also work.
H. Let's have a look at some K. Let's create array c[] with c[i] = 1 if a[i] <= k <= b[i]. Then the answer for a query with group's size = K is the K-th index i with c[i] = 1 or -1 if there is no K ones in array. For more fast processing the queries(finding k-th positions/updating the cell) we can build a segment tree over the array c
Now let's iterate over K from 1 to n. Before answering for a query K we must change c[i] to 1 for every position with a[i] == K (in segment tree, of course). After answering for a query K we also must change c[i] to 0 for every position i with b[i] == K. As you can see, implementation these operations keeps real array c in some moment K in our segment tree.
Maybe code is the best explanation
Another solution H.
Let's build data structure, that can perform next operations on array 'a':
Segment tree can perform all these operations with O(logN) or O(sqrtN) complexity, it is enough in this problem.
Idea of solution:
Initialize out data structure with values (-1, -2, -3, ..., -n) for indexes 1..n.
Iterate over friends from 1 to N, for friend with index i do:
Also another
is parallel binary search. For every k = 1... N, set initial lower and upper bound as 1 and N. Then iterate over the array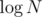 times, and using an auxiliary data structure like a BIT narrow the range for each query down as you arrive at its mid-point. This is O(N × log2N), read more about the technique here
times, and using an auxiliary data structure like a BIT narrow the range for each query down as you arrive at its mid-point. This is O(N × log2N), read more about the technique here
Can anyone tell me how to solve problem F ?
p1 is moving with velocity vector v1 and p2 is moving with velocity vector v2. Relative to p1, p2 starts at p2 — p1, and is moving with velocity vector v2 — v1, Then, you want the closest point on this ray to the origin, which is almost the same as the point-line segment distance problem and can be solved using a very similar formula.
Thank you :D
Ternary search also works well, and is easier to understand, I think.
Function for square of distance between points at the time 't' is a*t^2 + b*t + c. I don't think, that it is harder to find minimum of that function: max(0, -b/2a) — than understand and implement your solution correctly and without problems with precision.
He meant this one: 17360287
But the solution by mkirsche (comment) is the most reliable. There are problems where numerical solutions don't work.
how to solve I and M ?
We need to make observation that function of different characters in suffix of any string is increasing with length of suffix increasing (in other words, it's monotonic).
Then, let dp[i] be the optimal answer for i-th prefix of string, dp[0] = 0. Let's imagine we're standing at the end of i-th prefix of string. Now, we need to find such positions l and r that l is the leftest position at which substring [l; i] has exactly k different characters and r is the rightest position at which substring [r; i] has exactly k different characters. Now, dp[i] = min(dp[l-1]..dp[r-1]), because all substrings from [l; i] to [r; i] are good (due to function mentioned earlier being monotonic), and we can concatenate any of them with shorter prefix. You can get min(dp[l-1]..dp[r-1]) with segment tree. Now we only need to find such l and r. You can do it using two pointers or binary search with some data structure that can answer queries like "how many different characters there are on segment [l..r]". For example, it can be sparse table with bitmasks of length 26 to get O(1) time for query.
Total complexity is O(N log N).
Sorry for bad English :)
thank you :D
How to solve Problem A-Treasure Island??
Got Wrong Answer in Case No-9. I use dp and dfs.
My code is here-17709718
You can replace '?' with '.' or '#'. But you replace '?' only with '.'
My idea is-
If all land land position is connected and can be reached from any land position then others '?' mark can be replaced with either '.' or '#'.
If all land position is not connected then we can replace '?' mark to '.' so that all land mark become connected.
If we need every '?' mark to change in '.' mark to connect all land mark then we have a valid solution and If there remain some extra '?' mark that can be replaced with either '#' or '.' so this situation is ambiguous.
And if we can't make all land mark connected after using all '?' mark then this situation is impossible.
I am not sure my idea is correct or not. Please Give me some hints/idea or source code.
You can run bfs\dfs from all '.' and mark all reachable '?'. If '.' are not connected then answer is "Impossible" else check for all marked '?': if you replace this '?' with '#' and all '.' are connected then answer is "Ambiguous" (you can replace this '?' with '.' or '#' so that '.' are connected).
my source
how to solve D ?
It can be solved by processing cities, ordered by descending their populations.
You can use map for storing already processed cities by their coordinates.On each step you simply look and compare two cities by their distances to city, processing on this step: nearest from left and nearest from right.
How to solve I?
How to solve problem I?
Sort tasks by deadline. Not by "deadline — time" or any other shit.
Then process them in this order. If a task requires some dependencies, do them. If you can't do some task in time, output "NO".
thank a lot, I was able to solve now.
Why is this greedy strategy correct?